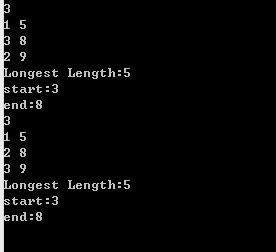
题目:
X轴上有N条线段,每条线段包括1个起点和终点。线段的重叠是这样来算的,[10 20]和[12 25]的重叠部分为[12 20]。
给出N条线段的起点和终点,从中选出2条线段,这两条线段的重叠部分是最长的。输出这个最长的距离。如果没有重叠,输出0。
思路:
1、暴力计算
依次计算两两线段之间的重叠长度,但复杂度太高
2、动态规划
假设S[n]表示n条线段中最长重叠距离,最长重叠距离只与两条线段有关,那么考虑两种情况:
1. 最长重叠距离与第n条线段无关,则最长重叠距离存在于前n-1条线段中,即S[n]=S[n-1];
2. 最长重叠距离与第n条线段有关,则最长重叠距离为第n条线段与前面n-1条线段中的最大重叠距离者,S[n]=max(overlap(segment[n],segment[i])), i=1....n-1
因此得到状态转移方程:
S[n]=0; n<=1
S[2]=overlap(segment[0],segment[1])
S[n]=max(S[n-1],max(overlap(segment[n],segment[i])))
代码:
动态规划:
#include
#include
#include
using namespace std;
typedef struct{
int start;
int end;
}segment;
bool isShorter(const segment &s1,const segment &s2);
int commonSegment(const segment &seg_a,const segment &seg_b);
int findLongestSegment(const vector &segments,int size);
int main()
{
int n;
int start,end;
while(cin>>n){
vector segments(n);
for(int i=0;i>start && cin>>end){
segments[i].start=start;
segments[i].end=end;
}
}
// sort by segment.end
// sort(segments.begin(),segments.end(),isShorter);
int maxLen;
maxLen=findLongestSegment(segments,n);
cout<<"Longest Length:"<seg_b.end){
commonSeg.start=0;
commonSeg.end=0;
}
else{
commonSeg.start=max(seg_a.start,seg_b.start);
commonSeg.end=min(seg_a.end,seg_b.end);
}
return commonSeg.end-commonSeg.start;
}
int findLongestSegment(const vector &segments,int size){
vector lens(size+1);
lens[0]=0;
lens[1]=0;
lens[2]=commonSegment(segments[0],segments[1]);
int tmpLen;
// size>2
// dynamic programming
for(int i=3;i<=size;i++){
lens[i]=lens[i-1];
for(int j=0;j 递归方法:
#include
#include
#include
using namespace std;
typedef struct{
int start;
int end;
}segment;
bool isShorter(const segment &s1,const segment &s2);
segment commonSegment(const segment &seg_a,const segment &seg_b);
int findLongestSegment(const vector &segments,int size,segment &maxSegment);
int main()
{
int n;
int start,end;
while(cin>>n){
vector segments(n);
for(int i=0;i>start && cin>>end){
segments[i].start=start;
segments[i].end=end;
}
}
// sort by segment.end
//sort(segments.begin(),segments.end(),isShorter);
segment maxSeg;
int maxLen;
maxLen=findLongestSegment(segments,n,maxSeg);
cout<<"Longest Length:"<seg_b.end){
commonSeg.start=0;
commonSeg.end=0;
}
else{
commonSeg.start=max(seg_a.start,seg_b.start);
commonSeg.end=min(seg_a.end,seg_b.end);
}
return commonSeg;
}
int findLongestSegment(const vector &segments,int size,segment &maxSegment){
if(size<=1)
return 0;
if(size==2){
maxSegment=commonSegment(segments[0],segments[1]);
return maxSegment.end-maxSegment.start;
}
// size>2
// recursive method
int maxLen,tmpLen;
segment tmpMaxSeg;
maxLen=findLongestSegment(segments,size-1,tmpMaxSeg);
maxSegment=tmpMaxSeg;
// maxSegment=(maxSegment,commonSeg)
segment commonSeg;
for(int i=0;imaxLen){
maxLen=tmpLen;
maxSegment=commonSeg;
}
}
return maxSegment.end-maxSegment.start;
}