判断图的连通性

判断图的连通性

判断图的连通性的方法有3种：并查集，DFS，BFS；

1. 并查集

1. 介绍：
   并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及 查询问题。常常在使用中以森林来表示。
2. 代码展示及说明：

#include
int father[25];
int main()
{
     
	int find(int x);   //查找父节点子函数 
	void Union(int a,int b);//合并两个集合 
	int m,n,V,E,i,k=0;
printf("输入图的边数和点数\n");
	scanf("%d%d",&V,&E);   //输入边和点的个数 
	for(i=1;i<=E;i++){
     
		father[i]=i;    //初始化数组 
	} 
printf("输入所有的边（一行输一条边，即它的两个端点）\n");
	for(i=1;i<=V;i++){
     
		scanf("%d%d",&m,&n);   //输入所有的边，输入边的两个端点 
		Union(m,n);	 
	}
 //图已经搭好了，接下来看它们根节点是否相同，如只有一个相同的根节点，则说明是一个连通图 

	for(i=1;i<=E;i++)    //判断图的连通性 
        if(father[i]==i)k++;
        if(k==1)printf("图是连通的\n");
        else printf("图不是连通的\n");
        return 0;
}
查找根节点的子函数（加上了路径压缩功能）
int find(int x){
                //查找根节点的函数 
    int a;
	a=x;
	while(x!=father[x])x=father[x];
	
	while(a!=father[a]){
         //路径压缩 
		int z=a;
		a=father[a];
		father[z]=x;
	}
	return x;
}
合并两个节点的函数：
void Union(int a,int b){
        //合并的子函数 
	int fx=find(a);
	int fy=find(b);
	if(fx!=fy)father[fx]=fy;
	
}

3. 实例：
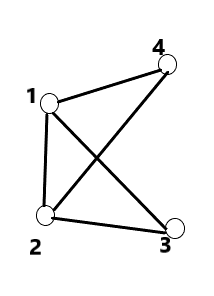
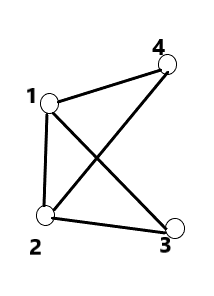
   a) 连通图：
   
   
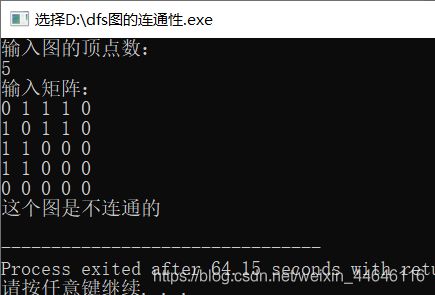
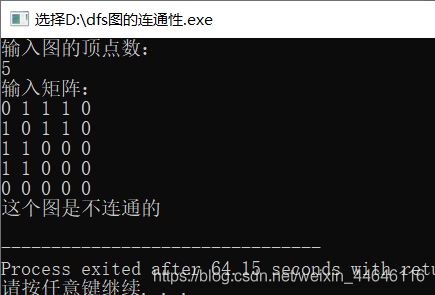
   b) 非连通图：
   
   
   2. DFS
4. 介绍：
   深度优先遍历图的方法是，从图中某顶点v出发：
   （1）访问顶点v；
   （2）依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
   （3）若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。
5. 代码展示及说明：

#include
	int max,n,depth=0;
	#define max 25
	int G[max][max];
	bool vis[max]={
     false};  //用来标记已经访问过的点 ，未访问的为false
主函数： 
int main(){
     
     void dfs(int u,int depth); 
     printf("输入图的顶点数：\n");
	scanf("%d",&n);    //输入顶点数
	int i,j;
	printf("输入矩阵：\n");
	for(i=1;i<=n;i++)    //输入矩阵 
		for(j=1;j<=n;j++){
     
		scanf("%d",&G[i][j]);
	}
	dfs(1,1);//开始从起点遍历 
	int k=0;
	for(i=1;i<=n;i++){
     
		if(vis[i]==false)k=1;
	} 
	if(k)printf("这个图是不连通的\n");
	else printf("这个图是连通的\n");
	return 0;
} 
子函数实现dfs遍历功能：
void dfs(int u,int depth){
        //dfs遍历子函数 
	vis[u] = true;             //访问该点并且做上标记该点为ture  
	for(int v=1;v<=n;v++){
           //找与该点相关的点 
		if(vis[v]==false&&G[u][v]==1)dfs(v,depth++);//找到与该点相连的点，并且该点没有被访问 
	}
}

3. 实例：
   a) 连通图：
   
   
   b) 非连通图：
   

3. BFS

1. 介绍：
   所谓广度，就是一层一层的，向下遍历，层层堵截，还是这幅图，我们如果要是广度优先遍历的话，我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。
   
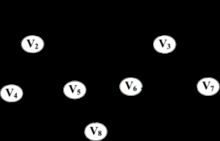
   1、访问顶点vi ；
   2、访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ；
   3、依次从这些邻接点（在步骤②中访问的顶点）出发，访问它们的所有未被访问的邻接点; 依此类推，直到图中所有访问过的顶点的邻接点都被访问；
2. 代码展示及说明：

#include
#include
using namespace std;
 
	int max,n;
	#define max 25
	int G[max][max];
	bool vis[max]={
     false};  //用来标记已经访问过的点 ，未访问的为false 
主函数：
int main(){
     
     void bfs(int u); 
     printf("输入图的顶点数：\n");
	scanf("%d",&n);    //输入顶点数
	int i,j;
	printf("输入矩阵：\n");
	for(i=1;i<=n;i++)    //输入矩阵 
		for(j=1;j<=n;j++){
     
		scanf("%d",&G[i][j]);
	}
	bfs(1);       //bfs遍历开始 
	int k=0;        //做个标记 
	for(i=1;i<=n;i++){
     
		if(vis[i]==false)k=1;   //发现未访问的点，就记k=1; 
	}
	if(k)printf("这个图是不连通的\n");
	else printf("这个图是连通的\n");
	return 0;
	
}
//子函数实现遍历功能：
void bfs(int u){
     
	queue<int> q;  //定义队列q 
	q.push(u);    //将起始点入队 
	vis[u]=true;   //标记起始点为访问过的点 
	while(!q.empty() ){
        //队列非空 
		int u=q.front();  //去队首元素 
		q.pop() ;    //取出队首元素 
		for(int v=1;v<=n;v++){
            
			if(vis[v]==false&&G[u][v]==1){
       //找到与u邻接的未访问点v 
				q.push(v); //将v入队 
				vis[v]=true; //记为访问过的点 
			}
		}
	}
}
   

3. 实例：
   a) 连通图：
   
   
   b) 非连通图：