手把手指导编写数据结构(3.1)——链表拓展(C语言描述)
前言
上一期介绍了最基础的单链表结构,本章介绍补充介绍一些对功能进行增强的链表,也就是双向链表、循环链表以及双向循环链表。因为这些都是单链表的拓展,因此在程序实现上和单链表的很多方法是类似的,我们主要挑代码不同的地方进行详细的解释。
双向链表
简介
单链表只能沿着头结点向后进行遍历,然而如果我们想要倒序查找那么将无能为力。设想这样一种情况,已知末尾结点的位置(这个信息也可以提前存储起来),然后你知道要查询的数据大概在表的后面一段,那么此时如果能从末尾倒序查询将会比顺序查询快不少。
要想实现这样的功能,光是单链表肯定是办不到的,解决办法也很简单,只要在每个结点中再添加一个指向前驱结点的指针(Prev)即可。
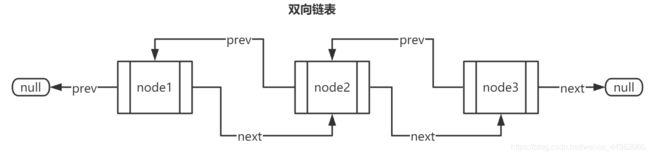
如图上所示,头结点的前驱指针设为NULL,看起来和后继指针是对称的关系呢。
头文件编写
总体来说,单链表具有的函数,双向链表都应该具备,除此之外可以添加几个新的函数。
Position FindForward(ElementType X, Position P, DLinkList L); //从某个位置开始前向查找
Position FindBackward(ElementType X, Position P, DLinkList L); //从某个位置开始后向查找
这两个函数很好理解,输入链表中间一个结点位置之后分别开始向前或者向后进行查找。
C文件编写
结构体
相较于单链表,每个结点多维护一个前驱指针。
struct Node {
ElementType Element;
Position Next;
Position Prev;
};
辅助作用的函数
实际上判断链表是否为空、当前结点是否是最后一个位置等函数与单链表并没有区别,因此这里就不再赘述。
创建和删除表
创建表的过程非常简单,除了单链表的创建操作外,再增加一个Prev指针置为NULL即可。
DLinkList CreateList() {
DLinkList L = (DLinkList)malloc(sizeof(struct Node));
if (L == NULL) {
printf("Out of Space!!!");
exit(1);
}
L->Next = NULL;
L->Prev = NULL;
return L;
}
清空和删除整个链表的操作与单链表无异,不再赘述。
查询操作
常规的查询操作与单链表并没有区别,这里主要来看新添加的两个函数。而对于向后查找来说,相当于将Find函数起始的位置改为了输入的结点位置而已,因此只需将Find函数给P赋值这一行代码改掉即可。而向前查找则只是在每次循环时将结点的后继改为前驱赋值给P即可,与向后查找相比也只在循环内部的一行代码不一样而已。
Position FindForward(ElementType X, Position P, DLinkList L)
{
NullAndExit(L);
PositionInvalid(P);
while (P != L && P->Element != X) {
P = P->Prev;
}
if (P == L) {
printf("Cannot Find the Element!\n");
P = NULL;
}
return P;
}
Position FindBackward(ElementType X, Position P, DLinkList L)
{
NullAndExit(L);
PositionInvalid(P);
while (P != NULL && P->Element != X) {
P = P->Next;
}
if (P == NULL) {
printf("Cannot Find the Element!\n");
}
return P;
}
插入和删除
由于多维护了一个指针信息,因此在插入和删除操作时要稍微复杂一些,我们先来看插入操作,上图。
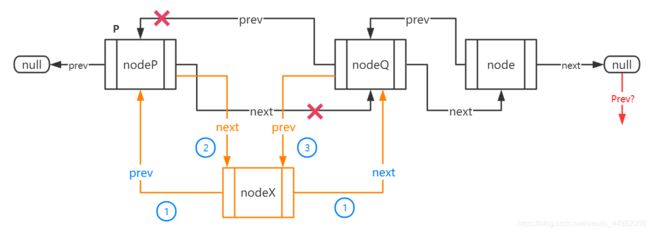
看起来有点眼花,但实际上很简单,只要三步就能搞定了:
- 将要插入的结点的后继指针指向P的下一个结点,前驱指针指向P(因为函数还是定义为将结点插入P位置之后的);
- 将P的后继指针指向新的结点;
- 将P原来的后继结点的前驱指向新的结点,但是如果是在尾部插入呢?表尾没有后继结点,那么也就无需再对其前驱进行修改,甚至执行这样的一步会导致程序出错,因此应该在这个操作前加上一个表尾判断。
void Insert(ElementType X, Position P, DLinkList L) {
NullAndExit(L);
PositionInvalid(P);
Position TmpCell = (Position)malloc(sizeof(struct Node));
if (TmpCell == NULL) {
printf("Out of Space!!!");
exit(1);
}
TmpCell->Element = X;
TmpCell->Next = P->Next;
TmpCell->Prev = P;
P->Next = TmpCell;
if (!IsLast(TmpCell, L)) {
TmpCell->Next->Prev = TmpCell; //注意如果在表尾不加判定会报错
}
printf("Insert Success!\n");
}
在进行第三步的时候,由于我们前面已经将P的后继指向了新结点,所以P(NodeP)已经和其后继(NodeQ)断开了链接。不过好在我们已经将新结点(NodeX)的后继指向了NodeQ,因此直接使用TmpCell->Next来代表Node2即可。
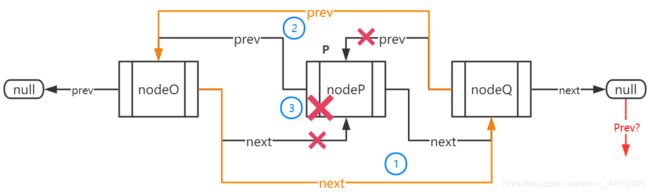
- 将要删除节点P的前驱结点的后继指针指向P的后继结点;
- 将要删除节点P的后继结点的前驱指针指向P的前驱结点,和插入时一样,需要判断是否是表尾,如果是表尾则跳过这一步;
- 删除,释放掉P的内存。
void Delete(ElementType X, DLinkList L) {
NullAndExit(L);
if (IsEmpty(L)) {
printf("The List is Empty!Please Insert First!");
exit(1);
}
Position P = Find(X, L);
NullAndExit(P);
P->Prev->Next = P->Next;
if (!IsLast(P, L)) {
P->Next->Prev = P->Prev; //注意如果在表尾不加判定会报错
}
free(P);
printf("Delete Success!\n");
}
细节讨论
最后,我们深入来讨论一下插入和删除操作的操作。有一个问题是我们之前写的步骤之间顺序是否可以调换?
回答这个问题其实主要就是看调换顺序后跟P位置操作相关的三个结点是否能够保证都被找到。
对于删除操作,无论我们先改前面结点还是后面结点的指针信息,都能够保证可以找到它们,毕竟我们的输入P内部信息并没有变化,其内部就包含了前后结点所在的位置。所以只要最后再释放内存,删除操作的顺序是可以调换的。
这个问题主要主要是针对插入操作的,如果我们将第二步和第三步交换一下可以吗?答案是可以的,而且这样做也许会更好理解,因为NodeQ不仅可以用TmpCell->Next表示,还可以用P->Next来表示(因为此时还没有修改这个指针)。
如果第一步和第三步交换呢?似乎也是可以的,毕竟NodeQ的前驱就是P,即使被修改掉,也有输入的变量存储着P的地址。
但是如果将第一步和第二步交换呢?答案就是不可以了,这也很好理解,因为这样操作后P的后继结点就被修改,原来后面的结点(NodeQ)就找不到了。
你可能会对上面的讨论比较困惑,总而言之,我们只要保证能够找得到需要操作相关的三个结点即可。为了简单起见,我们有一个原则:首先搞定新结点的指针信息,再搞定前后结点的指针信息。这样一来,无论如何写,都能够保证找到结点了。
循环链表
简介
循环链表就是将尾结点的后继指向了头结点的单向链表。因此在结构上与单链表区别不大,结点也没有附加的信息。为什么需要循环链表呢?试想一下,如果我们要让数据进行滚动循环展示,那么此时循环链表就派上用场了。
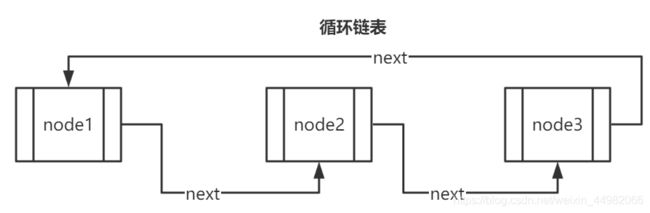
头文件编写
与单向链表没有区别,不再赘述。
C文件编写
辅助作用函数
与单链表不同的是,判断空表和表尾的条件需要修改一下了。单向链表时判断条件是它们的后继是否为NULL,而循环链表则是判断后继是否指向了表头。
int IsLast(Position P, RLinkList L) {
NullAndExit(L);
PositionInvalid(P);
return P->Next == L;
}
int IsEmpty(RLinkList L) {
NullAndExit(L);
return L->Next == L;
}
创建和删除表
创建和删除是和单向链表一致的,但是清空操作需要改动一下。**单向链表的循环条件是P!=NULL,而循环链表应该是P!=L。**其他地方不变。
void MakeEmpty(RLinkList L) {
NullAndExit(L);
Position TmpCell, P;
P = L->Next;
L->Next = L;
while (P != L) {
TmpCell = P->Next;
free(P);
P = TmpCell;
}
printf("MakeEmpty Success!\n");
}
查询操作
同样的,查询操作中的循环条件应该改为P!=L,其他不变。
Position Find(ElementType X, RLinkList L) {
NullAndExit(L);
Position P = L->Next;
while (P != L && P->Element != X) {
P = P->Next;
}
if (P == L) {
printf("No such Element in the List!\n");
P = NULL;
}
return P;
}
Position FindPrevious(ElementType X, RLinkList L) {
NullAndExit(L);
Position P = L->Next;
while (P->Next != L && P->Next->Element != X) {
P = P->Next;
}
if (IsLast(P, L)) {
printf("No such Element in the List!\n");
P = NULL;
}
return P;
}
至于插入和删除操作,和单链表代码是一样的,这里就不再赘述了。
双向循环链表
最后,将上面讲到的两种结构结合起来,就成了双向循环链表。它结合了两个结构各自的优点,结构如图所示。
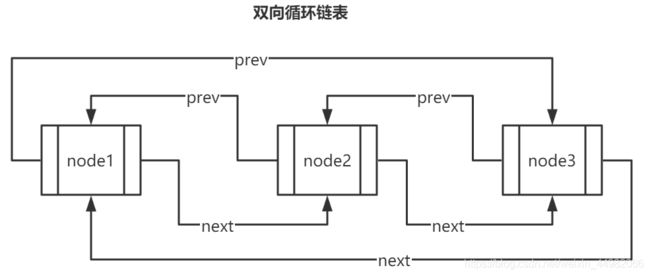
代码编写
实际的代码编写更像是将上面两种结构的代码组合到一起,结点需要维护前驱信息了,插入和删除需要使用双向链表的步骤;而代码中的循环条件和判断操作则需要改为是否为表头了。
我们主要注意插入和删除操作中,由于后继结点不再会出现指向NULL的情况(指向表头了),因此无需在内部添加表尾的判断了。
void Insert(ElementType X, Position P, DRLinkList L) {
NullAndExit(L);
PositionInvalid(P);
Position TmpCell = (Position)malloc(sizeof(struct Node));
if (TmpCell == NULL) {
printf("Out of Space!!!");
exit(1);
}
TmpCell->Element = X;
TmpCell->Next = P->Next;
TmpCell->Prev = P;
P->Next->Prev = TmpCell;
P->Next = TmpCell;
printf("Insert Success!\n");
}
void Delete(ElementType X, DRLinkList L) {
NullAndExit(L);
if (IsEmpty(L)) {
printf("The List is Empty!Please Insert First!");
exit(1);
}
Position P = FindForward(X, L);
NullAndExit(P);
P->Prev->Next = P->Next;
P->Next->Prev = P->Prev;
free(P);
printf("Delete Success!\n");
}
生活中的应用举例
最近经常用三星的gear iconx2018(无线耳机)听歌,我无意中发现其存储的结构和链表有着异曲同工之妙,猜测其内部就是使用的一个双向循环链表对歌曲进行存储的。
这款耳机在不连接手机的情况下,内部也可以储存4G的歌曲文件进行播放(不过只支持mp3),单击一下是播放/暂停,快速双击是切换到下一首歌曲,快速点击三下则是返回上一首歌曲。歌曲只能按照文件存放的顺序进行播放,当播放完最后一首歌后会自动又播放第一首,这不正和双向循环链表的功能是类似的嘛!
看看,我们这么简单就完成了一个耳机当中音乐存储系统的设计,是不是很有成就感呢?: )
总结
至此,线性表的内容基本就介绍完了,在学习完顺序表和链表之后,我们就可以学习一些简单的排序和查找算法了。为了能更好地理解接下来要介绍的跳跃表,下一次将会先介绍一些查找算法,着重介绍二分查找的思想。
最后,我将代码放在了github上:链表拓展C语言版。需要的朋友可以下载。
参考资料
- 《大话数据结构》
- 《数据结构与算法分析(C语言描述)》