【MATLAB】多目标优化算法 NSGA-II (gamultiobj) 的使用

【MATLAB】多目标优化

简单写一写

一个例子

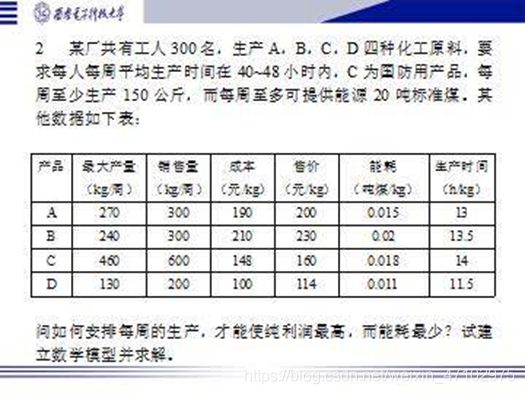
• 建立模型如下

$$\min \text{F}\left(\text{X}\right)=\left(-\text{Z}\left(\text{x}\right),\text{f}\left(\text{x}\right)\right)$$

$$\text{s}.\text{t}.\{\begin{array}{c}\begin{array}{c}{\text{x}}_{\text{i}}⩽{\text{b}}_{\text{i}}\left(\text{i}=1,2,3,4\right)\\ 300\times 40⩽{\sum }_{\text{i}=1}^4{\text{x}}_{\text{i}}{\text{d}}_{\text{i}}⩽300\times 48\\ 150⩽{\text{x}}_3\end{array}\\ {\sum }_{\text{i}=1}^4{\text{a}}_{\text{i}}{\text{x}}_{\text{i}}⩽20\\ {\text{x}}_{\text{i}}⩾0\left(\text{i}=1,2,3,4\right)\end{array}$$

• MATLAB求解如下

clear
clc
fitnessfcn=@Fun;
% 变量个数
nvars=4;
% lb<= X <= ub
lb=[0,0,0,0];
ub=[];
% A*X <= b 
A = [0    0 1 1
    -1/3  0 0 0
     0 -1/2 0 0
     0    0 0 0];

b = [48 ; 30 ; 30 ; 0];

% Aeq*X = beq
Aeq=[1 1 0 0;0 0 0 0; 0 0 0 0; 0 0 0 0];
beq=[120;0;0;0];
%最优个体系数paretoFraction
%种群大小populationsize
%最大进化代数generations
%停止代数stallGenLimit
%适应度函数偏差TolFun
%函数gaplotpareto：绘制Pareto前沿 
options=gaoptimset('paretoFraction',0.3,'populationsize',200,'generations',300,'stallGenLimit',200,'TolFun',1e-10,'PlotFcns',@gaplotpareto);

[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)

plot(-fval(:,1),fval(:,2),'pr')
xlabel('f_1(x)')
ylabel('f_2(x)')
title('Pareto front')
grid on


function y=Fun(x)
y(1)=-(x(1)*100/3 + x(3)*90/3  + x(2)*80/2+x(4)*70/2);
y(2)=x(3)+x(4);
end