opencv Kmeans之图像分割

一、话说kmeans

KMeans算法MacQueen在1967年提出的，是最简单与最常见数据分类方法之一并且最为一种常见数据分析技术在机器学习、数据挖掘、模式识别、图像分析等领域都用应用。如果从分类角度看KMeans属于硬分类即需要人为指定分类数目，而MeanSift分类方法则可以根据收敛条件自动决定分类数目。从学习方法上来说KMeans属于非监督学习方法即整个学习过程中不需要人为干预的学习方法，自动完成整个数据集合分类。对于给定的数据集合DS (Data Set)与输入的分类数目K，KMeans的整个工作原理可以描述如下：

1. 根据输入的分类数目K定义K个分类，每个分类选择一个中心点

2. 对DS中每个数据点做如下操作

• 计算它与K个中心点之间的距离

• 把数据点指定属于K个中心点中距离最近的中心点所属的分类

对K个分类中每个数据点计算平均值得到新的K个中心点

比较新K个中心点之间与第一步中已经存在的K个中心差值

• 当两者之间的差值没有变化或者小于指定阈值，结束分类

• 当两者之间的差值或者条件不满足时候，用新计算的中心点值做为K个分类的新中心点，继续执行2~4步。直到条件满足退出。

从数学的角度来说KMeans就是要找到K个分类而且他们的中心点到各个分类中各个数据的之间差值平方和最小化，而实现这个过程就是要通过上述2~4步不断的迭代执行，直到收敛为止。公式表示如下：

二、关于kmeans算法的一般步骤

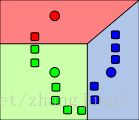
1. k initial "means" (in this case k=3) are randomly generated within the data domain (shown in color).

2. k clusters are created by associating every observation with the nearest mean. The partitions here represent the Voronoi diagramgenerated by the means.

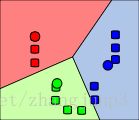
3. The centroid of each of the k clusters becomes the new mean.

4. Steps 2 and 3 are repeated until convergence has been reached.

整个算法的动态算法的动态过程如下图所示：

三、API介绍

double kmeans(InputArray data, int K, InputOutputArray bestLabels, TermCriteria criteria, int attempts, int flags, OutputArray centers=noArray() )

data:  需要自动聚类的数据，一般是一个Mat。浮点型的矩阵，每行为一个样本。

k: 取成几类，比较关键的一个参数。

bestLabels:  返回的类别标记,整型数字。

criteria: 算法结束的标准，获取期望精度的迭代最大次数

attempts:  判断某个样本为某个类的最少聚类次数，比如值为3时，则某个样本聚类3次都为同一个类，则确定下来。

flags:  确定簇心的计算方式。有三个值可选：KMEANS_RANDOM_CENTERS 表示随机初始化簇心。KMEANS_PP_CENTERS 表示用kmeans++算法来初始化簇心（没用过），KMEANS_USE_INITIAL_LABELS 表示第一次聚类时用用户给定的值初始化聚类，后面几次的聚类，则自动确定簇心。

centers: 用来初始化簇心的。与前一个flags参数的选择有关。如果选择KMEANS_RANDOM_CENTERS随机初始化簇心，则这个参数可省略。

四、实验

KMeans在图像处理中经典应用场景就是根据用户输入的分类数目实现图像自动区域分割，本例就是基于OpenCV KMeans函数实现图像的自动分割， 对彩色图像来说，每个像素点都有RGB三个分量，整个图像可以看成是一个3维数据集合，只要把这个三维数据集作为输入参数传给KMeans函数即可，算法执行完毕之后，根据分类标记的索引设置不同的颜色即可。所以演示程序的实现步骤如下：

1. 将输入图像转换为数据集合

2. 使用KMeans算法对数据实现分类

3. 根据每个数据点的分类索引，对图像重新填充颜色，显示分割后图像

int main()
{
	Mat src;
	src = imread("D:\\cv_study\\Exercise\\kmeans\\1.png");
	Vec3b colorTab[] = { Vec3b(0,0,255),Vec3b(0,255,0) ,Vec3b(255,0,0) ,Vec3b(0,255,255) };
	Mat data,label;
	Mat dst = Mat::zeros(src.size(), CV_8UC3);
	int n = 0;
	for(int i=0;i(i, j);
			Mat temp= (Mat_(1, 3) << point[0], point[1], point[2]);
			data.push_back(temp);
		}
	kmeans(data, 3, label, TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 10, 1.0), 3, KMEANS_RANDOM_CENTERS);
	for(int i=0;i(i, j) = colorTab[label.at(n)];
			n++;
		}
	waitKey(0);
    return 0;
}

从上面的结果可以看出，结果不是太理想，但是基本实现了图像的分割。