谈谈黎曼流形与视觉距离错觉问题

转自：https://baijiahao.baidu.com/s?id=1612647738961091671&wfr=spider&for=pc

作者：看海
链接：https://www.zhihu.com/question/30553302/answer/311788410
来源：知乎

data：20190509

一、流形科普知识

1、流形的中文名称

黎曼开始了关于延展性，维数，以及将 延展性数量化的讨论。他给了这些多度延展的量（几何对象）一个名称，德文写作 mannigfaltigkeit, 英文翻译为 manifold，英文字面意思可以理解为 “多层”，中国第一个拓扑学家江泽涵（北大老教授）把这个词翻译为 “流形”，取自文天祥《正气歌》，“天地有正气，杂然赋流形”，而其原始出处为《易经》，“大哉乾元，万物资始，乃统天。云行雨施，品物流形。” 这个翻 译比英文翻译更加符合黎曼的原意，即多样化的形体。。。。。

这是转的，看论文时搜到的，感觉挺解惑的！

这个翻译第一眼看的时候太奇异了！

黎曼，是一个养活了近一个世纪的数学家，并（目测）将要养活接下来至少500年的数学家的男人。

我对数学史不是很熟（以后有机会说不定会开个专栏扒扒历史），所以我这里写的所有和数学史有关的内容你都可以认为我在胡扯（对，我就是懒得查资料……）。今天只想谈谈数学，我会尽量做到科普，所以不要追究我的细节。我对这篇文章的定位是睡前读物，可能很长，但是绝对不会难读懂。

以及，不要因为看了我的文章而走上民科的道路，想要真正了解请老老实实从数学分析线性代数学起。

这篇文章里我只谈两个概念：流形，度量（之一）。

先PS：知乎上总有人问数学到底有啥用，我觉得我可以试试说点用处出来，虽然那些用处肯定不会是那些人的满意答案。

OK，Let's start!

流形的概念绝对是一个非常伟大的构想，以我浅薄的数学史知识，这个概念第一次出现大概就是在黎曼为了谋一份教职而做的一份公开报告里。在黎曼之前，几何几乎就是笛卡尔的坐标（当然这个也是一个非常伟大的概念），大家总是在一个高维的欧氏空间做东西。欧氏空间，大家可以理解为横平竖直的那种空间，比如的三维欧氏空间，就是在牛顿绝对时空观下我们生活的世界。二维的呢？就是高中折磨了大家很久的解析几何。关于这样的空间的例子，其实我们有很好的直观：比如两点之间直线最短，过直线外一点有且仅有一条直线和已知直线平行，三角形内角和180度等等，这些都是大家从小学就知道的事情。黎曼说，你们考虑的东西啊，TOO YOUNG！ TOO SIMPLE！应该考虑所谓的流形。

流形是啥呢？大家知道足球吧，就那个黑白花纹的，一块一块皮缝出来的球形物体。其实每一块皮基本上都是平的（就是你能理解的那种“平”），但是缝起来就是个足球。流形也是一样，它的比较数学化的表述是，有一个点组成的集合M，M中每一个点的附近都有一个邻域，那个邻域和欧式空间“长”的差不多（数学术语叫同胚，很形象的一个词）。还是刚刚的足球，足球上每一个点都在某块皮上，那块皮扯下来就是个平坦的东西。（不要追究细节，不要追究细节！）

这个概念为啥重要呢？因为大家的视野一下子变得不一样了！以前我们看几何对象，我们都是所谓的“外蕴”的看，就是说，我们在这个几何体在的更高维的空间里看它，比如足球，它是个二维的东西（就是一大块布嘛），但是我们是在三维空间看它。所以我们一眼就知道它是弯的！（对，就是你能理解的那个弯）可是假设你是在大航海时代前的人，你怎么知道地球其实是弯的？就跟足球一样弯？你不知道，你就算知道你也不确定你是不是真的知道。对于这种情况最常用的比喻就是，假如你是一只生活在足球上的蚂蚁，你怎么知道你是生活在一个足球上，而不是一个铺了和足球同样材质的、很大很大的（大到你一辈子都走不到边的）桌面上？

流形的概念告诉我们，其实我们真的不知道，因为我们视野范围是有限的，而有限的范围内的东西和横平竖直的欧式空间一模一样……流形的概念伟大之处也在这里，它表明我们其实想要研究更加一般的空间，我们就不应该“外蕴”的去看它，而是应该“内蕴”的去看。什么叫“内蕴”，你就理解为，在流形自身上看。

伟大的黎曼告诉我们，其实“内蕴”的看能知道的东西比你想象的多得多。最简单的，我们是可以在不环游地球不走到太空里的情况下，知道地球是圆的。在说着这个之前，要谈另一个概念：度量。

其实度量从它名字来看就能理解，度量度量，就是量一量长度嘛。人类规定了单位米尺的长度，所以我们就可以度量北京到上海的距离，可以度量你一根手指的长度，一根发丝的长度。对于这种规定了怎么量长度的空间，数学上称为度量空间。而我们最熟悉的那种量长度的方式（其实你只知道这一种，相信我），称为欧氏度量。一个例子就是初中的二维的笛卡尔坐标，两个点之间的距离就是他们横纵坐标的差平方和再开方，那就是二维的欧式度量，也是我们认为最自然的度量。但是（凡事都要有个但是），度量并不是唯一的，就是说还存在其他量距离的方式。

最简单的，我说咱们这么量距离：随便两个不同东西之间的距离都是1（米），相同的东西之间的距离是0（米）（这里最开始有误，给大家造成误导了，现在是正确的版本）。你会发现你想要的性质它都有，比如你会要求 你先去北京再到上海的总路程（我这里是1+1） 不能比 直接去上海的总路程（我这里是1） 短（这个性质称为三角不等式），我这个度量显然满足。你还会要求我从上海到北京的距离和从北京到上海的距离是一样的，你看我的度量也满足，大家都是1。最后，你肯定还要求从北京到北京的距离是0，我的度量依然满足！最后的最后，你会要求说距离不能是负的吧，没事，我这儿要么是1要么是0，都不是负数。（数学上来说，满足这几条性质、再满足距离为零的只能是同一个物体的性质的一个二元函数就是一个度量）

其实咱们老祖宗早就知道了度量不唯一这件事情，所以他们发明了一个成语：缩地成寸。怎么缩地成寸？很简单嘛，定义一个度量（不是我上面说的平凡度量），任何两个东西（比如我和你）之间的距离永远不超过1米（这种度量存在，而且满足三角不等式），那北京到上海多远？反正1米不到。你身高多少？1米不到。你体重多少？……额，那是另外一回事了。注意，我们这里只谈距离（就是你理解的那个距离）

OK，到这里，你脑子里应该有这么一个印象：我们生活的空间的所谓长度，其实只是某一种特定的测量方式得出来的长度，而这种测量方式并不是唯一的。（事实上有无穷多种方式来量，但是它们之中有很多是很无聊的，大家不去研究它们，比如我上面说的那个平凡度量）。下面，最有意思的来了。我们知道地球是个球，它不是欧氏空间，所以不存在无穷延伸的平直的直线，你在地球上随便找个方向一直走，总会回到原点的。所以其实你在地球上用的度量并不是你熟悉的欧氏度量，两点之间直线最短这句话，根本就是骗人！

你的世界观崩溃了有没有！

事实上，欧氏空间也不过是一种特殊的流形，流形才是最本质的概念。黎曼在一般的流形上定义了一类特殊的度量（就是规定了一种特殊的但是会比较有意思的怎么量距离的方式），我们称为黎曼度量。有了黎曼度量，我们就可以研究这个流形到底是不是弯的？有多弯？我们可以研究上面的“直线”是什么东西，从而我们可以研究怎么才能最短的从一个点到另一个点。翻译成人话就是有了黎曼几何，我们确信我们可以知道，一架飞机从北京飞到上海，怎么飞路程最短。甚至，我们在北京做一个足够精确的测量，我们就能知道地球是弯的。

 

鉴于概念已经够多了，这次介绍的先到这儿吧。下次会在这个基础上继续谈谈黎曼几何，重点会介绍到底什么线是最短的，也就是说流形上什么东西是直线的推广。

我说这么多话，其实就是想给大家传达一个意思：数学不难，数学很有趣。但是，想要真正了解数学，请老老实实从数学分析线性代数学起。拒绝民科，从你做起。

 
这篇文章里我只谈两个概念：流形，度量（之二）。

上回说到：我们生活的空间其实是个流形，测量距离的方式叫做一个度量，这回，我们就来聊聊这个流形上的“直线”是个什么玩意儿。

在欧氏空间里你为什么有直线的概念？因为你知道那就是一个坐标轴转一转：你轻轻的拿起x轴，然后在手中挥舞两下，再随便一扔，声称得到了一条直线。众人皆认为你说的好有道理，无言以对。可是流形就麻烦了，它没有坐标轴，它的坐标都是局部的，那直线同学的户口落哪儿好呢？落在北京这个邻域？还是落在上海那个邻域？你可以很聪明的说，很简单嘛，我们在这个邻域甲（就是不想用字母，以防吓坏小朋友）中取一条直线，然后对于和甲相邻的邻域乙（其实数学的定义中会要求这样的两个邻域的交集不是空集，虽然之前的那个足球的例子比较难看出来，你就想象成两块皮要缝起来，总要相互重叠的），我们的甲乙两块皮，哦不，两个邻域相交了，在相交的地方我们的直线已经定义好了（因为在甲上已经定义好了），所以在乙的坐标里面看，你就有一个小线段，我们把它延长，这不就得到了乙中的一条直线么，两个拼起来不就是比原来更长的一条直线了么。这样一步一步，似魔鬼的脚步，延长延长，在这光滑的流形上延长……你想的太简单了，因为你没有办法保证你在甲里面看是直线的东西到了乙里面就一定还是直的！（它会被掰弯的！）

说道这里，就到了我们的主角登场了，那就是真正意义上“直线”同学的身份证：测地线！（此处应有灯光效果+掌声）。

而在正式介绍它之前，我有必要对流形上的度量做一点说明。上次我说，度量就是量距离的方式，而流形往往是一个坑坑洼洼的东西，那上面的线也都是弯弯曲曲的，怎么测量一个弯曲的东西？物理告诉我们，很简单，你开着车走一趟，用每个时刻的速度乘以一小段时间，最后加起来，你就知道多长了。原理就是你在很短时间内把自己走的路当成直线，用你的速度乘以这么一小段时间就得到了一小段直线的距离，把所有这些小线段加起来就能近似原来曲线的长度。当这样的小时间取得足够短的时候，你也就足够接近真实的曲线长度（对学过一点微积分的人而言，这不就是积分嘛）。

速度，在流形上有另外一个高大上的名字叫切向量。一条曲线的长度，就是通过它每一点 切向量大小 的积分得到的。切向量的大小 是虾米？这就是我们的度量真正量出来的。也就是说，我们的度量不是真的测量曲线，而是测量曲线每一点的切向量（就是说我们的度量不是量路程的，它很笨，它只能告诉你速度多大），要得到最终的曲线长度，我们还需要一个积分的步骤。

至此，我们知道了曲线怎么求长度。于是流形上任何两个点之间的一条曲线，我们可以求它的长度，而流形上的“直线”，其实就是这两点间距离最短的那条曲线。既然这么一条曲线是最短的，那我们知道在它周围生活的曲线们都比它长，所以在连接这两个点的所有曲线生活的空间上定义一个函数叫做 求曲线长度函数，那么我们的测地线就是这个 求曲线长度函数 的最小值点。一般来说数学上对于这种最小值，最大值的点，都有办法描述他们，通常是用一些方程来描述。于是，我们的测地线的定义的终极版本粗线了：就是满足某一组特定方程的流形上的曲线。

所以怎么判断一条曲线是不是测地线？很简单，代入那组方程看看是不是成立就好了。反过来，解出那组方程，你就可以知道这个流形上所有的测地线长什么样子。一个很有意思的例子就是，我们亲爱的地球君，它上面的测地线就是所谓的“大圆”，就是所有过球心的平面和地球相交出来的那个圆。终于，我们知道从北京到上海怎么走最短了：取北京，上海，地心三个点，我们知道三个点确定一个平面，这个平面和我们的地表相交于一个大圆，北京和上海都在那个圆上，你只要沿着短的那条弧线从北京跑到上海，数学保证你走的路最短。（当然实际情况更复杂，地球也不是完美的球面）

最后的最后，请和我一起默念三遍咒语：

最短的是测地线，测地线不一定是最短的

最短的是测地线，测地线不一定是最短的

最短的是测地线，测地线不一定是最短的

作者：zero
链接：https://zhuanlan.zhihu.com/p/19880460
来源：知乎

data：20190509
————————————————
版权声明：本文为CSDN博主「起点站」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/HXG2006/article/details/90040990

二、谈谈黎曼流形与视觉距离错觉问题

新智元 AI World 2018 世界人工智能峰会全程回顾新智元于9月20日在北京国家会议中心举办AI WORLD 2018世界人工智能峰会，邀请机器学习教父、CMU教授 Tom Mitchell，迈克思·泰格马克，周志华，陶大程，陈怡然等AI领袖一起关注机器智能与人类命运。爱奇艺上午：https://www.iqiyi.com/v_19rr54cusk.html下午：https://www.iqiyi.com/v_19rr54hels.html新浪：http://video.sina.com.cn/l/p/1724373.html新智元推荐 来源：CAA混合智能专委会作者：张军平，复旦大学计算机科学技术学院教授

【新智元导读】今年中秋节这天，年近九十的数学家迈克尔·阿蒂亚贴出了自己证明黎曼猜想的论文，引发热烈讨论。复旦大学计算机科学技术学院教授张军平的这篇文章内容与黎曼猜想无关，而是想探讨一下黎曼主攻的几何学与人工智能的关系，讨论视觉中的距离错觉问题。

01:37

震撼！AI WORLD 2018世界人工智能峰会开场视频

 

这两天朋友圈在疯传黎曼猜想被破解的消息，2018年9月24日中秋节这天，官科、拿过菲尔兹奖和阿贝尔奖，但已年近90的数学家迈克尔·阿蒂亚贴出了其证明。

 

因为黎曼猜想是一百多年前数学家希尔伯特列出的23个数学最难问题之一，也是现今克雷数学研究所悬赏的世界七大数学难题之一；因为可能揭示素数的分布规律，也因为可能影响现有密码学的研究，大家都很亢奋。不过从众多评论来看，这个尝试可能不得不遗憾地说不是太成功。但考虑到阿蒂亚年事已高，估计没谁敢当面怼他。尽管如此，老先生老骥伏枥、志在千里的钻研精神还是值得我辈学习的。

 

作为始作俑者，黎曼可能压根也没想到自己的猜想能对100多年后的密码学有所帮助。因为研究素数在“科学的皇后”——数学里被认为是最纯的数学，是与应用毫无关系的数学。这种纯性让数论成为了“数学的皇后”。所以，正常情况下，数学的鄙视链是不允许他去推测素数分布在密码学中的应用的。

 

据说，站在数学鄙视链顶端的纯数学研究者，通常是看不起学应用数学的；而学应用数学的，会看不起学统计的。在人工智能热潮下，学统计的又看不起研究机器学习的；而学机器学习的会看不起做多媒体的；而做多媒体的又看不起做数据库的。纯做密码学研究的，鄙视链应该在应用数学与机器学习方向之间，哪会被才高八斗的黎曼看上？

能看上黎曼的自然也是大牛， 当年是德国数学家高斯看中了他并理解了他的几何学观点。今天要讲的也不是黎曼猜想，而是黎曼的几何学观点与人工智能的关系。

 

当年，黎曼申请来到哥廷根大学做无薪讲师，就是学校不提供固定薪水、讲了课才有薪水的教师。初来乍到，来场学术报告是必需的。当时的学术委员会从黎曼推荐的三个选题中选了一个他最意外的题目，要他以“关于几何学的基本假设”为主题来做就职报告 。

 

那个时候，公元前三世纪希腊亚历山大里亚学派的创始者欧几里德编写的数学巨著《几何原本》中的五条公设中，连大猩猩都很痛恨的第五公设，就是“平行线没有香蕉(相交)”的第五公设，已经被罗伯切夫斯基于1830年证明不成立。他认为在一个平面上，过已知直线外一点至少有两条直线与该直线不相交。由此开创了非欧几里得几何，虽然他的理论在其死后12年才逐渐被认可。

 

而黎曼开创的非欧几何则断言，在平面上，任何两条直线都必然相交 。他们的发现，最终奠定了非欧几何的数学基础。直观来说，就是以前以为是可以用直线测量准确距离的世界，现在居然要弯了。

 

既然弯了，那就很容易找到相交的可能。比如从篮球的顶部到底部，让蚂蚁沿着表面爬，它只能爬出曲线，且总是相交的。在这个篮球曲面上测得的“直线”距离就只能是弯的，称为测地线(Geodesic)。

 

在黎曼用了七周时间准备的报告中，他希望在能用直线测距离的欧氏空间和非欧空间之间找到合理的衔接。于是，他假定非欧空间可以由好几个局部欧氏空间拼接而成的，提出了多个(英文的前缀是mani) 折或层(英文的词根是fold)的概念，即流形(manifold，对应的德语是mannigfaltigkeit)。

 

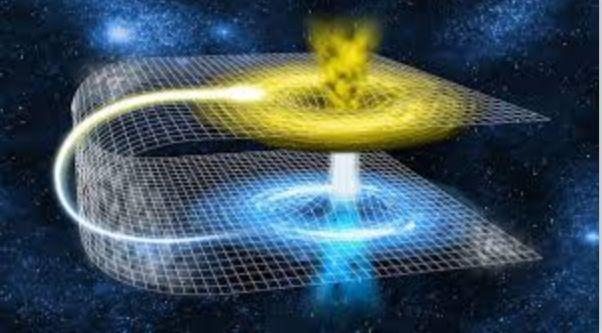
简单且不严格来说，就是流形可以用一块块的小粘土以任意形式粘在一起来表征，但每块局部的粘土又跟我们常见的欧氏空间是一致的，如图1所示。至于相邻粘土块之间的联接关系，则要把连续性、光滑性、可微性、抽象性等众多深奥概念考虑进来，这样便成了多数人只能看懂目录的微分流形。

图1 局部欧氏与黎曼流形：二维流形或曲面M上的一个局部p (橙色区域)与欧氏空间中的黄色区域等价。

 

后来，爱因斯坦知道后，如获至宝。便找了当年他提出狭义相对论时，用到过的洛仑兹变换的数学家洛伦兹本人，请他帮助学习微分流形基础。在他的帮助下，最终爱因斯坦基于加速度下的不变性原理提出了广义相对论，将牛顿提出的万有引力归结为是弯曲空间的外在表现，开启了宇观物理学。

 

不过，那个时候，计算机还没诞生，也没人会意识到黎曼提出的流形与人工智能有什么关系。

感知的流形方式

 

回到人的智力发育上讨论这一关系的存在性。儿童在发育过程中，空间感是逐渐形成的。在他学习观察世界的过程中，一个需要扫除的认知障碍是遮挡。有心理学家做过实验，在小孩面前放一个屏障，然后将小孩面前的玩具移到屏障后。小孩会感觉很吃惊，但却不会绕到屏障后去寻找玩具。这说明在发育的初始阶段，小孩缺乏对三维空间尤其是空间深度的理解。经过一段时间后，他的这种障碍会消除 ，对物体空间能力的辩识也明显加强。

 

 

图2 旋转不变性

 

于是，儿童启蒙课本中便会出现这样一个新的测试题。放一个奇形怪状的积木，然后给几个不同旋转角度的形状，其中一个或多个是该积木旋转后的真实图像，也有不是的，让小朋友自己去判断和识别哪些是原来的积木旋转过来的。令人惊奇地是，小朋友慢慢都会学会如何处理这种旋转，并能准确判断。这种旋转不变性能力的获得，在格式塔心理学中有过相应的观察和描述。该现象似乎在告诉我们，人的大脑能对每一个见到的物品进行自动的旋转。

 

那么，人是如何记忆这些见过的物品，并实现自动旋转的呢？格式塔心理学中没有给出终极答案。

 

而认知心理学则对记忆给了一种可能解释，叫原型说(prototype)，即某个概念都会以原型的形式存储在记忆中，神经心理学进一步给了假设性的支持，称记忆是存储在离散吸引子(discrete attractor)上。尽管这一解释维持了相当长的时间，但并没有就为什么大脑可以实现自动旋转给出圆满答案。

 

2000年的时候，普林斯顿大学教授Sebastian Seung 和宾州大学教授Daniel Lee 在《Science》上发了篇论文。他们认为人是以流形方式来记忆的。以视觉感知为例，假定人的视网膜只有三个视神经元，不考虑颜色的变化， 每个神经元能感受一定的光强变化，那么看到一个母亲的人脸后，视神经元上会有三个响应。

 

如果三个视神经元是相互独立无关的，那就可以把每一个视神经元看成一个维度，就会有一个由三个维度张成的欧氏空间。如果把只是做了侧向角度变化的、母亲的照片读入这个的空间， 那三张图3所示的图像在此空间会有何规律呢？

 

理论上讲，如果只做了侧向角度变化，那这个变化就是三张图像的内在控制量。只有一个变量，但又不见得会是直线，所以，母亲的照片按角度的顺序连起来，就会是一条曲线。类似的，如果把小朋友侧向角度变化的照片也输进来，那同样在这个三维空间会是一条曲线。但可能与母亲的不在同一条曲线上。如果这个假设成立，那么记忆就可能是沿着这两条不同的曲线来分别还原和生成不同角度的母亲和小孩图像。也就能部分解释，为什么人只用看陌生人一两眼，就能认出其在不同角度时的面容。

 

 

图3 母亲和小孩的流形感知方式，假定眼睛只有三个视神经元，母亲小孩均只有一个自由度，即左右转头。[1]

 

如果再进一步，假设母亲小孩有两个自由度的变化 ，如左右、上下角度的变化，那这两个维度的变化在三维空间上可以张成无数条曲线的合集，即曲面。在流形的术语中，曲线可以称为一维流形，而曲面则为二维流形。

 

如果假定变化再丰富点，比如角度的变化有上下角度、左右角度；还有表情的变化，真实和细微的微表情，光照的变化，年龄的变化等诸如此类的，我们把这些变化的维度称为人脸变化的内在维度，是真正需要记忆的。

 

相比较于人眼里上亿的视神经元总数来说，这些内在维度可以张成的空间比上亿维神经元张成的空间要小非常非常多。我们便可以在曲面的名字上再加个超字来刻画，叫超曲面，也称为低维流形。考虑到输入进来的信息是通过神经元的，所以，又能名字叫得更学术点，称其为嵌套在高维空间(视神经元空间)的低维流形。

 

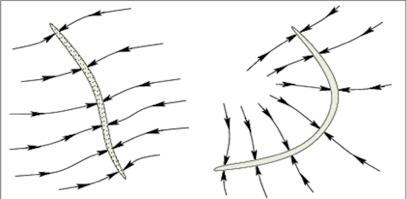
与经典的原型学说的主要不同在于，假设用于记忆的离散吸引子能被替换成了连续吸引子，于是存储在大脑里的原型便不再是一个点，而可能是一条曲线、一个曲面甚至超曲面。视觉看到的任何内容，都会从不同途径收敛到这个连续吸引子上，并在此吸引子上实现对不同角度和不同内在维度的外推。这在某种意义上既解释记忆的方式，又解释了自动旋转问题。因此，黎曼流形的构造有可能解决格式塔心理学中提及的“旋转不变性”问题。

 

图4 左：离散吸引子；右：连续吸引子[1]

 

那能否让计算机也实现类似的自我旋转或推理能力呢？如果能实现，也许就往人工智能方向迈进了一小步。

关于流形学习的研究

 

以人脸为例，先看下最初的人脸识别技术。早期的做法是遵循欧氏空间距离，按最短直线距离来评判。这样做的不足是没有处理好不同角度、不同光照的人脸识别。试想想，如图5所示的不同角度的A，以及相同正脸的B，假如识别是基于相同像素位置的光强差异平方总和的最小值来实现，那哪两张会更近呢？显然相同角度的A和B距离会更近。这就是欧氏距离直接用于人脸识别的不足。

 

图5 不同角度的两个人的照片

 

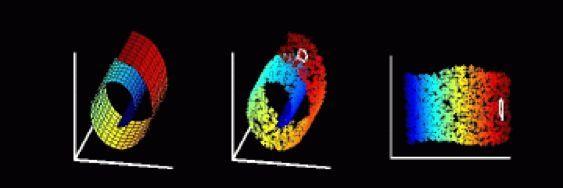
为什么计算机没有人脑的旋转不变性呢？图6显示了一组人脸在摄像机前仅进行平移而保持其它性质不变的图像集。如果把每个像素视为一个维度，则每张照片可视为高维空间的点，则多次采集的多个人的照片集合看成是该空间的点云。通过某些简单的统计策略总结出前三个主要的维数，再将点云投影到这个三维空间并两两描绘出来，便有了图6的曲线图。

 

 

 

图6 人脸内在维度示例[2]

 

不难发现，只控制了角度旋转的图像序列变成了一条又一条的曲线，这正是我们上面讨论的曲线，一维流形。 实际上，如果限定采集时的变量为人脸到摄像机前的远近变化，结果也是一样。这一实验部分印证了人脸图像的内在控制变量是低的。因此，如果希望计算机能对不同角度的人脸有合理的推测功能，和还原格式塔心理学中的旋转不变性时，找到流形结构并依照它的规则来办事就很自然了。

 

图7 各种复杂的流形结构：瑞士卷(Swissroll)； 右： 双螺旋线

 

但是，数据形成的流形结构并非只有曲线一种情况，它可能会有如图7所示的瑞士卷的复杂结构。他可能还不止一个，比如两个卷在一起的双螺旋线。那么，要想利用经典又好使的欧氏距离来解决问题，可行的方案之一就是把它们摊平或拉平，这样，我们待分析的数据所处的空间就是欧氏空间了。于是，有大量的流形学习的工作便在此基础上展开了。

 

最经典的两篇是与《流形的感知方式》几乎同时于2000年发表在Science上。因为计算机科学的工作很少有发Science的，能发在上面，则有可能引导大方向的研究。所以，这三项工作被视为引领了2000年后流形学习发展的奠基之作。

 

其想法现在来看的话，其实并不复杂。首先两篇文章都引入了邻域 的概念，也就是局部情况下，流形等同于欧氏空间，因此，短程距离用欧氏度量来计算是合理的。

 

不同的是，Tenenbaum的工作是从测地线距离的计算来考虑的。

 

试想如果有一张纸，纸上有三个点，A、B和C，AB比AC在纸面上更近。但如果把纸弯成图8的形状，再按直线距离来算时，AC就会更近。但按流形的定义，AC这条路径是不能出现的，因为这个纸就是一个空间，是一个不能为二维蚂蚁逃脱的空间。因此，更合理的计算方式是把图8右图的红色曲线长度，即测地线精确算出来。

 

 

图8 测地线距离和局部等度规(Isomap)算法 [3]

 

但测地线是在连续意义定义的，要根据离散的数据点来算的话，Tenenbaum等找了个平衡，提出了基于图距离的局部等度规算法。他们假定邻域内的点与点之间相连的距离都等于1，邻域以外的距离都强设为0。因为流形可以由若干个小的邻域来粘合构成，而相邻的邻域总会有部分的重叠，那么，如果把所有距离为1的都连条边出来，则原来的数据点就构成了一张连通图。而远点的距离或者所谓的测地线距离，就可以通过连通的边的最短距离来近似了，如图8中图所示。于是，就可以为所有的点建立一个相似性或距离矩阵。有了这个矩阵，再通过统计方法就能找到其主要的几个方向了，即摊平的低维子空间，如图8右图所示，蓝色的测地线距离就为红色的图距离近似了。

 

而Roweis和Laul当时则从另一角度来尝试恢复这个平坦的空间。他假定邻域内的数据点会相互保持一种几何关系，关系的紧密程度由权重来决定，权重的总和等于1。同时，他假定这个权重诱导的关系在平坦空间会与观测的空间保持一致，即局部结构不变。当然，还得防止数据在还原到低维的平坦空间时不致于坍缩至一点去。基于这些假设，很自然地就把优化方程写了出来，并获得了不用迭代求解的闭式解，即局部线性嵌入算法，如图9所示。

 

算法比较直白，但两篇文章都发现了类似于图3和图4的现象，即约简到二维平面后，数据的分布具有物理意义的。比如，手旋转杯的动作会沿水平方向连续变化 ，人脸图像的姿态和表情会在两个垂直的轴上分别连续变化 。而这种情况，以前的算法似乎是找不到的。除此以外，这两篇工作的成果又很好地与“感知的流形方式”吻合了。

 

 

图9 局部线性嵌入(LLE)算法[4]

 

还有一点，邻域的大小决定了流形的表现。按几何学大牛Spivak的说法，邻域如果和整个欧氏空间一样大的，那欧氏空间本身就是流形[5]。所以，流形学习的研究并非是一个很特别、很小众的方向，它是对常规欧氏空间下研究问题的一般性推广。

 

于是，从2000年开始，国内外对流形学习的研究进入了高潮，希望能找到更有效的发现低维平坦空间的方法。比如希望保持在投影到平坦空间后三点之间角度不变的保角算法；比如希望保持二阶光滑性不变的海森方法；比如希望保持长宽比不变的最大方差展开方法；比如希望保持局部权重比不变的拉普拉斯算法等。不过何种方法，都在尝试还原或保持流形的某一种性质。也有考虑数据本身有噪导致结构易被误导的，比如我们经常在星际旅行中提到的虫洞现象，如图10。它可以将原本隔得很远的两个位置瞬间拉近。在数据分析中，称虫洞为捷近或短路边(shortcut)，是需要避免的，不然会导致还原的空间是不正常甚至错误的。

 

 

图10 将图8中的A和C连接的虫洞或短路边(Shortcut)问题

 

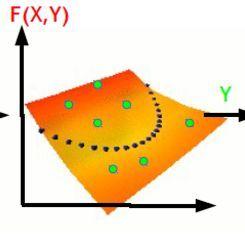
除了找空间外，流形的一些性质也被自然地作为约束条件加入到各种人工智能或机器学习的优化算法里。即使是现在盛行深度学习研究中，流形的概念也被很时髦地引了进来。如生成对抗网在2014年最初提出的时候，Yann LeCun就指出希望对抗的数据处在数据流形中能量相对高的位置，而真实数据则位于流形能量相对低的位置，这样，就有可能让生成对抗网获得更好的判别能力。

 

 

图11 生成对抗网中的流形; 左: 高能量值；右：低能量值 [6]

关于流形学习的思考

 

虽然流形学习在认知、机器学习方面都有很好的可解释性，不过这几年随着深度学习的盛行，与它相关的文献在相对份量上正慢慢减少。一个原因是，由于这一波人工智能的热潮主要是产业界开始的，而产业界对预测的重视程度远高于可解释性。所以，不管学术界还是产业界都把重心放到如何通过优化深度学习模型的结构和参数优化去了。

 

正如我之前强调过的，过分关心预测性能的同时，必然会牺牲可解释性。因为前者关心个例，后者需要统计。两者是一个矛盾，类似于测不准定理中的速度和位置的关系。从目前的情况来看，牺牲的可能还不止流形学习这一种具有可解释性的方法。尽管大家在讨论数据的时候，还会时不时说下流形，但最多也只是扔个概念出来，并没有太多实质性的融入。

再回到人的大脑来看，虽然之前也提到了流形的感知方式，但是否存在实证还不是完全的明确，Seung和Lee也只是做了些间接的推测。一方面，是测量技术的不足，因为现在都是采用脑电图描记器(EEG)或磁共振成像(MRI)技术来检测大脑信号的，本身就缺乏这种连续性的关联，要寻找是否大脑中存在流形记忆确实有难度。

 

另一方面，我们的大脑里面真有一个弯曲的流形记忆空间呢？真是以连续而非离散吸引子形式存在吗？如果是的，那与现在深度学习的预测模型的做法应该是不同的，其差别就如同飞机和鸟。

 

也许，找寻这个问题的答案，和黎曼猜想的破解是一样的困难。

 

本文作者

 

 

张军平 ，复旦大学计算机科学技术学院教授、博士生导师，中国自动化学会混合智能专委会副主任。主要研究方向包括人工智能、机器学习、图像处理、生物认证及智能交通。至今发表论文近100篇，其中IEEE Transactions系列18篇，包括IEEE TPAMI, TNNLS, ToC, TITS, TAC等。学术谷歌引用2700余次，ESI高被引一篇，H指数为27。

 

参考文献：

1. H. Sebastian Seung, Daniel D. Lee. The Manifold Way of Perception. Science 290 (5500): 2268-2269.

2. 李子青，张军平. 人脸识别的子空间统计学习. 机器学习及应用，清华大学出版社，2006，pp.270-301.

3. J. B. Tenenbaum, V. de Silva, J. C. Langford. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 290 (5500): 2319-2323

4. S. Roweis, L. Saul. Nonlinear dimensionality reduction by locally linear embedding. Science 290 (5500): 2323--2326.

5. Michael Spivak. A Comprehensive Introduction to Differential Geometry, Vol. 1, 3rd Edition. Publish or Perish, 1999.

6. LeCun Yann. Predictive Learning. Slide at NIPS 2016.

 

 

更多阅读

马斯克：人类极有可能生活在更高文明模拟的矩阵游戏中

强化学习重大突破：DeepMind用一个AI在57个游戏中全面超越人类

新智元AI WORLD 2018

世界人工智能峰会全程回顾

 

新智元于9月20日在北京国家会议中心举办AI WORLD 2018世界人工智能峰会，邀请机器学习教父、CMU教授 Tom Mitchell，迈克思·泰格马克，周志华，陶大程，陈怡然等AI领袖一起关注机器智能与人类命运。

 

全程回顾新智元 AI World 2018 世界人工智能峰会盛况：

爱奇艺

上午：https://www.iqiyi.com/v_19rr54cusk.html

下午：https://www.iqiyi.com/v_19rr54hels.html

新浪：http://video.sina.com.cn/l/p/1724373.html