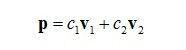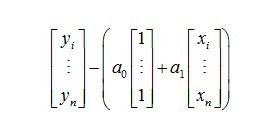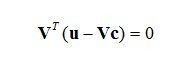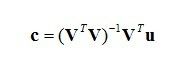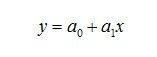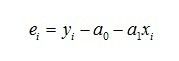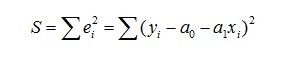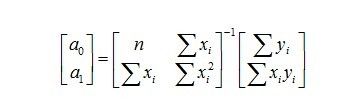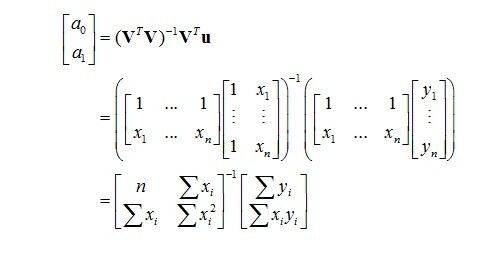最小二乘法 几何意义
上次写了篇文章来阐述几何投影与傅里叶级数的联系,今天我想谈谈几何投影与最小二乘法的联系,这种联系的好处是不管多复杂的公式,又可以被瞬间记住了。本文的中心思想是:最小二乘法中的几何意义是高维空间中的一个向量在低维子空间的投影。这个思想在MIT教授Gilbert Strang的线性代数的公开课程上有讨论,这里我会把这个思想详细的阐述一遍。文章最后会把傅里叶级数和最小二乘法放在一起做个比较和总结,希望大家能体会到两个看起来风马牛不相及的概念其实是如此相似。
1. 三维空间的向量在二维平面的投影
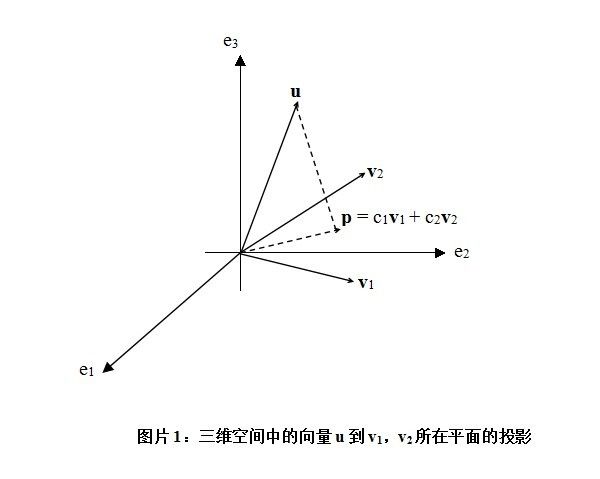
首先我们需要先复习一下三维空间的向量在二维平面的投影。这是高维空间的向量到低维子空间投影的最简单的例子,理解了三维到二维的投影,更高维的情况大家是很容易扩展的,因为二维子空间(即二维平面)和更高维子空间都可以由矩阵来表示。这里我不用二维到一维的投影做例子是因为这个时候低维子空间只是由一个向量表示,并不具备矩阵的一般性。
如图片1所示,在三维空间中给定一个向量 u,以及由向量 v1,v2 构成的一个二维平面,向量 p 为 u 到这个平面的投影,它是 v1,v2 的线性组合:
我们要回答的问题是:如何求出 c1,c2 的表达式?相信看过我上篇日志的朋友都知道怎么求了,只要利用 u - P 这个向量分别与 v1,v2 垂直这两个条件,就能求出 c1,c2。用数学语言来表示,就是下面这两个式子。 ![]() (2)
(2)
为了方便之后扩展到更高维的情况,我们把它们合并成一个式子,令 V = [v1,v2],则 (2) 式等价于
把 (1) 式带入 (3) 式,然后矩阵转置(transpose)一下(这么做只是为了方便求解),得到以下这个式子
这里的 c = [c1,c2]T。所以系数 c 的表达式为
注意这个表达式明显适用于更高维的情况。如果我们用二维到一维的投影来举例,那么上式中的 VTV (这里的T是矩阵转置,本来在word里是上标的,传到人人格式就变了)将会出现在分母当中,就像上篇日志的 (3) 式那样,这个形式就太有局限性了。另外值得注意的是我们考虑的 v1,v2 不是正交的,所以 c1,c2 不能由 u 到 v1,v2 分别投影来求。
2. 最小二乘法
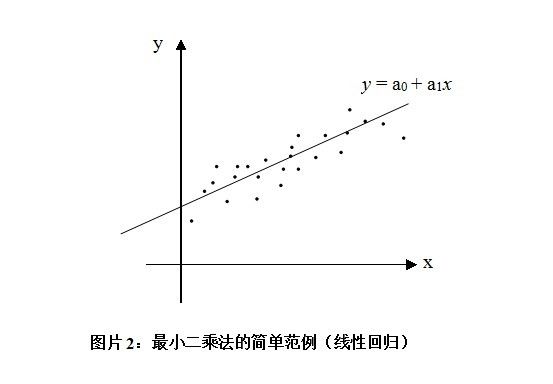
我们来回顾一下什么是最小二乘法。假设我们手上有n组成对的数据,{(xi,yi): i = 1, 2, ... , n},为了探究 y 变量和 x 变量的关系,我们希望用一个多项式来匹配它,可是多项式中的系数怎么确定呢?拿来拼凑肯定是不行的,最小二乘法告诉我们,这个多项式的系数应该让每个点的“误差”的平方之和最小。举个简单的例子,如下图所示,我可以用一个线性函数来匹配这些数据(也叫做线性回归),也就是
那么每个点的误差可以写成
我们想要最小化误差的平方和,也就是下面这个关于 a0,a1 的函数(注意,xi,yi都是已知的数据):
这是个函数求极值的问题,我们很快想到可以用微积分中的求导为零来列出两个方程,从而求得 a0,a1。这里我就不罗列整个过程了,只给出最后的答案,大家有兴趣可以自己演算一下。答案可以写成下面这个矩阵形式。
可以想象,如果是2次,3次, 甚至更高次多项式,系数的推导会变得更复杂。接下来我要做的事就是用几何投影的角度来看最小二乘法,而且不管多少次的多项式,系数的表达式都可以马上写出。
还是以上面这个线性函数为例,我们现在重新审视 (8) 式。各项的平方相加这件事情,其实我们不是陌生的,还记得怎么算向量的长度么?不就是各项平方相加,再开根号么?你现在应该看出来 (8) 式究竟是什么东西了,它就是下面这个向量的长度平方:
看不出来的同学再仔细看看 (10),它的长度平方就是 (8) 式!把误差的平方和看成这个向量的长度平方这件事情有什么好处呢?请容许我慢慢解释。首先我们知道要让这个向量长度平方最小,等同于让它的长度最小。我们仔细看下 (10) 这个向量的长度究竟代表了什么意思,先看小括号里是什么东西,它是两个向量 [1, ... , 1]T 和 [x1, ... , xn]T 的线性组合,换句话说,它是这两个向量构成的二维子空间(想成一个平面就可以)的任意一点。所以 (10) 这个向量的长度表示向量 [y1, ... , yn]T 到这个二维子空间任意一点的距离!把 (10)这个向量长度最小化的意思是:寻找在 [1, ... , 1]T 和 [x1, ... , xn]T 构成的二维子空间上的一个点,使得向量 [y1, ... , yn]T 到这个点的距离最小。怎么找这个点呢?根据第一部分的铺垫,相信你已经有答案了,只要做一个几何投影就好了。
我们只要把图片1中的 u 替换成 [y1, ... , yn]T ,把 v1,v2 分别替换成 [1, ... , 1]T 和 [x1, ... , xn]T, 系数 c1 和 c2 也就是我们要求的 a0,a1,可以马上由 (5) 式得出
这和之前求得的 (9) 式是完全一样的!令人感到惊喜的是,全程我们都没有用到微积分,我们需要的知识只是简单的几何投影!
如果你看懂了全过程,相信你也可以轻易的把这个方法应用到更高阶的多项式,我们只要在 (11) 式中相应的更改子空间就好了,推导是瞬间完成的。当然我假设你能用电脑来计算矩阵求逆。
最后我总结一下,最小二乘法的几何意义是高维空间的一个向量(由y数据决定)在低维子空间(由x数据以及多项式的次数决定)的投影。我们不妨回顾一下傅里叶级数的几何意义是:无穷维空间的一个函数在同一空间中按照一组正交基(也就是一系列新的坐标轴)展开,这里的展开可以看成是函数先在同一空间投影到其自身,然后这个函数在各个新坐标轴上分别投影决定了展开系数(也就是新坐标)。最小二乘法和傅里叶级数,两个看起来完全不同的概念,从几何的角度来看是极其相似的,前者是高维到低维的投影,后者是无穷维到无穷维的投影;它们的区别是,前者在投影的过程中维度变少了,这可以理解为信息变少了,因为我们用了简单的多项式来匹配一堆可能蕴含复杂关系的数据,后者是同一空间中的投影,只是换个坐标体系而已,维度不变,这可以理解为信息不增也不减,因为一个函数的傅里叶级数只是它的另一个表达方式,两者包含的信息完全是等价的。
我在写完这篇文章后的感悟是,数学中总是存在着许多看似不同,其实却很相似的概念。比如最小二乘法和傅里叶级数都可以看成是几何投影,对函数求导和对向量乘以矩阵都可以看成是线性变换,一个数有正负号而一个矩阵也有其正定性,矩阵和常微分方程都有特征值问题,一次线性常微分方程和一次线性常微分方程组的求解都可以用积分因子的方法(不知道大家知不知道这个,我第一次发现的时候感觉非常惊喜),线性时不变系统的反应和概率中多个独立随机变量之和都能写成卷积的形式,扩散方程中的极大原理(maximum principle)和复变函数中的最大模原(maximum modulus principle)有着极其相似的描述,光学和力学中也都有最小作用量原理,统计力学和信息论中的熵(entropy)这个概念都是不确定性的一种度量,信号处理和量子力学中存在着看起来截然不同但是本质却相同的不确定性原理。人们有时也会人为的创造相似的概念,从大自然当中去寻找灵感,比如算法中的遗传算法借鉴了达尔文进化论的思想,模拟退化算法借鉴了金属冷却的概念,机器学习借鉴了人类的学习过程,控制论由维纳最初提出,他把动物有目的的行为赋予机器从而促使了一门新学科的诞生。所有这些相似性,都能让学习的过程增添许多趣味,也使我们更好的去理解这个世界。在以后的日志中我会陆续对上面提到的这些相似概念做一些专题讨论,希望大家继续关注。