0x00 随机
我们不能预测天空中乌云的样子,因为它的纹理总是具有不可预测性。这种不可预测性叫做随机 (random)。
在计算机图形学中,我们通常使用随机来模拟自然界中的噪声。如何获得一个随机值呢,让我们从下面的函数入手:
y = fract(sin(x) * 10000.0);
这里,sin(x) 乘以了一个很大的数:10000.0,使得 x 值的一点微小变化也会引起计算结果的剧烈变动。同时,根据 sin 的图形我们可以知道,在一个小范围内,sin 函数的变化率总是不同的。结合这两点,再使用 fract() 函数提取整个表达式的小数部分,这样就能得到的一系列呈现出随机状态的值。
我们可以用这个函数来生成随机值。但是,这里的随机是伪随机的,因为对于相同的 x 计算的结果都相同。
0x01 噪声
上面函数得到的随机值是在一个维度变化的。为了将其应用到二维中,还需要将二维的坐标值转化为一维的浮点数。这一步可以使用点乘来实现。
y = fract(sin(dot(st, vec2(12.9898, 78.233))) * 43758.5453);
你可能注意到上面的表达式中有三个很奇怪的数字。有什么特殊含义吗?没有!这三个数字是我从其他地方复制粘贴来的。事实上,这三个数并不是固定的。也可以对其进行修改,从而得到不同的随机效果。
将 uv 坐标代入上面的表达式中,并将返回的结果赋值给该坐标点的颜色,就能得到一张噪声图了。这样生成的噪声并不具备连续性,点与点之间的值存在着很大的差异。
这样的噪声被称作白噪声,完整代码如下:
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
float random(vec2 pos) {
return fract(sin(dot(pos.xy, vec2(12.9898,78.233)))* 43758.5453123);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
float f = random(st);
gl_FragColor = vec4(vec3(f), 1.0);
}
0x02 平滑
和白噪声相比,自然界中的噪声并非如此杂乱无序。比如本文开头的乌云,就没有白噪声这样的颗粒感。因此,我们需要进一步加工,让噪声图变得更平滑,点与点之间的过渡更自然。
一种通常的做法是,对于任何一个点,都求它所在的单位格子的四个顶点的值。再使用平滑插值函数:\(f(x) = 6x^5 - 15x^4 + 10x^3\) 对这四个点的值进行插值,将插值的结果赋给原先的这个点。
对于原本归一化的 uv 坐标来说,这样会得到一幅完全平滑过渡的图,少了一些随机性。所以在代码中,还需要将 uv 的范围扩大,这样就能得到更多变化。
这样的噪声被称作 Value Noise,具体代码如下:
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
float random(vec2 pos) {
return fract(sin(dot(pos.xy, vec2(12.9898,78.233)))* 43758.5453123);
}
vec2 smooth(vec2 t) {
return t * t * t * (t * (6.0 * t - 15.0) + 10.0);
}
float noise(in vec2 st) {
// vec2 i = floor(st);
vec2 s = smooth(fract(st));
// float bl = random(i);
// float br = random(i + vec2(1.0, 0.0));
// float tl = random(i + vec2(0.0, 1.0));
// float tr = random(i + vec2(1.0, 1.0));
float tl = random(vec2(floor(st.x), ceil(st.y)));
float tr = random(vec2(ceil(st.x), ceil(st.y)));
float bl = random(vec2(floor(st.x), floor(st.y)));
float br = random(vec2(ceil(st.x), floor(st.y)));
float t = mix(tl, tr, s.x);
float b = mix(bl, br, s.x);
return mix(b, t, s.y);
}
void main() {
vec2 st = gl_FragCoord.xy / u_resolution.xy;
st *= 10.0;
// st *= 100.0;
float n = noise(st);
gl_FragColor = vec4(vec3(n), 1.0);
}
上面代码中注释的部分来自 The Book of Shader 给出的例子,该例子对于格子的边界如 y = 3.0 处,将会取到 floor(3.0) + 1.0 = 4.0 的值,如果两个点的噪声值差距较大,则会造成格子间出现明显的分割线。因此,改用 ceil 来计算原点所处格子右边和上边的边界值,可以保证其位于格子中。
另外,不妨试着将 st 乘上更大的系数,比如再乘上 100。可以发现,当 st 来到一个更大值的时候,噪声图又会重新变成白噪声。
0x03 柏林
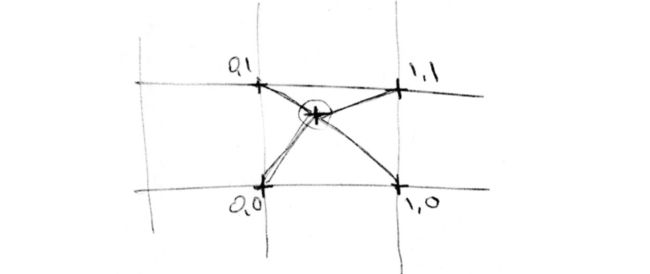
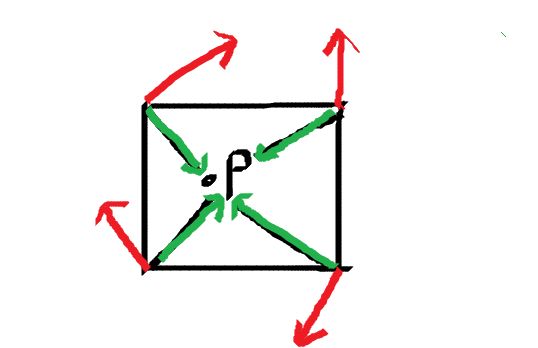
Perlin Noise (柏林噪声) 是由 Ken Perlin 发明的自然噪声生成算法。简单来说,将空间划分成大小相同的格子。对于一个输入点 (x, y),取该点所在格子的每个顶点的梯度向量与顶点到该点的方向向量的点乘,作为一个顶点对于该点的贡献值。最后使用类似 Value Noise 的插值方式计算出输入点的值。
下图中的红色向量即是每个顶点的梯度,绿色向量是四个顶点到输入位置的方向向量。对于梯度,可以使用预先计算的梯度表,也可以使用随机函数计算出一个随机的二维向量。
为了简单,这里使用随机方法生成顶点的梯度。完整代码如下:
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
vec2 random2(vec2 pos) {
vec2 vec = vec2(dot(pos, vec2(12.9898,78.233)));
return -1.0 + 2.0 * fract(sin(vec) * 43758.5453123);
}
float grad(vec2 vert, vec2 pos) {
return dot(random2(vert), pos - vert);
}
vec2 smooth(vec2 t) {
return t * t * t * (t * (6.0 * t - 15.0) + 10.0);
}
float perlinNoise(in vec2 st) {
vec2 s = smooth(fract(st));
float tl = grad(vec2(floor(st.x), ceil(st.y)), st);
float tr = grad(vec2(ceil(st.x), ceil(st.y)), st);
float bl = grad(vec2(floor(st.x), floor(st.y)), st);
float br = grad(vec2(ceil(st.x), floor(st.y)), st);
float t = mix(tl, tr, s.x);
float b = mix(bl, br, s.x);
return mix(b, t, s.y);
}
void main() {
vec2 st = gl_FragCoord.xy / u_resolution.xy;
st *= 10.0;
float n = perlinNoise(st) + 0.5;
gl_FragColor = vec4(vec3(n), 1.0);
}
最终生成的噪声图效果如下。
参考资料:
- [1] The Book of Shaders
- [2] Perlin noise - Wikipedia