【概念解析】全面理解经典协同过滤在推荐系统中的应用
全面理解经典协同过滤在推荐系统中的应用
王喆老师在的《深度学习推荐系统》一书中提到过,即使在深度学习空前流行的今天,协同过滤、逻辑回归、因子分解机等传统推荐方法仍然可以凭借其可解释性强、硬件环境要求低、易于部署和训练的天然优势而拥有大量的应用场景,而在机器学习过程中,我记得大概是学到SVD奇异值分解那一块儿的时候,《机器学习实战》一书中也为大家做过一个简单的基于物品协同过滤推荐的案例(想了一下,好像没法过,我还是放在最后面吧)。这也就是说如果我们想要深入的去探索推荐系统的话同时也需要对这些早期的传统推荐模型有所了解和学习。甚至说,很多时候将深度学习模型结合于早起推荐系统模式会产生出更好的模型也说不定。笔者所在的课题组的一位博士师姐,就将卷积(CNN)同因子分解(FM)相结合发了一篇相当不错的SCI期刊。所以我们还是要好好从基础开始,脚踏实地走好每一步。
协同过滤的地位
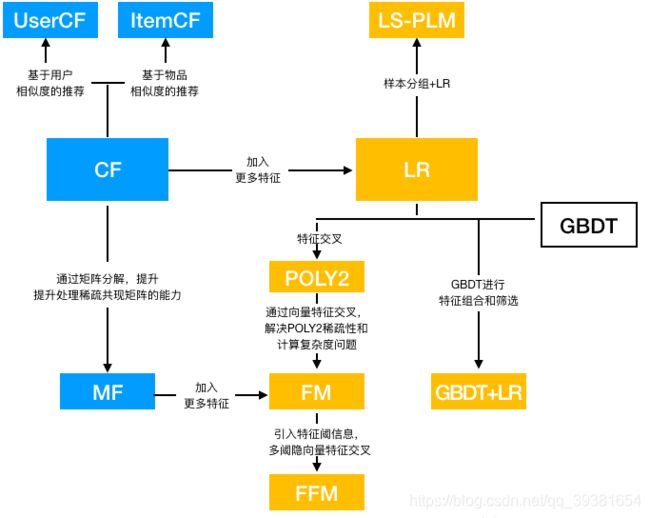
想了解协同过滤的作用和地位的话我们先来看一张图:
可以看到,协同过滤算法族(CF族)位于最开始的部分,只有出度没有入度,所以我们可以知道协同过滤算法其实是最早使用的推荐算法。曾经的推荐系统在最早的时候首选使用的就是协同过滤算法,从物品的相似度和用户相似度的角度出发,协同过滤算法衍生出了两个分支基于item的协同过滤和基于user的协同过滤两种方法。后来为了能够更好的增强模型的泛化能力同时为了能更好的处理稀疏共现矩阵问题从协同过滤中衍生出了矩阵分解模型(MF),并且在MF的基础上又衍生出了后来的因子分解机模型(MF),并诞生了很多其他后续高效模型。(这些我会在本系列的文章中给出详细的介绍)
Actually,从1992年开始协同过滤就诞生了,最初处理的问题是邮件过滤问题,不过后来亚马逊发现这种方法很适合拿来给用户推荐商品,于是才有了后来大家对协同过滤系统的标准认知。
什么是协同过滤
先简单地概括,协同过滤其实就是通过将用户和其他用户的数据进行对比来实现推荐的方法。就是协同大家的反馈、评价和意见以其对海量信息进行过滤,从中筛选出目标用户可能感兴趣的信息推荐过程。这里用一个商品推荐的例子来说明协同过滤的过程(书上的经典例子我直接拿来说事了):
- 图片a表示我们目前的数据集当中有四件物品:游戏机、小说、杂志和电视机。我们接下来要针对这些物品展开推荐。
- 图片b表示用户X访问了该网站,那么网站现在就要判断应该讲什么样的商品推荐给该用户,显然我们可以在图中看出,该用户并非第一次访问该网站,他在先前已经有过对其他物品的评价。而且我们也可以利用其他用户对其他物品的评价来参与推荐过程,图中绿色代表positive评价,而红色的代表negative评价。可以看到我们已经可以通过有向图表示出来目前已经存在过的评价体系。而且黑色粗体箭头标记出了用户X的候选推荐商品,即他还没有评价过的电视商品。接下来就要通过协同过滤去推测他对电视机会有什么倾向的评价。
- 为了方便计算,这里可以将有向图转换成矩阵的形式来进行相似度计算,在图c中行代表用户,商品作为列,将绿色赞记作数字1,将红色踩记作数字-1,将未评价记作0填充。这样就生成了共现矩阵。
- 生成共现矩阵之后接下来就是要想办法去计算用户和其他用户的相似度,来找出与目标用户X兴趣相似的用户群体集合n,然后综合这些相似用户对于电视机的评价,得出X对电视机的评价结果预测。
- 由图e可以看出(这个数据集比较简单直接观察就可以,但是其他的大型数据集就要去计算相似度来找出相似集合了)用户b和用户c与X的向量是相似的,而用户b和用户c对电视机都评价了“踩”。
- 由于相似用户对于电视机的评价都是negative,所以我们有理由推测X可能也会对电视机给出负面评价,那么在实际情况中,推荐系统不会向用户推荐电视机这个物品。
协同过滤的分类及应用场景
是的,协同过滤可以分为两个方向的协同过滤,一种是基于用户的协同过滤UserCF,另一种是基于物品的ItemCF,两种协同过滤算法的应用场景和具体实现都略有不同,但都是基于计算相似度来实现推荐的本质。
首先来说,UserCF基于用户相似度进行推荐,使其具备更强的社交特性,用户能够快速得知与自己兴趣想死的人最近喜欢的是什么,即加入以前有一个物品不在自己的兴趣范围内,也可以通过朋友动态快速的更新自己的推荐列表。这样的特点使其非常适合新闻推荐场景。因为新闻本身的兴趣点往往是分散的,相比用户对不同新闻的兴趣偏好,新闻的及时性、热点性往往是其更重要的属性,而UserCF非常适合发现热点,以及跟踪热点趋势。
其次,ItemCF是更适用于用户兴趣变化比较稳定的产品应用场景,比如电商场景,用户在一个时间段内更倾向于去寻找同类型的商品,这时候使用基于物品相似度的协同过滤推荐算法就显得更加契合于用户的购买动机,同理在一些视频推荐网站或者音乐推荐的场景当中,及时性和热点性的需求并不是很高,用户更需要推荐爱你的事兴趣偏好以内的Item,也就是说兴趣往往比较稳定,这些场景就更适合使用ItemCF。
最后,我再总结一下二者选取的一些主客观原因,其实,大家也可以发现在互联网大的应用场景下,用户数量往往会非常高,而一个系统内的商品的个数却往往比较有限(相对于用户数量来说的话)。但是UserCF却需要去维护庞大的用户相似度矩阵以便每时每刻都能快速寻找出TopN相似用户。这样来看的话代价是非常大的,大到难以承受(这是一个随着用户基数而呈n²速度的增长)。而且,用户的历史数据往往非常稀疏,对于只有几次购买或者点击行为的用户来说,找到相似的用户难度是非常大的。这导致UserCF无法应用于那些正反馈获取比较困难的场景。所以无论是亚马逊还是Netflix最初都没有使用过UserCF而是一上来就选择了ItemCF,显然通过计算共现矩阵种物品列向量的相似度来得到物品的相似矩阵要比计算User的容易不少。
关于相似度计算
刚刚,我们在前面的介绍中说过,如果数据集规模比较大无法通过直观观察找到所有相似的对象。就需要对评价目标(user或者item进行)相似度计算,来找到与推荐目标X的n个相似对象的集合。常用的几种相似度计算方式包括欧氏距离、余弦相似度、皮尔逊相关系数。(这三种相似度计算方法事实上在大家机器学习对奇异值分解那一章的学习过程中就已经学习过了)
首先看一下余弦相似度计算方法:(这里给出代码的实现方式)
# 余玄相似度 根据公式带入即可,其中分母为二范数计算函数,linalg的norm可计算二范数
def cosSim(inA, inB):
num = float(inA.T * inB)
denom = la.norm(inA) * la.norm(inB)
return 0.5 + 0.5 * (num / denom) 这种相似度的计算方法非常好理解,就是去使用余弦相似度来计算向量间的相似度,也就是说夹角余弦值可以作为衡量相似度的手段,夹角越小,证明余弦相似度越大,两个用户或者两个物品相似度越大。
然后,再介绍一种更简单的相似度计算方法,那就是欧式距离计算法。即直接把两个向量在特征空间的欧氏距离表达为相似度,显然距离越小越相似,代码如下:
# 欧式距离这里返回结果已处理 0,1 0最大相似,1最小相似 欧氏距离转换为2范数计算
def ecludSim(inA, inB):
return 1.0 / (1.0 + la.norm(inA - inB))第三种相似度计算方法更为精确一些,叫做皮尔逊相关系数法,相比于余弦相似度,皮尔逊相关系数通过使用用户平均分对各独立评分进行修正,减少了用户评分bias的影响。要更精确一些。
# 皮尔逊相关系数 numpy的corrcoef函数计算
def pearsSim(inA, inB):
if (len(inA) < 7):
return 1.0
return 0.5 + 0.5 * corrcoef(inA, inB, rowvar=0)[0][1] # 使用0.5+0.5*x 将-1,1 转为 0,1排序返回TopN
在获取了物品或者用户相似度信息之后,就要对相似度开始进行排序,利用TopN生成最终的推荐结果,TopN的生成过程中常用的得分计算方式其实很简单,拿UserCF来举例的话:
可以通过公式看出,公式是利用用户相似度和相似用户的评价的加权平均来获得目标用户的评价预测。其中,权重wu,s是用户u和用户s的相似度,Rs,p是用户s对物品p的评分。当通过该公式计算出得分之后再根据得分排序就可以得到TopN推荐序列了。
(不偷懒了,再补上ItemCF的公式吧)
其中,H是目标用户的正反馈物品集合,wp,h是物品p与物品h的物品相似度,Ru,h是用户u对物品h的已有评分。
协同过滤的局限性
协同过滤非常直观,而且可解释性强,但是它仍然具有很多的局限性,比如它的泛化能力比较差,协同过滤无法将两个物品相似这一信息推广到其他物品的相似度计算上。这就到这了一个严重的问题,热门物品具有很强的头部效应,容易跟大量的商品产生相似度,而长尾商品,由于其特征向量稀疏,很少与其他物品产生相似度,导致被推荐的可能性很小。但是去发掘长尾商品,增加长尾被推荐的可能性却是推荐系统最重要的目标之一。这其实也可以被视为是协同过滤的天然缺陷,本身无论是基于用户还是基于商品,协同过滤对稀疏向量的处理本身就很弱,所以头部效应才会这么明显。
也正是因此,才有矩阵分解技术MF被提了出来,它可以解决上述问题,并且增加泛化能力。这个我们放到下篇文章来讲。
协同过滤还有其他的局限性,比如,CF方法其实只是利用了用户和物品之间的交互信息,却无法去考虑以及综合其他的语义信息,比如年龄,性别,商品描述,商品分类等等。这会导致对数据的挖掘不够彻底,造成信息的遗漏。
正是因为这个原因,逻辑回归模型为核心的模型才会发展起来,能够综合不同类型特征的机器学习模型才能够大放异彩,我们同样放到后面来讲。
关于一个经典案例的实现
关于协同过滤算法和它的内容先讲到这里,接下来是我之前提到的那个小案例,大家可以实验一下来看看CF究竟是怎样运作的:
# Author:JinyuZ1996
# Creation date:2020/7/14 12:21
from numpy import *
from numpy import linalg as la
# 样本矩阵维度为(用户7x商品5)
# 矩阵中为零的元素为0表示该用户未评价此商品,即可以作为推荐商品
def loadExData():
return [[4, 4, 0, 2, 2],
[4, 0, 0, 3, 3],
[4, 0, 0, 1, 1],
[1, 1, 1, 2, 0],
[2, 2, 2, 0, 0],
[1, 1, 1, 0, 0],
[5, 5, 5, 0, 0]]
# 我们和我们李航老师的书上统一一下,假定导入数据都为列向量,若行向量则需要对代码简单修改
# 欧式距离这里返回结果已处理 0,1 0最大相似,1最小相似 欧氏距离转换为2范数计算
def ecludSim(inA, inB):
return 1.0 / (1.0 + la.norm(inA - inB))
# 皮尔逊相关系数 numpy的corrcoef函数计算
def pearsSim(inA, inB):
if (len(inA) < 7):
return 1.0
return 0.5 + 0.5 * corrcoef(inA, inB, rowvar=0)[0][1] # 使用0.5+0.5*x 将-1,1 转为 0,1
# 余玄相似度 根据公式带入即可,其中分母为2范数计算,linalg的norm可计算范数
def cosSim(inA, inB):
num = float(inA.T * inB)
denom = la.norm(inA) * la.norm(inB)
return 0.5 + 0.5 * (num / denom) # 同样操作转换 0,1
# 对物品评分 (数据集 用户行号 计算误差函数 推荐商品列号)
def standEst(dataMat, user, simMeas, item):
n = shape(dataMat)[1] # 获得特征列数
simTotal = 0.0;
ratSimTotal = 0.0 # 两个计算估计评分值变量初始化
for j in range(n):
userRating = dataMat[user, j] # 获得此人对该物品的评分
if userRating == 0: # 若此人未评价过该商品则不做下面处理
continue
# 变量overlap时给出了两个物品中已经被评分的那个元素(目的是发掘两个用户都评级过的物品)
overLap = nonzero(logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0] # 获得相比较的两列同时都不为0的数据行号
if len(overLap) == 0:
similarity = 0
else:
# 求两列的相似度
similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j]) # 利用上面求得的两列同时不为0的行的列向量 计算距离
simTotal += similarity # 计算总的相似度
ratSimTotal += similarity * userRating # 不仅仅使用相似度,而是将评分当权值*相似度 = 贡献度
if simTotal == 0: # 若该推荐物品与所有列都未比较则评分为0
return 0
else:
return ratSimTotal / simTotal # 归一化评分 使其处于0-5(评级)之间
# 给出推荐商品评分产生最高的N个推荐结果(数据矩阵,用户编号,默认是三个(我设的,你可以自己改),相似度算法,估计算法)
def recommend(dataMat, user, N=2, simMeas=ecludSim, estMethod=standEst):
unratedItems = nonzero(dataMat[user, :].A == 0)[1] # 找到该行所有为0的位置(即此用户未评价的商品,才做推荐)
if len(unratedItems) == 0:
return '所有物品都已评价,无可推荐选项'
itemScores = []
for item in unratedItems: # 循环所有没有评价的商品列下标
estimatedScore = estMethod(dataMat, user, simMeas, item) # 计算当前产品的评分
itemScores.append((item, estimatedScore))
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N] # 将推荐商品排序
# 结果测试如下:
myMat = mat(loadExData())
# 对第三个用户进行默认推荐
result1 = recommend(myMat, 2) # 参数:数据集,用户编号2(就是第三个人),默认推荐2个物品,欧氏距离,估计方法
print(result1)
# 对第三个用户只推荐一件商品
result2 = recommend(myMat, 2, 1)
print(result2)
# 对照组设计(不同的相似度计算算法1)
result3 = recommend(myMat, 2, simMeas=pearsSim) # 相似度方法改为相关系数
print(result3)
# 对照组设计(不同的相似度计算算法2)
result4 = recommend(myMat, 2, simMeas=cosSim) # 相似度方法改为夹角余弦系数
print(result4)
# 对第四个用户默认推荐(第四个用户只有一件商品没评价过所以结果也是推荐一件)
result5 = recommend(myMat, 3, simMeas=cosSim) # 相似度方法改为夹角余弦
print(result5)
这是今年7月份学习统计学习方法的时候写的小案例了,参考的是《机器学习实战》的构建方法,诸事还算详细,大家凑活着看吧,后面会继续给大家写其他的推荐模型和算法的文章,继续学习,不断总结。