回归模型汇总、评估和总结

回归模型汇总、评估和总结

在本篇您将学到：
  ● 回归类任务的基本解决方法
  ● 针对任务数据集的特征工程
  ● 回归模型的使用和调参
  ● 基础模型与树模型的实验对比分析
本篇包含的回归模型有
    LinearRegression：线性回归模型、
    Ridge：岭回归模型 、
    Lasso：Lasso回归模型 、
    ElasticNet：弹性网络回归，岭回归和Lasso回归的混合模型、
    SVR：支持向量回归 、
    GradientBoostingRegressor：GB梯度提升回归模型
    XGBoost、LightGBM、CatBoost、NGBoost：四大树的回归模型

---

I 库

在一般的Anaconda环境下，还需要pip安装如下两个包：
  mlxtend：堆叠回归模型
  ngboost：斯坦福吴恩达团队提出NGBoost：用于概率预测的自然梯度提升，这个模型除了慢了点，在与xgboost、lightgbm、catboost三大经典树模型比较下，其回归效果最好。

pip install mlxtend -i https://pypi.douban.com/simple
pip install ngboost -i https://pypi.tuna.tsinghua.edu.cn/simple

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

from scipy.special import boxcox1p
from scipy.stats import skew,boxcox_normmax


from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error,mean_squared_error,explained_variance_score,median_absolute_error,r2_score
from sklearn.preprocessing import MinMaxScaler,StandardScaler,RobustScaler

from sklearn.svm import SVR
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.linear_model import LinearRegression,RidgeCV,LassoCV,ElasticNetCV
from mlxtend.regressor import StackingCVRegressor # pip install mlxtend -i https://pypi.douban.com/simple
from lightgbm import LGBMRegressor
from xgboost import XGBRegressor
from catboost import CatBoostRegressor
from ngboost import NGBRegressor
from ngboost.ngboost import NGBoost # pip install ngboost -i https://pypi.tuna.tsinghua.edu.cn/simple
from ngboost.learners import default_tree_learner
from ngboost.distns import Normal

II 数据

data = pd.read_csv('../data/train.csv')
print('缺省值：',data.isna().sum().sum())
data.head()

为保证隐私安全，具体数据不再透漏，大家在实验或比赛时仅需使用自己的回归数据即可

划分数据集为训练集和测试集

train_x, test_x, train_y, test_y = train_test_split(X, Y, test_size=0.25,random_state=2020)

III 默认参数

3.1 导入各类回归模型

lr = LinearRegression()
ridge = Ridge()
lasso = Lasso()
enet  = ElasticNet()
xgb = XGBRegressor()
lgb = LGBMRegressor()
cat = CatBoostRegressor()
ngb = NGBRegressor()

3.2 模型训练

lr.fit(train_x,train_y)
ridge.fit(train_x,train_y)
lasso.fit(train_x,train_y)
enet.fit(train_x,train_y)
xgb.fit(train_x,train_y,verbose=False)
lgb.fit(train_x,train_y,verbose=False)
cat.fit(train_x,train_y,verbose=False)
ngb.fit(train_x,train_y)

3.3 模型预测

lr_pre    = lr.predict(test_x)
ridge_pre = ridge.predict(test_x)
lasso_pre = lasso.predict(test_x)
enet_pre  = enet.predict(test_x)
xgb_pre   = xgb.predict(test_x)
lgb_pre   = lgb.predict(test_x)
cat_pre   = cat.predict(test_x)
ngb_pre   = ngb.predict(test_x)

3.4 模型评估

# MAE 平均绝对值误差 
## 用于评估预测结果和真实数据集的接近程度的程度，其其值越小说明拟合效果越好
# MSE 均方差
## 该指标计算的是拟合数据和原始数据对应样本点的误差的平方和的均值，其值越小说明拟合效果越好。
# MedianAE 中值绝对误差
## 此种方法非常适应含有离群点的数据集,越小越好

# EVS 可释方差得分
## 解释回归模型的方差得分，其值取值范围是[0,1]，越接近于1说明自变量越能解释因变量的方差变化，值越小则说明效果越差。
# R2  决定系数（拟合优度）
## 判定系数，其含义是也是解释回归模型的方差得分，其值取值范围是[0,1]，越接近于1说明自变量越能解释因变量的方差变化，值越小则说明效果越差。

mae  = []
mse  = []
median_ae = []

evs  = []
r2   = []
all_less = []
all_more = []
for pre,name in zip([lr_pre,ridge_pre,lasso_pre,enet_pre,xgb_pre,lgb_pre,cat_pre,ngb_pre],
                   ['lr','ridge','lasso','enet','xgb','lgb','cat','ngb']):
    print(name,':')
    MAE = mean_absolute_error(test_y,pre)
    MSE = mean_squared_error(test_y,pre)
    EVS = explained_variance_score(test_y,pre)
    Median_AE = median_absolute_error(test_y,pre)
    R2  = r2_score(test_y,pre)
    mae.append(MAE)
    mse.append(MSE)
    evs.append(EVS)
    median_ae.append(Median_AE)
    r2.append(R2)
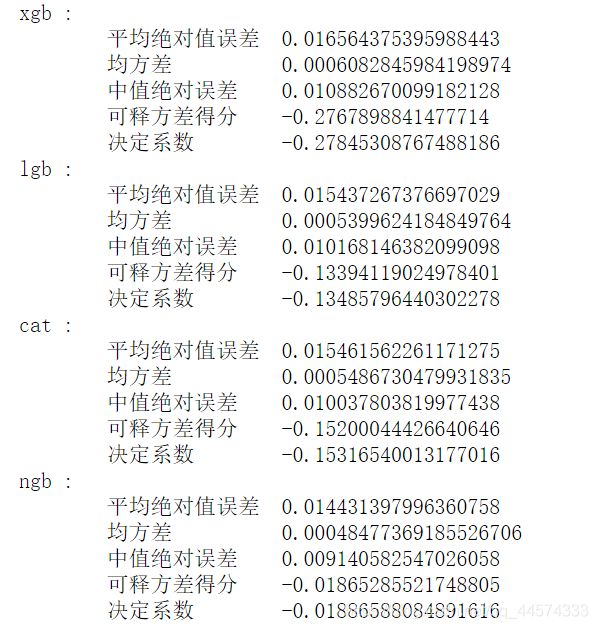
    print('\t平均绝对值误差\t{}\n\t均方差 \t\t{}\n\t中值绝对误差 \t{}\n\t可释方差得分 \t{}\n\t决定系数 \t{}'.format(
    MAE,MSE,Median_AE,EVS,R2))

数据是冷漠的，还是让我们来看一下对比图

y_plot = mae
x_name = ['lr','ridge','lasso','enet','xgb','lgb','cat','ngb']

plt.figure(figsize=(15,10), dpi=80)

plt.subplot(221)
plt.ylim(0.014,0.016)
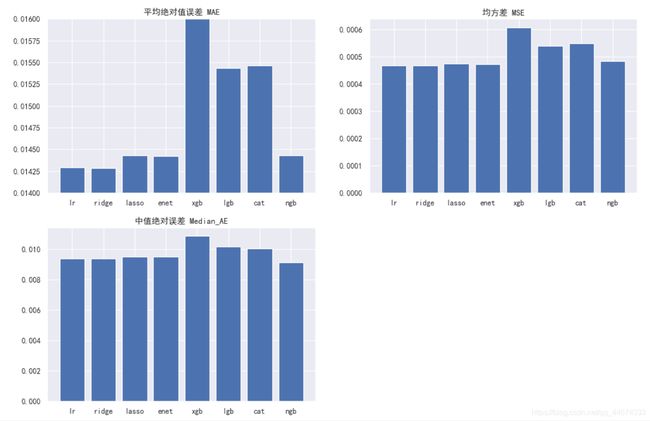
plt.title('平均绝对值误差 MAE')
plt.bar(x_name,y_plot)

y_plot = mse
plt.subplot(222)
# plt.ylim(0.014,0.016)
plt.title('均方差 MSE')
plt.bar(x_name,y_plot)

y_plot = median_ae
plt.subplot(223)
# plt.ylim(0.014,0.016)
plt.title('中值绝对误差 Median_AE')
plt.bar(x_name,y_plot)

3.5 结论

在默认参数、无任何特征工程的情况下，可以看出各回归模型的效果：
  ridge >= lr > enet > lasso > ngb > lgb > cat > xgb

有趣的是，我们的基础模型在这种朴素的情况下效果都不错，而三大经典树模型 xgb、lgb、cat的回归效果却较差，但值得一提的是NGBoost还是有着与基础模型中的enet、lasso一样不错的效果的。

IV 特征工程

对于这份数据，因为其数据均为数值特征，故笔者在此仅考虑了一种对数值特征有普适性通用的特征工程，数据规范化，但规范化又有很多种，在此，我们考虑两种常见的规范化:

1. MinMaxScaler: 归一到 [ 0，1 ]
2. StandardScaler: 通过删除平均值和缩放到单位方差来标准化特征

同样通过模型回归效果来决定该选择哪一种

def choose_scaler(model_name,X):
    """
    model_name = ['lr','ridge','xgb','lgb']
    return MAE 和 图
    """
    min_max_scaler  = MinMaxScaler().fit(X)
    standard_scaler = StandardScaler().fit(X)
    
    X_minmax   = min_max_scaler.transform(X) 
    X_standard = standard_scaler.transform(X)
    
    if model_name == 'lr':
        print('（MAE） LR:\t0.014288303965603513')
        
        train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
        lr.fit(train_x,train_y)
        minmax = mean_absolute_error(test_y,lr.predict(test_x))
        print('MinMax规范化:  ',minmax)
        train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
        lr.fit(train_x,train_y)
        standard = mean_absolute_error(test_y,lr.predict(test_x))
        print('Standard规范化:',standard)
        plt.bar(['LR','MinMax规范化','Standard规范化:'],[0.014288303965603513,minmax,standard])
    elif model_name == 'xgb':
        print('（MAE） XGB:\t0.016564375395988443')
        
        train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
        xgb.fit(train_x,train_y,verbose=False)
        minmax = mean_absolute_error(test_y,xgb.predict(test_x))
        print('MinMax规范化:  ',minmax)
        train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
        xgb.fit(train_x,train_y,verbose=False)
        standard = mean_absolute_error(test_y,xgb.predict(test_x))
        print('Standard规范化:',standard)
        plt.bar(['XGB','MinMax规范化','Standard规范化:'],[0.016564375395988443,minmax,standard])
    elif model_name == 'ridge':
        print('（MAE） Ridge:\t0.0142876509355531')
        
        train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
        ridge.fit(train_x,train_y)
        minmax = mean_absolute_error(test_y,ridge.predict(test_x))
        print('MinMax规范化:  ',minmax)
        train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
        ridge.fit(train_x,train_y)
        standard = mean_absolute_error(test_y,ridge.predict(test_x))
        print('Standard规范化:',standard)
        plt.bar(['Ridge','MinMax规范化','Standard规范化:'],[0.0142876509355531,minmax,standard])
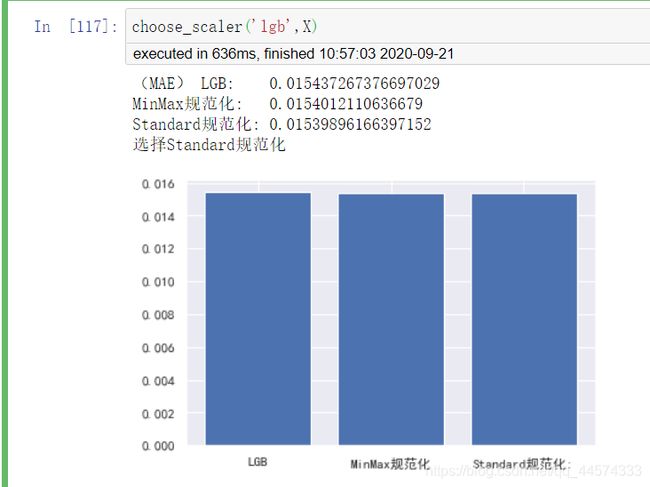
    elif model_name == 'lgb':
        print('（MAE） LGB:\t0.015437267376697029')
        
        train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
        lgb.fit(train_x,train_y,verbose=False)
        minmax = mean_absolute_error(test_y,lgb.predict(test_x))
        print('MinMax规范化:  ',minmax)
        train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
        lgb.fit(train_x,train_y,verbose=False)
        standard = mean_absolute_error(test_y,lgb.predict(test_x))
        print('Standard规范化:',standard)
        plt.bar(['LGB','MinMax规范化','Standard规范化:'],[0.015437267376697029,minmax,standard])
    if minmax<standard:print('选择MinMax规范化')
    else:print('选择Standard规范化')

4.1 基础模型lr

先看我们的基础模型lr对两种规范化的选择

choose_scaler('lr',X)
# Standard规范化

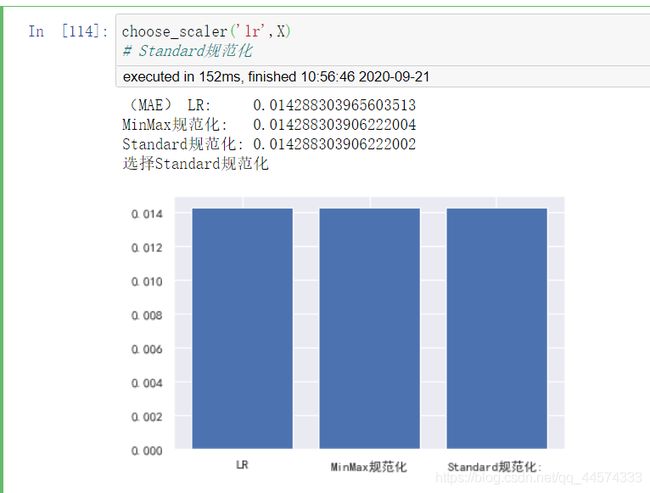
对于lr而言，两者效果类似，且都比不做规范化效果好。差别不大，但Standard的模型效果更好。

lr选择StandardScaler。

4.2 基础模型ridge

choose_scaler('ridge',X)

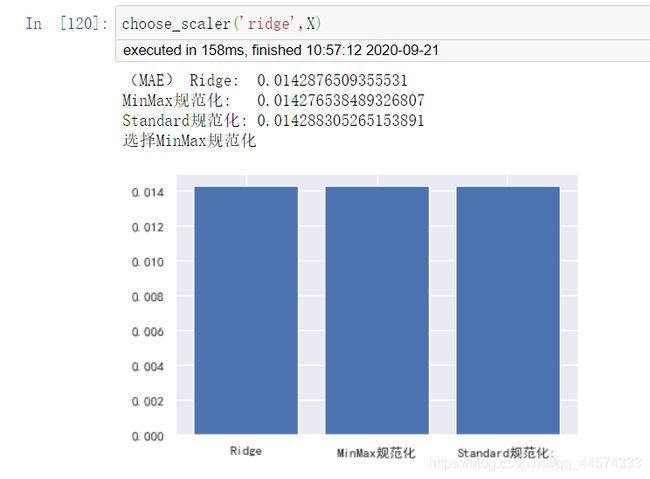
对于ridge而言，两者效果还是有一定差异的，且Standard后模型效果反而变差了一点。

ridge选择MinMaxScaler。

4.3 树模型XGBoost

再让我们看看树模型对于俩种规范化的选择

choose_scaler('xgb',X)

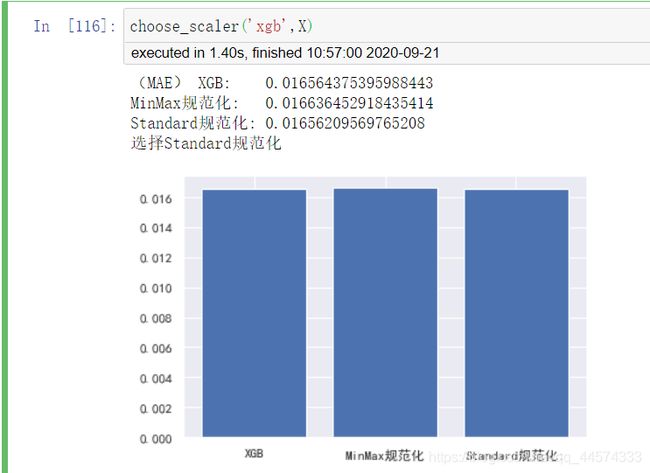
对于树模型xgb而言，MinMax后模型效果变差，但Standard后模型效果反而变好。和线性模型相比这个实验结果正好相反，这还是很有趣的。

xgb选择StandardScaler。

4.4 树模型Lightgbm

choose_scaler('lgb',X)

同样对于树模型lgb也选择StandardScaler。

综上，笔者最终选择了StandardScaler来规范化数据。

X_standard = pd.DataFrame(standard_scaler.transform(X),columns=X.columns)

V 调参模型

5.1 模型的定义、调参

各种回归模型的定义、调参请参见代码

#定义LR回归模型
# LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
# fit_intercept:是否有截据，如果没有则直线过原点;
# normalize:是否将数据归一化;
# copy_X:默认为True，当为True时，X会被copied,否则X将会被覆写;
# n_jobs:默认值为1。计算时使用的核数
# 无调参
lr = LinearRegression()

#定义ridge岭回归模型（使用二范数作为正则化项。不论是使用一范数还是二范数，正则化项的引入均是为了降低过拟合风险。）
#注：正则化项如果使用二范数，那么对于任何需要寻优的参数值，在寻优终止时，它都无法将某些参数值变为严格的0，尽管某些参数估计值变得非常小以至于可以忽略。即使用二范数会保留变量的所有信息，不会进行类似PCA的变量凸显。
#注：正则化项如果使用一范数，它比L2范数更易于获得“稀疏(sparse)”解，即它的求解结果会有更多的零分量。
alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5]
alphas2 = [5e-05, 0.0001, 0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007, 0.0008]
e_alphas = [0.0001, 0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007]
e_l1ratio = [0.8, 0.85, 0.9, 0.95, 0.99, 1]

ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt))

#定义LASSO收缩模型（使用L1范数作为正则化项）（由于对目标函数的求解结果中将得到很多的零分量，它也被称为收缩模型。）
#注：正则化项如果使用二范数，那么对于任何需要寻优的参数值，在寻优终止时，它都无法将某些参数值变为严格的0，尽管某些参数估计值变得非常小以至于可以忽略。即使用二范数会保留变量的所有信息，不会进行类似PCA的变量凸显。
#注：正则化项如果使用一范数，它比L2范数更易于获得“稀疏(sparse)”解，即它的求解结果会有更多的零分量。
lasso = make_pipeline(RobustScaler(), LassoCV(max_iter=1e7, alphas=alphas2, random_state=42))

#定义elastic net弹性网络模型（弹性网络实际上是结合了岭回归和lasso的特点，同时使用了L1和L2作为正则化项。）
enet = make_pipeline(RobustScaler(), ElasticNetCV(max_iter=1e7, alphas=e_alphas, l1_ratio=e_l1ratio))

#定义SVM支持向量机模型                                     
svr = make_pipeline(RobustScaler(), SVR(C= 20, epsilon= 0.008, gamma=0.0003,))

#定义GB梯度提升模型（展开到一阶导数）
gbr = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.05, max_depth=4, max_features='sqrt', min_samples_leaf=15, min_samples_split=10, loss='huber', random_state =42)                             

#定义lightgbm模型
lgb= LGBMRegressor(objective='regression', 
                                       num_leaves=4,
                                       learning_rate=0.01, 
                                       n_estimators=5000,
                                       max_bin=200, 
                                       bagging_fraction=0.75,
                                       bagging_freq=5, 
                                       bagging_seed=7,
                                       feature_fraction=0.2,
                                       feature_fraction_seed=7,
                                       verbose=-1,
                                       #min_data_in_leaf=2,
                                       #min_sum_hessian_in_leaf=11
                                       )

#定义xgboost模型（展开到二阶导数）                                      
xgb = XGBRegressor(learning_rate=0.01, n_estimators=3460,
                                     max_depth=3, min_child_weight=0,
                                     gamma=0, subsample=0.7,
                                     colsample_bytree=0.7,
                                     # objective='reg:linear', nthread=-1,
                                     objective='reg:squarederror', nthread=-1,
                                     scale_pos_weight=1, seed=27,
                                     reg_alpha=0.00006)

#定义catboost模型
cat =  CatBoostRegressor(iterations=700,learning_rate=0.02,
                         depth=12,eval_metric='MAE',random_seed = 23,
                         bagging_temperature = 0.2,od_type='Iter',verbose=False)

# 定义ngboost模型
ngb = NGBRegressor(Base=default_tree_learner, Dist=Normal,  natural_gradient=True,verbose=False)

5.2 集成模型

在此，笔者还加了一种集成模型

# #集成多个个体学习器
# 这里我仅保留了最好的四大基础模型和一个最好的树模型ngb，下图也证实了模型的效果
stack_gen = StackingCVRegressor(regressors=(lr,ridge,lasso,enet,ngb),
                                meta_regressor=ngb,
                                use_features_in_secondary=True)

5.3 模型效果

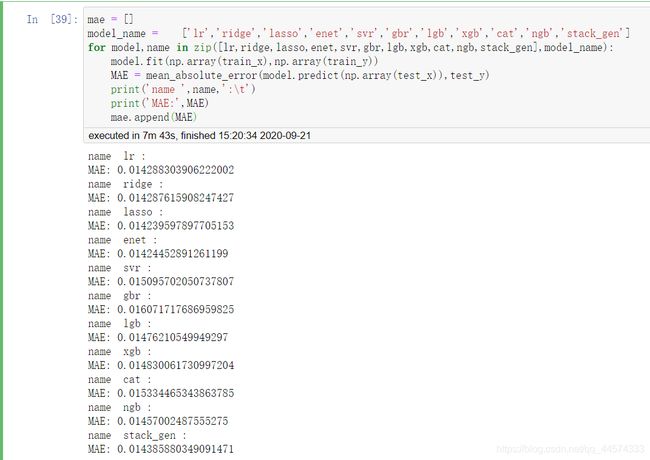
mae = []
model_name =    ['lr','ridge','lasso','enet','svr','gbr','lgb','xgb','cat','ngb','stack_gen']
for model,name in zip([lr,ridge,lasso,enet,svr,gbr,lgb,xgb,cat,ngb,stack_gen],model_name):
    model.fit(np.array(train_x),np.array(train_y))
    MAE = mean_absolute_error(model.predict(np.array(test_x)),test_y)
    print('name ',name,':\t')
    print('MAE:',MAE)
    mae.append(MAE)

sns.set()
plt.figure(figsize=(10,5))
plt.ylim(0.014,0.016)
plt.title('M A E')
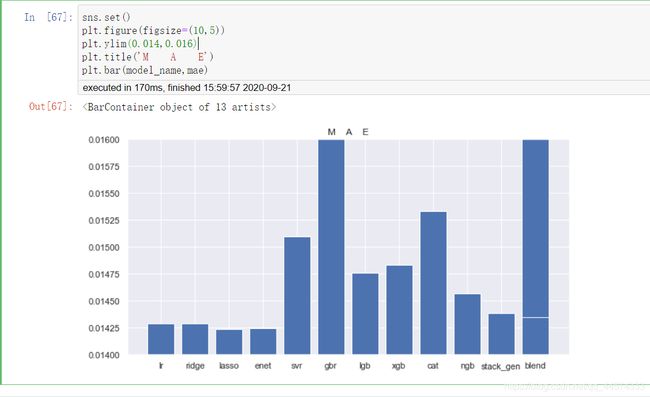
plt.bar(model_name,mae)

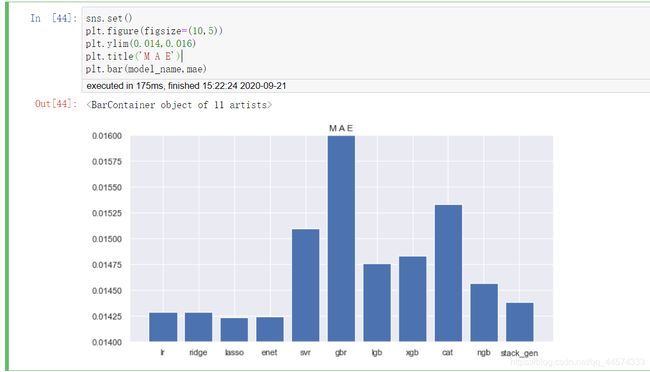
由上图可知：
在对数据规范后，回归模型的效果如下：
  lasso >= enet > ridge >= lr > stack_gen > ngb > lgb > xgb > svr > cat > gbr

5.4 模型融合

最后，笔者使用了一种加权组合的方法融合了所有模型

w = [1/i for i in mae]
w = [i/sum(w) for i in w]
# 综合多个模型产生的预测值，作为多模型组合学习器的预测值
lr    = lr.fit(train_x,train_y)
ridge = ridge.fit(train_x,train_y)
lasso = lasso.fit(train_x,train_y)
enet  = enet.fit(train_x,train_y)
svr   = svr.fit(train_x,train_y)
gbr   = gbr.fit(train_x,train_y)
lgb   = lgb.fit(train_x,train_y)
xgb   = xgb.fit(train_x,train_y)
cat   = cat.fit(train_x,train_y)
ngb   = ngb.fit(train_x,train_y)
stack_gen = stack_gen.fit(train_x,train_y)

def blend_models_predict(test_x):
    return (
            lr.predict(test_x)      * w[0]+
            ridge.predict(test_x)   * w[1]+
            lasso.predict(test_x)   * w[2]+
            enet.predict(test_x)    * w[3]+
            svr.predict(test_x)     * w[4]+
            gbr.predict(test_x)     * w[5]+
            lgb.predict(test_x)     * w[6]+
            xgb.predict(test_x)     * w[7]+
           cat.predict(test_x)      * w[8]+
           ngb.predict(test_x)      * w[9]+
           stack_gen.predict(np.array(test_x)) * w[10] 
           )
blend_all_pre = blend_models_predict(test_x)


mae.append(mean_absolute_error(blend_all_pre,test_y))
model_name.append('blend')

sns.set()
plt.figure(figsize=(10,5))
plt.ylim(0.014,0.016)
plt.title('M    A    E')
plt.bar(model_name,mae)

VI 总结

注：本实验的结论仅是针对该数据集的结论。

本次实验的实验目的是测试各类回归模型对于该数据集的回归效果，找出最适合该数据集的回归模型进行实际应用。

（1）在无特征工程+默认参数的情况下，我们得到了如下的模型效果：
  ● ridge >= lr > enet > lasso > ngb > lgb > cat > xgb
可以看出，“朴素简单”的基础模型是很值得肯定的，不仅训练时间短，在这种情况下效果也是超过各类先进、复杂的树模型。且在树模型中NGBoost值得一用，但其训练时间过长是一大缺憾。

（2）在数据规范化+优化调参的情况下，各类回归模型的效果如下：
  ● lasso >= enet > ridge >= lr > stack_gen > ngb > lgb > xgb > svr > cat > gbr

同样，前四名还是由四大基础模型lr、ridge、enet和lasso组成。值得一提的是，集成模型stack_gen排在了第五名，之后就是树模型。但Catboost在该数据集的回归效果不佳。
 
 
愚见：笔者在得到上述结论时是有一定疑惑的，为什么我们优秀的树模型在回归上却比不上基础模型。且在笔者查找Kaggle比赛上也发现了这一问题，很多回归比赛基础模型lr之类的本地cv确实会优于xgb，但其实和本实验一样，两者差别并不大，但还是基础模型本地cv更优，且最终topline所选择的也是笔者上面使用的stack_gen的集成模型，而非单独的基础模型或树模型。且在实际回归应用中，我们都知道xgb横行金融预测。在此，笔者认为在数据的特征工程不够完美的时候，“一树带基础模型”会更好、更稳定，之后再通过树模型不断优化将会更好。

 
 
完整ipynb代码文件请见Github：
https://github.com/AmangAris/Summary