二叉树实现原理
举例:
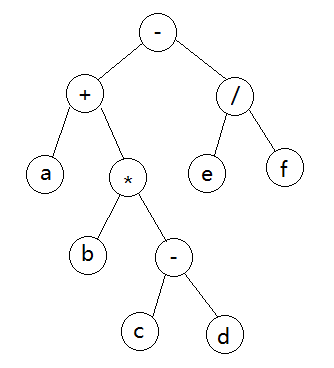
对于表达式 a+b*(c-d)-e/f 的二叉树如下:
运算符优先级判断标准:
1.加减运算符优先级低于乘除优先级;
2.括号内的运算符优先级最高;
3.当优先级相同时,位置靠后的优先级最低
具体步骤如下:
- 对字符串的运算符号进行遍历,找出优先级最低的运算符,在该字符串中,首先对‘+’进行判断,是目前优先级最低的,然后访问到'*',比'+'高,接下来'-'因为在括号内的缘故,比'+'高,然后是'-',跟'+‘一样的优先级,但是位置靠后,所以’+‘被取代,’-‘成为当前优先级最低的,接下来是'/',比'-'高。所以该结点的数据为'-'。
- 左子树则遍历 a+b*(c-d),右子树则遍历 e/f ,根据优先级递归创建二叉树。
对于正负号,发现正负号一般在数字的前面,根据递归规律,可以发现,一般正负号在字符串的第一位,后面跟着数字,由此可以将正负号当作是对其后面的数字的取值操作
函数详述
(1)树结点
typedef union
{
char symbol;
double number;
}UN;
typedef struct TREE
{
UN data; //联合结构可以节省空间
TREE *lchild;
TREE *rchild;
}Tree;
(2)checkBrackets(char input, int l, int r)
检查左右两边的括号是否为同一对,同一对则可以移除 例如:(2 + 4)(3 - 1) 是不可以去掉最左边跟最右边的括号的。若为同一对,返回true,否则返回false
bool checkBrackets(char *input, int l, int r)
{
int flag = 0;
char c;
int i;
for (i = l; i <= r; i++)
{
c = input[i];
if (c == '(')
flag++;
else if (c == ')')
flag--;
if (flag == 0)
break;
}
if ((flag == 0) && (i >= r))
return true;
else return false;
}
(3)findNode(char *input, int l, int r)
寻找下标为l~r的字符串中的优先级最低的运算符
int findNode(char *input, int l, int r)
{
int index = 0;
char data;
int flag = 0;
bool finded = false;
for (int i = l; i <= r; i++)
{
data = input[i];
switch (data)
{
case '(': flag++; break;
case ')': flag--; break;
case '+':
case '-': if (!flag && i != l){ finded = true; index = i; break; }
//i!=l : eleminite the negative number;like (- 4 / 5) ,the '/''s priority is lower than '-''s;
case '*':
case '/': if (!finded && !flag) { index = i; break; }
//There the finded can not be set to true ,when it is true,like 2*3*4 will be wrong.
}
}
return index;
}
(4)Tree *buildTrees(char *input, int l, int r)
根据表达式创建二叉树
Tree *buildTrees(char *input, int l, int r)
{
if ((input[l] == '(') && (input[r] == ')') && (checkBrackets(input, l, r)))
{
l++;
r--;
}
int i;
int index;
for (i = l; i <= r; i++)
{
if ((i == l) && ((input[i] == '-') || (input[i] == '+'))) //deal with positive and negative numbers
continue;
if (!isdigit(input[i]) && (input[i] != '.'))
break;
}
if (i >= r)
{// i>= r means the string all are numbers,it is leaf of Binary Tree
Tree *T = new Tree;
T->data.number = atol(input + l);
T->lchild = T->rchild = NULL;
return T;
}
else
{
index = findNode(input, l, r);
Tree *t = new Tree;
t->data.symbol = input[index];
t->lchild = buildTrees(input, l, index - 1);
t->rchild = buildTrees(input, index + 1, r);
return t;
}
}
(5)preOrder(Tree *tree)
根据后序遍历计算表达式结果
double preOrder(Tree *tree)
{
if (tree == NULL)
return 0;
if ((tree->lchild == NULL) && (tree->rchild == NULL))
return tree->data.number;
double lresult = preOrder(tree->lchild);
double rresult = preOrder(tree->rchild);
double result = 0.0;
switch (tree->data.symbol)
{
case '-': result = lresult - rresult; break;
case '+': result = lresult + rresult; break;
case '*': result = lresult * rresult; break;
case '/': if(rresult != 0) result = lresult / rresult; break;
}
return result;
}