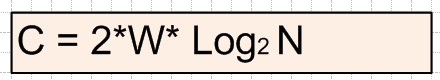星星之火-9:详解信道特性与奈奎斯特定理和香农定理
奈奎斯特定理和香农定理,结论很简单,但理解起来有点费劲,特别是结论背后的原因,本文在不进行数学推导的情况下,对此进行详细的拆解。
目录
第1章 传输信道
1. 1 信道的定义与分类
1.2 信道的衰减特性
1.3 信道频率特性与带宽
第2章 数字通信与比特率、波特率
2.1. 代表二进制的“电”符号symbol
2.2 符号率、波特率、比特率
2.3. 最大符号率、 最大符波特率、 最大符比特率
第3章 奈奎斯特(Nyquist)准则
第4章 香农定理
4.1 噪声的定义
4.2 信噪比定义
4.3 香农定理
第5章 香农定理与奈奎斯特(Nyquist)准则的关系
第1章 传输信道
1. 1 信道的定义与分类
数据传输信道是指为数据信号传输提供的通路。
(1)狭义信道,仅指传输介质本身,能够传输信号的任何抽象的或具体的通路,如电缆、光纤、微波、短波等。
(2)广义信道,包含传输介质和完成各种形式的信号变换功能的发送及接收设备,可看成是一条实际传输线路及相关设备的逻辑部件。
从不同角度对信道有多种分类方法:
(1)按照允许的信号的类型分为模拟信道和数字信道。
模拟信道只允许传输波形连续变化的模拟信号,通信质量可用失真和输出信噪比来衡量。
数字信道只允许传输离散的数字信号,数字信道的特性可用差错率及差错序列的统计特性来描述。
模拟数据和数字数据都可以用模拟信号或数字信号来表示,因而无论信源产生的是模拟数据还是数字数据,在传输过程中都可以用适合于信道传输的某种信号形式来传输。
(2)按信道的使用方法分为专用信道和公共交换信道。
专用信道是指连接两点或多点的固定线路,
公共交换信道是一种通过交换机转接可为大量用户服务的信道。
(3)按数据传输的同步方式分为同步信道和异步信道。
(4)按信道传输的信息复用形式分为频分复用信道和时分复用信道。
(5)按照信道采用的传输介质分为有线信道和无线信道。
有线信道主要有四类。即明线(open wire)、对称电缆(Symmetrical cable)、同轴电缆(coaxial cable)和光纤(Optical fiber)。
有线信道:以导线(双绞线或者光纤等)为传输媒质,信号沿导线进行传输,信号的能量集中在导线附近,因此传输效率高,但是部署不够灵活。信噪比高、频带资源窄、存在回波和非线性失真。
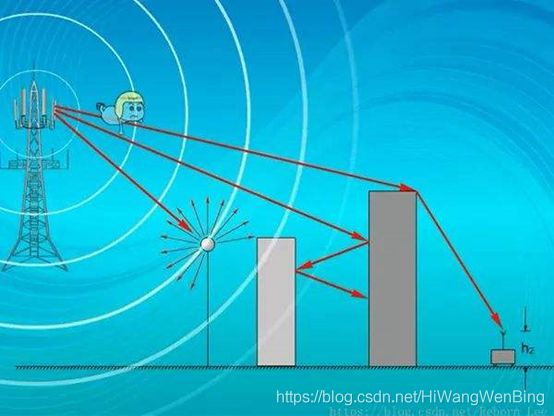
无线信道:是对无线通信中发送端和接收端之间通路的一种形象比喻,对于无线电波而言,它从发送端传送到接收端,其间并没有一个有形的连接,它的传播路径也有可能不只一条,因此无线信道,通常是指空气,又称为自由空间,传输的信号是无线电磁波。
1.2 信道的衰减特性
无论是电信号、还是光信号、还是无线电磁波信号,通过物理传输信道时候,其幅度会随着传输的距离的增加而衰减。
有线信道的衰减或损耗:
有线信道只有路径衰减,不存在多径衰减与地形阴影衰减。
无线信道的衰减或损耗:
在无线通信领域,衰落是指由于信道的变化导致接收信号的幅度发生随机变化的现象,即信号衰落。
路径损耗,或称传播损耗,指信号在空间传播所产生的损耗,是由发射功率的辐射扩散及信道的传播特性造成的
多径衰落:是指在微波信号的传播过程中,由于受地面或水面反射和大气折射的影响,会产生多个经过不同路径到达接收机的信号,通过矢量叠加后合成时变信号.多径衰落可分为平衰落和频率选择性衰落
阴影衰落: 移动通信中,由障碍物阻挡造成的阴影效应,接受信号强度下降,但该场强中值随地理改变缓慢变化,又称慢衰落。
1.3 信道频率特性与带宽
是指传输信道,对不同频率的信号的衰减特性。
(1)有线信道:
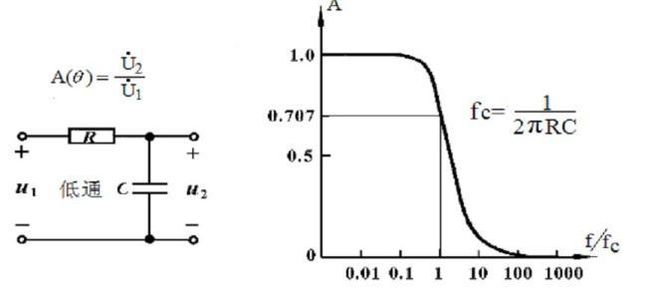
任何有线信道,都相当于一个低通滤波器,只能允许小于一定频率的信号通过,而这个频率,就是信道的截止频率。
由于有线信道,都允许直流信号的通过,信道的带宽,也是截止频率。
截止频率:当保持输入信号的幅度不变,改变频率使输出信号降至最大值的0.707倍,即用频响特性来表述即为-3dB点处即为截止频率,它是用来说明频率特性指标的一个特殊频率
截止频率或信道带宽表明:有线信道并不能传输所有频率的电信号,因此有限信道的带宽是有限的!
(2)无线信道:
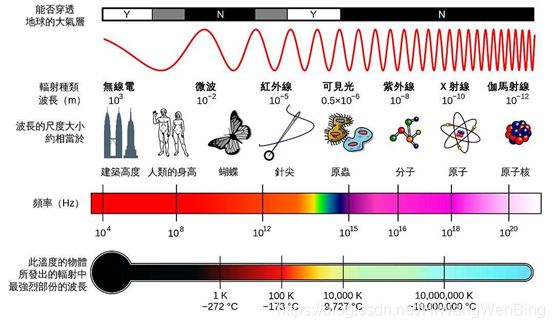
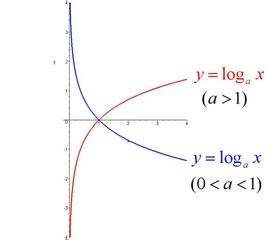
无线信道传输的是电磁波,其频率是一个连续的电磁波谱:
可以看出,理论上讲,无线信道的带宽是无限的,可以传输任何频率的电磁波!
注意:
这里的带宽,是信道的带宽,是从直流分量0频率到信道的最高频率、截止频率,而不是人为定义的一段电磁波谱。
第2章 数字通信与比特率、波特率
数字通信已经成为现代通信的主流,而数字信号通过信道进行传输一个个代表0或1的电信号,能够完整代表0或1的电信号,称为符号或波。表示0和1的电信号的符号有各种方法:
详见:《图解通信原理与案例分析-2:如何用电信号来表示和传输0和1,远远比我们想象的要复杂得多》
https://blog.csdn.net/HiWangWenBing/article/details/107897420
2.1. 代表二进制的“电”符号symbol
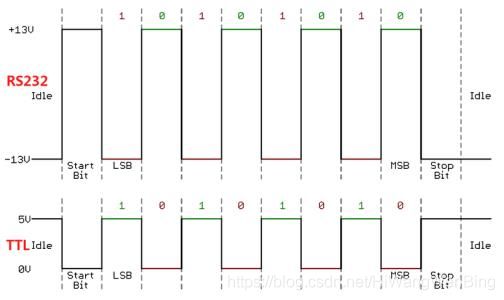
(1)用低电平表示0,1电平表示0, 在一个时钟周期内的高电平或低电平信号,就是一个符号。
(2)用正电平表示0,或负电平表示1. 在一个时钟周期内的负或正电平信号,就是一个符号。
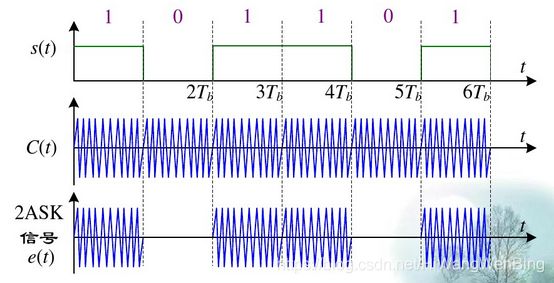
(3)二进制幅度2-ASK
n个幅度为A的载波信号整体,就是一个符号,代表0或1.
N= 1时,为最大符号率。
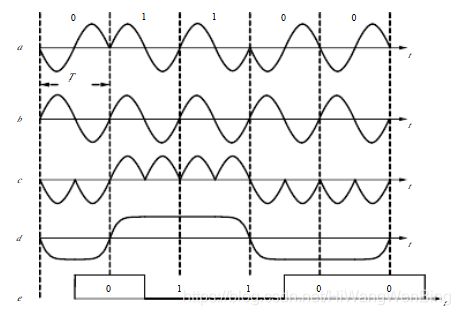
(4)2-PSK
N个完整的相位为 0°的电磁波信号表示0. N=1或2或。。。N的大小取决于传输的二进制的速率。
N个完整的相位为180°的电磁波信号表示1. N=1或2或。。。N的大小取决于传输的二进制的速率。
N= 1时为最大符号率。
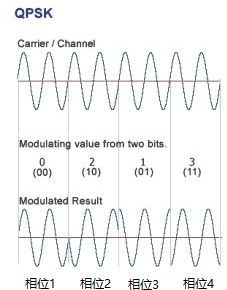
(5)Q-PSK
四个相位不同的波形,用来传递0或1. 每个波形就是一个符号。
N个完整载波周期的波形表示00,N=1或2或。。。N的大小取决于传输的二进制的速率,
N个完整载波周期的波形表示01,N=1或2或。。。N的大小取决于传输的二进制的速率。
N个完整载波周期的波形表示10,N=1或2或。。。N的大小取决于传输的二进制的速率。
N个完整载波周期的波形表示11,N=1或2或。。。N的大小取决于传输的二进制的速率。
N= 1时为最大符号率。
2.2 符号率、波特率、比特率
符号=波:传递二进制0和1的完整的电信号。
符号率=波特率:单位时间传递的完整的符号的个数。
比特率:单位时间传递的完整的二进制的个数。
如果每个符号代表1个比特,比特率= 符号率=波特率 ,比如单位时间能够传递1K个符号,就意味着能够传递1K个二进制比特。
如果每个符号代表2个比特,比特率/2= 符号率=波特率,比如单位时间能够传递1K个符号,就意味着能够传递2K个二进制比特。
如果每个符号代表3个比特,比特率/3= 符号率=波特率. 比如单位时间能够传递1K个符号,就意味着能够传递3K个二进制比特。
2.3. 最大符号率、 最大符波特率、 最大符比特率
由于信道是有最大带宽的,即有截止频率的。
因此,无论通过电平信号传递0和1,还是通过一定频率的正弦波/余弦波信号传递0或1,只要电信号,在信道中进行传输,就意味着,单位时间传递的符号或波的个数是受限的,也就是传递的二进制比特是受限的!
(1)携带二进制比特的符号是特定频率的正弦波
如下的二进制幅度2-ASK为例:
N个完整的载波正弦波表示0或1.
当N1=1是,表示一个完整的载波表示0或1,此时得到传输比特的最大上限。
如果传送的比特率再继续增大,那么在单个二进制比特周期内,只能传递不完整的载波信号,这样就会导致传输出错。
因此,在这种情况下,载波信号(符号)就是信道的带宽,单位时间传递的完整波形的个数,就是传递的二进制比特的上限。
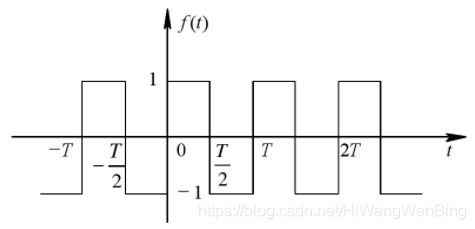
(2)携带二进制比特的符号的方波信号
此时方波信号周期,就是二进制比特的周期,方波信号的频率,就是二进制比特的速率。
如果方波信号的频率无限大,那么传递的二进制比特的速率就无限大。
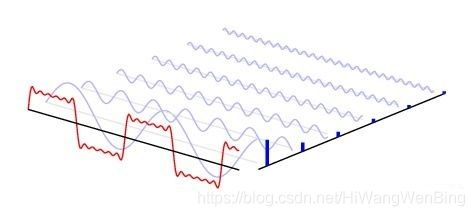
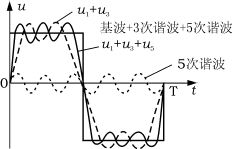
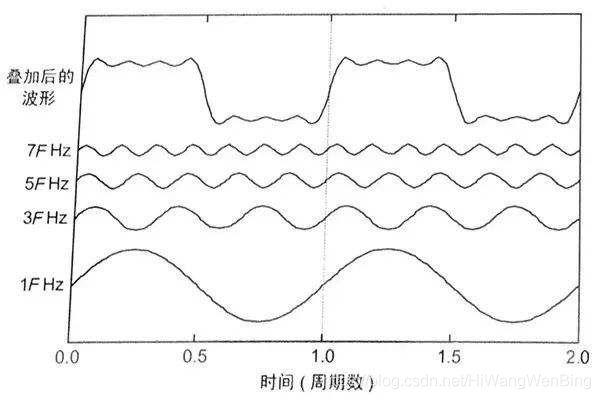
然而,根据傅里叶变换,方波信号实际上是由无限个具有谐波关系的正弦波信号叠加而成的,且基波的频率与方波的频率是相同的,因此,如果传播方波信号的信道是有截止正弦波频率的,那就意味着,方波符号的波特率也是受限制的,不能超过信道的截止频率。
![]()
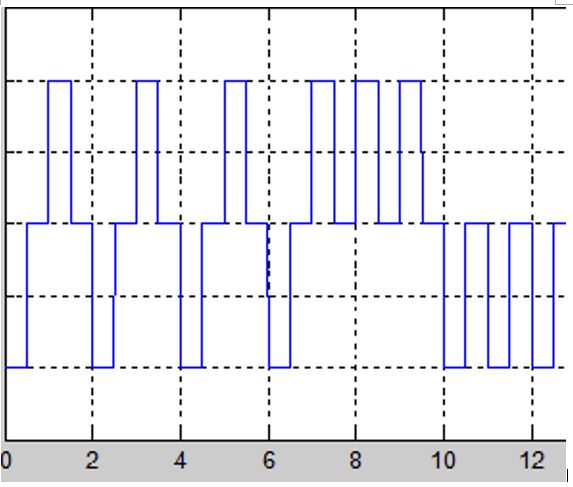
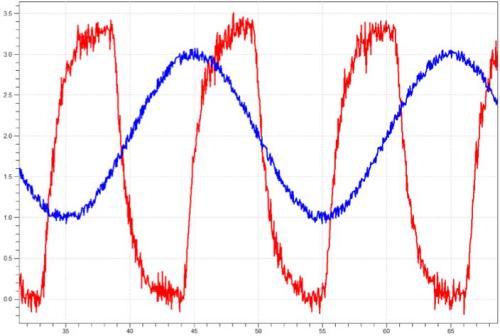
从上图可以看出,方波信号的周期与基波分量的周期是一致的,只是波形不同而已,通过基本分量,基本上可以还原方波信号!
当弱信道的截止频率,低于基波分量的频率,也就是信道把基波分量也过滤掉了,那么就很难还原方波信号了,也就是说,方波信号同构该信道,就会变形!
实际上,方波信号包含了高电平与低电平信号,相当于一个方波信号同时携带了0和1的两个符号,且不能分离,在这种情况系下,相当于二进制的符号率是方波信号的符号率的2倍。
当然,这种方式传递二进制是没有意义的,因为同时携带0和1,且0和1无法分离,对于接收端而言,无法区分0或1,但至少表明了一点,符号率可以做到是带宽的两倍!!!
那么如何解决词问题呢?
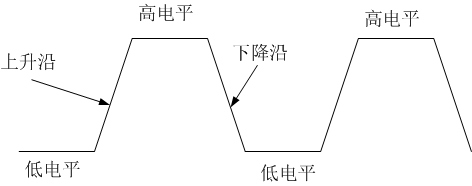
- 通过方波信号的上升沿与下降沿传递0或1信号
这样的话,这个方波信号/符号,就只能携带一个0或一个1。在这种情况下,方波信号的符号是带宽的1倍。
也就是说,在带宽确定的情况下,如果通过方波信号传递信息,是要牺牲二进制的比特率的。
当然,通过方波信号传递二进制也是能带来好处的:就是在传递数据的同时,也可以传递了时钟信号。
广泛应用在以太网中的曼切斯特编码,就是利用这个特性:牺牲二进制比特符号传输率,获得信号传输的时钟。
- 分离方波信号中的符号0和1,这就需要用矩形脉冲信号!
(3)携带二进制信息的双极性矩形脉冲信号
规定映射:0 -》 1, 1=》 -1;
双极性矩形脉冲信号的周期,就是二进制比特的周期!
双极性脉冲信号是指信道传输中常用的一种码形,它由一个正的振幅表示其一种状态,而由负的振幅表示其另一状态的数字信号。
矩形脉冲信号又称为为“门”信号、冲击脉冲信号等,它们相关,但由不完全一样。通过他们频谱的演变,可以看出脉冲信号与带宽的定性关系:
- 周期无穷小的冲激信号及其傅里叶变换分析
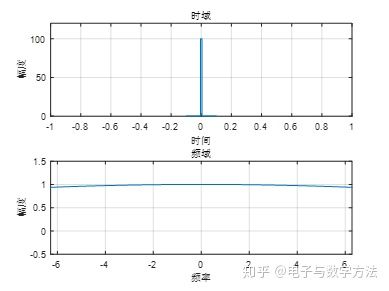
冲激信号信号的周期T无限接近于0,其理论频谱和带宽 B都 无限大。
冲激的频谱是一条直线,幅值为常数1,频率范围为无穷,即包好所有的频率成分,且每个频率分量的权重都是接近相等的。
因此,传输冲激信号的带宽必须是无穷的!
- 门信号及其傅里叶变换分析
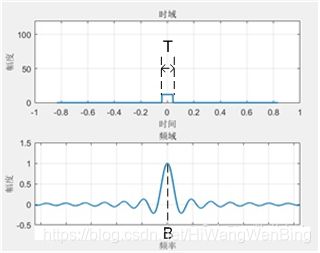
冲激信号的时间宽度趋于零,假设门信号的时间宽度为T,则我们可以推测门信号的频谱包含了许多成分,但不至于像冲激函数的频谱,包含所有的频率分量。门信号的频谱符合sinc函数的分布规律:
定性的来看,
门信号的持续时间越短,越接近冲激信号,内涵的每个频率分量的权重越接近相同。
门信号的持续时间T越长,即频率F越小,其频谱特性越接近sinc,内涵的每个频率分量的权重越符合上图的sinc函数的规律,高频分量的权重越小, 且基波频率B的值就越小。
门信号的持续时间T越短,即频率F越大,其频谱特性越接近冲激信号,内涵的每个频率分量的权重越符合上图的冲激信号函数的规律,高频分量的权重越大, 且基波频率B的值就越大。
在上图中,门信号频率f(F=1/T)与其频谱中的基波信号的频率B是一种线性关系:F=2B.
这个结论非常重要!这是奈奎斯特(Nyquist)准则的背后原因!
上述是从定性的角度理解信道带宽与最大传递的二进制之间的定性关系。
有没有一种方法,定量研究信道的带宽与传递的二进制比特率的关系呢?到底是什么数学关系呢?以及其别后的原理是什么呢?
这就涉及到奈奎斯特定理和香农定理。
第3章 奈奎斯特(Nyquist)准则
(1)什么是奈奎斯特(Nyquist)第一准则
奈奎斯特定理给出了理想的无噪声信道,信息传送速率的上限(比特每秒)和带宽的关系。
奈奎斯特定理可以解释现代各种通信信道由于带宽不同,所支持的信道最大吞吐量的不同。
1924年,奈奎斯特(Nyquist)就推导出在理想低通信道下的最高码元传输速率的公式:
Bmax = 2W(band)
其中W是理想低通信道的带宽,单位为赫兹;
Baud是波特,即码元传输速率的单位,1波特为每秒传送1个码元。
Bmax为最高波特率,是带宽的2倍!
当信道带宽为B时,发送的最大符号速率是2B,超过2B,接收方就会产生码间干扰,不能恢复出你原来发送的信息。
这就是奈奎斯特(Nyquist)第一准则。
(2)这里可能会有一个疑问:既然信道都是无噪声了,那为什么不是发送方发多快,接收方就能收多快呢?
这个问题答案是:实际信道是有带宽的,信道是一个低通滤波器,能够滤除高频信号,即阻止高频信号的通过,高频信号是无法通过信道的!
(3)第二个可能的疑问是:为什么是2倍的关系?
只所以最大波特率与带宽是2倍关系,主要原因是承载二进制比特信号“门”信号,而不是“方波”信号。
如果承载二进制比特信号是方波信号,其周期为T, 半周期为T/2,最大波特率与带宽是1倍关系。
如果承载二进制比特信号是门信号,其周期为T, 最大波特率F=1/T, 其与带宽B是2倍关系。即F<=2B.
因此,如果发送的波特率大于2B, 即每个符号的发送时间小于T, 其内含的基波分量的频率就会增加,大于原先的2B,如果信道带宽不变,导致基波信号无法通过该低通滤波器信道。
(4)波特率与比特率的关系
需要注意的是:奈氏准则并没有对二进制比特的传输速率(b/s)给出限制。
要提高信息的二进制比特传输速率,就可以使每一个传输的码元或信号波能够代表更多的比特的信息。这这个过程称为编码与调制。
如2-ASK: 每个符号传递1个比特
如2-PSK: 每个符号传递1个比特
如Q-PSK: 每个符号传递2个比特
如8-PSK: 每个符号传递3个比特
如16-QAM: 每个符号传递4个比特
如32-QAM: 每个符号传递5个比特
如64-QAM: 每个符号传递6个比特
如128-QAM:每个符号传递7个比特
如256-QAM:每个符号传递8个比特
如N-QAM:每个符号传递n个比特
波特率与比特率的关系为:
(5)奈奎斯特(Nyquist)准则比特率的表达式
如果N=2, 比特率=2 * 带宽W * 1 = 2 * 带宽W
如果N=4, 比特率=2 * 带宽W * 2 = 4 * 带宽W
如果N=8, 比特率=2 * 带宽W * 3 = 6 * 带宽W
如果N=16, 比特率=2 * 带宽W * 4 = 8 * 带宽W
如果N=32, 比特率=2 * 带宽W * 5= 10 * 带宽W
如果N=64, 比特率=2 * 带宽W * 6= 12* 带宽W
如果N=128, 比特率=2 * 带宽W * 7= 14* 带宽W
如果N=256, 比特率=2 * 带宽W * 8= 16* 带宽W
也就说,在信道带宽一定的情况,最大的波特率是固定的,即2倍的带宽。
但可以通过特定的编码或调制技术,来提升二进制数据的比特率!!!
第4章 香农定理
奈奎斯特(Nyquist)准则在理论上,在数学解决了一个重要的问题:
就是理想的无噪声的信道上,能够传送的最大的波特率(或码元率或符号率)与信道带宽之间的关系。
然而,理想是丰满的,现实是残酷的,显示的信道,往往都是有噪声的,根本不存在所谓的理想信道。
那么噪声的信道中,最大的波特率(或码元率或符号率)与信道带宽之间的关系又是什么关系呢?
在回答这个问题之前,先要定义和量化噪声,只有先量化了噪声,才能确定噪声对最终传输的二进制比特率的影响。
4.1 噪声的定义
从生理学观点来看,凡是干扰人们休息、学习和工作以及人们所要听的声音产生干扰的声音,即不需要的声音,统称为噪声。
从电通信的角度来看,凡是干扰正常电信号的其他所有电信号,统称为噪声。
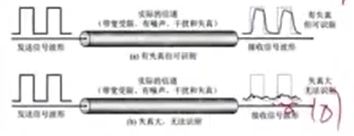
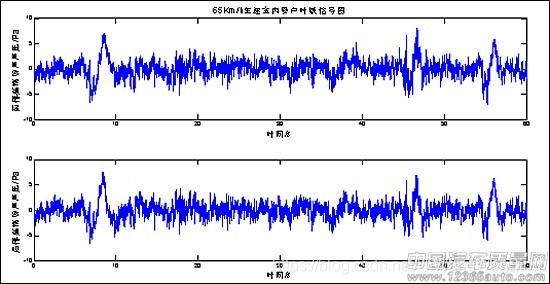
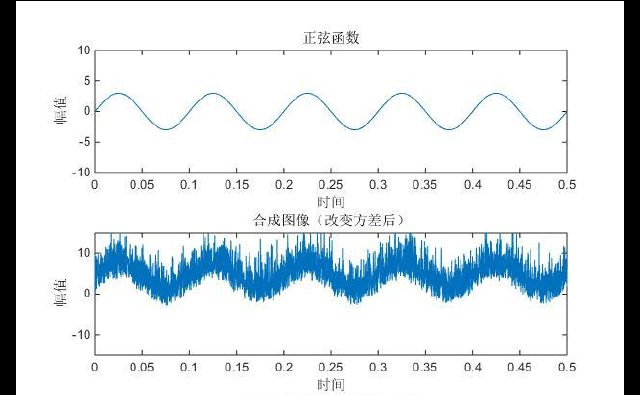
在上图中,信号的毛刺就是噪声造成的,这些噪声对信号是乎没有造成多大的影响。
在下图中,信号的毛刺就是噪声造成的,这些噪声对信号就造成了很大的影响。
4.2 信噪比定义
从上图可以看出,对于造成对有用信号的影响,噪声信号电平的绝对值是乎意义不大,而采用相对值可以反映噪声对信号的影响程度。
在通信中,采用信噪比来定义噪声对信号的影响程度。
信噪比,英文名称叫做SNR或S/N(SIGNAL-NOISE RATIO),又称为讯噪比。是指一个电子设备或者电子系统中信号与噪声的比值。
这里面的信号指的是来自设备外部需要通过这台设备进行处理的电子信号,
噪声是指经过该设备后产生的原信号中并不存在的无规则的额外信号(或信息),并且该种信号并不随原信号的变化而变化。
信噪比的计量单位是dB,其计算方法是10lg(Ps/Pn),其中Ps和Pn分别代表信号和噪声的有效功率,也可以换算成电压幅值的比率关系:20Lg(Vs/Vn),Vs和Vn分别代表信号和噪声电压的“有效值”。因此,信噪比应该越高越好。
SNR = 2*10lg(Ps/Pn) = 20lg(S/N)
需要说明的是:
(1)信噪比并非简单的线性比,而是先线性比,然后再取对数。
之所以,不是采用简单的线性比值,主要是因为线性比值的数字太大,表达起来不方便。在通信系统中,噪声的能量往往很小,因此Ps/Pn通常都比较大=10^6.
(2)信噪比 的单位是dB。
如果是简单的线性比值,是不因该有单位的,而是一个比例值,因为比值后再去对数,于是就有了单位dB
Ps/Pn = 10^0, SNR = 0 = 0dB
Ps/Pn = 10^1, SNR = 2*10 = 20dB
Ps/Pn = 10^2, SNR = 2*20 = 40dB
Ps/Pn = 10^3, SNR = 2*30 = 60dB
Ps/Pn = 10^4, SNR = 2*40 = 80dB
Ps/Pn = 10^5, SNR = 2*50 =100dB
Ps/Pn = 10^6, SNR = 2*60 =120dB
Ps/Pn = 10^7, SNR = 2*70 = 140dB
Ps/Pn = 10^8, SNR = 2*80 =160dB
Ps/Pn = 10^9, SNR = 2*90 =180dB
Ps/Pn = 10^10, SNR = 2*100=200dB
4.3 香农定理
(1)香农定理
香农定理证明:在被高斯白噪声干扰的信道中,传送的最大信息速率C由下述公式确定:
C=W*log₂(1+S/N) (bit/s)
C是数据速率的极限值,单位bit/s;
注意的是:这里的C不是波特率,而是比特率,已经包含了各种编码的效率等因素后的综合结果。
因此,香农定义预测的是,采用各种技术手段,所能够达到的最高传输速率。
log:2为底的对数
W为信道带宽,单位Hz;
S是信号功率(瓦),
N是噪声功率(瓦)。
香农公式中的S/N是为信号与噪声的功率之比,为无量纲单位。如:S/N=1000(即,信号功率是噪声功率的1000倍)
SNR(信噪比,单位为dB)=10 lg(S/N), 则
S/N=10^(SNR/10),如果SNR=20, S/N=10^(20/10)= 10^2 = 100。
通信信道的信道容量或香农限制是指在指定的噪音标准下,信道理论上的最大传输率。
可以用香农公式来计算电话线的数据传输速率。
通常音频电话连接支持的带宽W=3kHz,而一般链路典型的信噪比是30dB,即S/N=1000,
因此有C=3KHz × log2(1+1000),近似等于30kbps,
假如噪声值给定,那么似乎通过增加信号强度或带宽就能提高数据率;
但事实并非看起来这边简单。主要原因是信号带宽W与S/N并非完全独立的,而是是相关的。
(2) 通过提升信噪比提升数据传输比特率
理想情况下
但不能无限制的增加信号的强度来提升数据比特率,因为,如果信号强度增加了,则系统硬件的非线性程度也会提高,这就导致噪声的增加,在增加信号强度的过程中,噪声的强度也在增加。
因此,信号强度的提升,功率放大器的线性区间。
假设信噪比S/N=10^4, 带宽为W, 则最大的数据传输率C= W * Log2(1+10^4) ~= 13W, 也就是带宽的13倍。
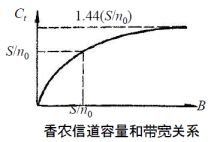
(3) 通过提升带宽提升数据比特率
不能无限制的增加信道的带宽来提升数据比特率,带宽越宽,系统容纳的噪声也就越多,因此随着B的增加,S/N反而降低了。
第5章 香农定理与奈奎斯特(Nyquist)准则的关系
奈奎斯特(Nyquist)准则比特率的表达式
C= 2* W*log₂ N(bit/s) = W * log₂ N^2(bit/s)
N是二进制编码代表的二进制的种类, N=2^1, 2^2, 2^3, .....2^8, 2^9, 2^10
N^2 = 2^2, 2^4, 2^6,..... 2^20.....
结论:在带宽一定的情况下,可以通过提升编码的效率,提升传送的比特数。
香农定理:
C = W * log₂(1+S/N) (bit/s)
S/N是信噪比。
S/N=10^1, 10^2, 10^3, 10^4.....
结论:在带宽一定的情况下,可以通过提升编码的效率,提升传送的比特数。
于是乎得到一个神奇的结果:
log₂ N^2 ~= log₂(1+S/N)
右边是有噪声信道, 右边是无噪声的信道。
这就意味着,链路的信噪比与符号的编码率之间有着一定的关系!
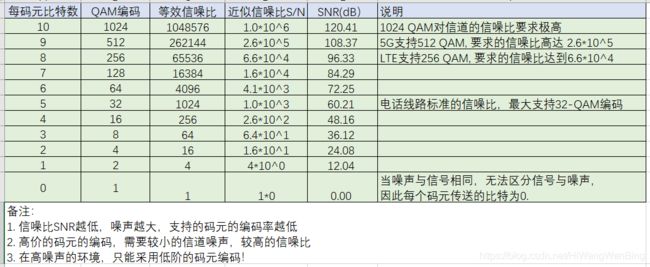
信噪比越大,支持的符号的编码的阶数越大,信噪比越小,噪声越大,支持的符号的编码的阶数越小。
下表展现了在带宽一定的情况下,信噪比与码元编码率的关系:
国际电工委员会对信噪比的最低要求是:
前置放大器大于等于63dB,
合并式放大器大于等于63dB。
后级放大器大于等于86dB,
合并式放大器信噪比的最佳值应大于90dB,
CD机的信噪比可达90dB以上,
高档CD的更可达110dB以上。
参考:
冲激信号、门信号、方波、矩形波的傅里叶变换总结: https://zhuanlan.zhihu.com/p/111522114
深入理解奈奎斯特第一准则与码间串扰: https://blog.csdn.net/weixin_44586473/article/details/104372110
奈奎斯特采样定理:https://haokan.baidu.com/v?vid=18289428643977245185&pd=bjh&fr=bjhauthor&type=video