Python音频信号处理 2.使用谱减法去除音频底噪

使用谱减法去除音频底噪

上一篇文章我主要分享了短时傅立叶变换及其逆变换在python中的实现，有兴趣的可以阅读一下该篇文章，地址如下：
Python音频信号处理 1.短时傅里叶变换及其逆变换

那么在本篇文章中，我们将利用短时傅立叶变换及其逆变换来实现谱减法。

Part 1 ：谱减法

谱减法的核心思路非常简单，顾名思义，谱减法是一种频域上的信号处理方法，其基本思路就是提取出信号本身的频谱以及噪音的频谱，通过两者之差获取降噪后信号的频谱，最后利用傅立叶变换逆变换重构初始信号。

Part 2 ：使用谱减法降低或消除信号的底噪

要使用谱减法来进行信号处理，显然我们首先需要计算出信号的频谱以及噪音的频谱。这里我们继续使用上篇文章所介绍的短时傅立叶变换及其逆变换的实现，Python代码如下：

# 短时傅立叶变换
def TFCT(trame, Fe, Nfft,fenetre,Nwin,Nhop):
  L = round((len(trame) - len(fenetre))/Nhop)+1
  M = Nfft
  xmat = np.zeros((M,L))
  print('xmat',xmat.shape)
  print(Nwin+Nhop)
  for j in range(L):
    xmat[:,j] = np.fft.fft(trame[j*Nhop:Nwin+Nhop*j]*window,Nfft)  
  x_temporel = np.linspace(0,(1/Fe)*len(trame),len(trame))
  x_frequentiel = np.linspace(0, Fe,Nfft)
  
  return xmat,x_temporel,x_frequentiel

# 短时傅立叶变换逆变换
def ITFD(xmat,Fe,Nfft,Nwin,Nhop):
  window = np.hamming(Nwin)
  Te = 1/Fe
  yvect = np.zeros(Nfft + (xmat.shape[1]-1)*Nhop)
  t_vecteur = np.arange(0,Te*len(yvect),Te)
  index = 0
  K = 0
  L = xmat.shape[1]
  yl = np.zeros((Nfft,L))
  for j in range(L):
    yl[:,j] = np.fft.ifft(xmat[:,j])
  for k in range(L):
    yvect[Nhop*k:Nfft+Nhop*k] += yl[:,k]
  for n in range(Nwin-1):
    K +=  window[n]
  K /= Nhop
  yvect /=K
  print(yvect.shape)
  return t_vecteur, yvect

有关于短时傅立叶变换及其逆变换的实现这里就不过多赘述，有兴趣的可以参考上一篇文章，其中详细解释了代码的构成。

首先我们先读取信号，并观察其在时域中的图像：

# 读取初始信号 mix.wav
Fe, mix = wavfile.read('mix.wav')
mix = mix/2**15
Te = 1 / Fe
xtemp = np.arange(0,Te*len(mix),Te)
plt.figure()
plt.plot(xtemp,mix)
plt.axis([0,1,-0.6,0.6])
plt.xlabel('t(s)')
plt.ylabel('amplitude(V)')
plt.title('representation of the original signal in time domain')
display(Audio(mix,rate=Fe))

Fe为原始信号的采样频率，mix为复信号值。
Te = 1/Fe = 6.25e-5

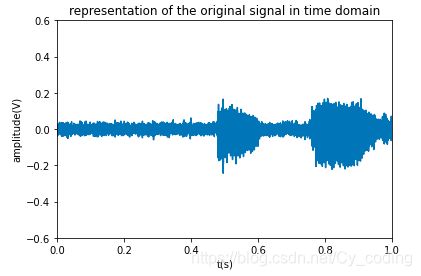
我们不难发现，0-0.4s，时域上只有底噪，因此我们可以利用这段时间来计算噪音的频谱。
这个例子中，我们选择频域的采样点个数Nfft=1024，窗函数的长度Nwin=1024，每次窗函数滑动的长度Nhop=512，计算该信号的短时傅立叶变换。

Nfft = 1024
Nwin = 1024
Nhop = 512
window = np.hamming(Nwin)
xmat_sound,tvect,fvect = TFCT(mix,Fe,Nfft,window,Nwin,Nhop)

xmat_sound就是我们保存短时傅立叶变换值的矩阵，该矩阵的每一行代表一个在0至采样频率范围内的频率，单位为Hz，每一列对应该段被窗函数截取的信号的FFT快速傅里叶变换值。
不难算出第一列代表的时域范围为0-Nwin*（1/Fe）= 0.064s
在该例中，我们就使用第一列的频谱，近似认为是底噪的频谱。（显然我们这里应该取尽可能多的纯噪音频谱，并使用他们幅值的平均值，这里为了简化仅使用第一个窗函数截取的信号部分作为噪声频谱。）

我们可以先使用imshow画出原始信号的光谱图，横轴为时间，纵轴为频率。

module_tf_xmat = abs(xmat_sound)
plt.figure()
xlim = int(module_tf_xmat.shape[0]/2)
ylim = int(module_tf_xmat.shape[1]/2)
plt.imshow(20*np.log10(module_tf_xmat[0:xlim,:]),extent=[0,Te*len(mix),0,Fe/2],aspect='auto')
plt.colorbar()
plt.xlabel('time(s)')
plt.ylabel('frequence(Hz)')
plt.title('spectrogram of the originql signal')

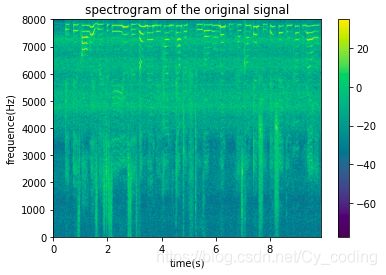
接下来我们使用谱减法，对信号频谱所有列减去第一列对应的噪音频谱，注意这里的全部减法都是针对幅值。

module_tf_xmat = abs(xmat_sound)
module_tf_bruit = module_tf_xmat[:,0]

module_reconstruit = np.zeros(module_tf_xmat.shape)
for n in range(module_tf_xmat.shape[1]):
  module_reconstruit[:,n] = module_tf_xmat[:,n] - module_tf_bruit
module_reconstruit[module_reconstruit<0] = 0

谱减法之后的光谱图如下所示：

最后我们使用短时傅立叶变换逆变换将获取的降噪后的幅值矩阵，使用原始的信号相位，重构降噪后的复信号。

# 将相位和降噪后的幅值重构复信号的频域分布
tf_reconstruit = np.zeros(module_tf_xmat.shape,dtype=complex)
for i in range(module_tf_xmat.shape[0]):
  for j in range(module_tf_xmat.shape[1]):
    tf_reconstruit[i,j] = module_reconstruit[i,j] * np.exp(angle_tf_xmat[i,j]*1j)
# 使用短时傅立叶变换逆变换重构时域内的信号
t,yvect = ITFD(tf_reconstruit,Fe,Nfft,Nwin,Nhop)

总结

在本例中，我们仅仅使用了短时傅立叶变换矩阵的第一列来计算噪声的频谱，实际是非常不准确的，因为此时所取的噪声长度仅为0.064s。即使是对于平稳的噪音，这段噪声的频谱仍然不能很好地代表噪音的真实频谱。在实际的信号处理过程中，较好的方式是取足够长度的噪音并计算其幅值的平均值，再使用这个噪音在各个频率幅值的平均值进行谱减法，可以更加有效地降低底噪。