概率论与数理统计学习笔记(2)——联合概率、条件概率与边缘概率
这篇文章主要是从一个直观的概念上讲解联合概率、条件概率与边缘概率。
主要是之前看了篇论文,用的SO-PMI算法,然后我就恶补了一下联合概率。
本篇博客采用的参考书是《程序员的数学2概率统计》。
目录
- 联合概率
- 边缘概率
- 条件概率
- 参考
这里先画一个程序员的数学上面的图,方便后续阐述,图没有书上那么好看,凑合一下:

红色部分代表住宅,白色部分代表工厂,蓝色部分代表农田。
左边是A县,中间是B县,右边是C县。
我发现国外的内容,关于概率这一块都是以面积等直观的东西来描述的,并非是纯粹的数字,我现在也在尝试从数字转换为面积这种思想转变,嗯,还是很难。
联合概率
联合概率,联合联合,指的就是几个东西联合起来的区域。联合概率一共有三种表达方式:
- P ( A B ) P(AB) P(AB)
- P ( A , B ) P(A,B) P(A,B)
- P ( A ∩ B ) P(A∩B) P(A∩B)
虽然市面上我看到的大多联合概率的表达都是第二种,但是其实第三种是我觉得最容易理解的东西,就是两个部分交起来。
比如上图,我们想知道A县住宅的面积,那么用联合概率表达为 P ( A , 住 宅 ) P(A, 住宅) P(A,住宅),也就是第一根竖着的线的左边的红色区块的面积。
联合概率中,如果两个事件是相互独立的,那么会有个结论:
P ( A , B ) = P ( A ) P ( B ) P(A,B)=P(A)P(B) P(A,B)=P(A)P(B)
我对这个公式的理解为:由于AB独立,那么AB是互不影响的,那么我AB同时发生的概率,就等于说是A发生的概率与B发生的概率之乘。
这里用另外一个不是书上的栗子说明(因为书上栗子我没看懂),就我连续丢一枚硬币两次,那么第一次的结果肯定是不会影响到第二次的结果对吧,我们观察下表:
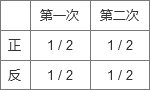
假设我们要测第一次和第二次都为正面的概率,即 P ( 第 一 次 = 正 , 第 二 次 = 正 ) P(第一次=正,第二次=正) P(第一次=正,第二次=正),我们会很自然而然的用 P ( 第 一 次 = 正 ) ∗ P ( 第 二 次 = 正 ) = 1 4 P(第一次=正)*P(第二次=正)=\frac{1}{4} P(第一次=正)∗P(第二次=正)=41,为什么,就是我们知道这是独立的,互不干扰,所以就直接相乘。(当然我感觉这有点违背推理过程了,因为是先知道的结果,再反推的过程,但是最重要的是理解何为独立)
所以给大家提个醒,如果你去买彩票,就别每次心理安慰买同一个号了,反正中奖概率也不会提高,毕竟都是独立事件,对吧。
这里继续回到之前说的土地面积的栗子,我们会得到一个结论:
P ( 住 宅 ) = P ( A , 住 宅 ) + P ( B , 住 宅 ) + P ( C , 住 宅 ) P(住宅)=P(A,住宅)+P(B,住宅)+P(C,住宅) P(住宅)=P(A,住宅)+P(B,住宅)+P(C,住宅)
P ( 工 厂 ) = P ( A , 工 厂 ) + P ( B , 工 厂 ) + P ( C , 工 厂 ) P(工厂)=P(A,工厂)+P(B,工厂)+P(C,工厂) P(工厂)=P(A,工厂)+P(B,工厂)+P(C,工厂)
P ( 农 田 ) = P ( A , 农 田 ) + P ( B , 农 田 ) + P ( C , 农 田 ) P(农田)=P(A,农田)+P(B,农田)+P(C,农田) P(农田)=P(A,农田)+P(B,农田)+P(C,农田)
P ( A ) = P ( A , 住 宅 ) + P ( A , 工 厂 ) + P ( A , 农 田 ) P(A)=P(A,住宅)+P(A,工厂)+P(A,农田) P(A)=P(A,住宅)+P(A,工厂)+P(A,农田)
P ( B ) = P ( B , 住 宅 ) + P ( B , 工 厂 ) + P ( B , 农 田 ) P(B)=P(B,住宅)+P(B,工厂)+P(B,农田) P(B)=P(B,住宅)+P(B,工厂)+P(B,农田)
P ( C ) = P ( C , 住 宅 ) + P ( C , 工 厂 ) + P ( C , 农 田 ) P(C)=P(C,住宅)+P(C,工厂)+P(C,农田) P(C)=P(C,住宅)+P(C,工厂)+P(C,农田)
上面三个公式,对应的就是从左向右看,下面三个公式,对应的就是从上往下看,那么这几个公式告诉了我们,当你确定某一个样本(比如县城或者用途)后,那么其余几项之和等于总的这一个样本的概率。
用公式表达(假设是两个随机变量)就是:
P ( X = a ) = ∑ b P ( X = a , Y = b ) P(X=a)=\sum_bP(X=a,Y=b) P(X=a)=b∑P(X=a,Y=b)
P ( X = b ) = ∑ a P ( X = a , Y = b ) P(X=b)=\sum_aP(X=a,Y=b) P(X=b)=a∑P(X=a,Y=b)
书上对于 ∑ b ( ⋅ ⋅ ⋅ ) \sum_b(···) ∑b(⋅⋅⋅)的解释是:穷举Y可取的值b后,由所有与这些值对应的(···)相加得到的和。
我个人觉得这个解释太繁琐了,用我个人的解释来说就是,我们把每个求和或者求积看作是一层循环,那么就是把a看作是常量(即固定X的值),循环每个Y(for y in Y),每轮都可以获得一个P(X, Y),把这些概率相加。
然后这个循环就可以引出我们下一个话题:边缘概率。
边缘概率
边缘概率指的就是,固定住某一个值,另外一个值变化的概率,即只关心一个变量的概率分布,而不再考虑另一个变量的影响。其实这也是个降维的过程,假设我们是两个随机变量,我们固定住某一个变量,那么是不是我们考虑的东西就是一维的东西了?
我用浙江大学《概率论与数理统计》第四版的例题一来给大家直观感受下边缘概率(主要是我抠脑壳想不出来)。题目如下:
一整数N等可能的在1,2,3,···,10十个数中取一个值,设D=D(N)是能整除N的正整数的个数,F=F(N)是能整除N的素数的个数(1不是素数),试写出D和F的联合分布率,并求边缘分布率。
样本空间,D以及F取值情况如下:
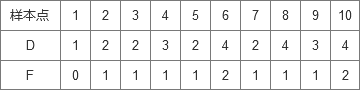
联合分布率与边缘分布率如下:
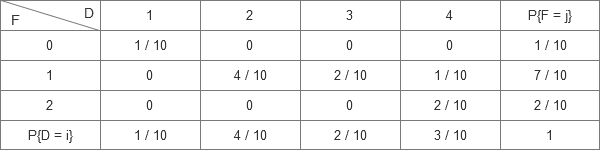
最下面那一行和最右边这一列就是边缘概率,中间的那一坨坨就是联合概率。
条件概率
最后我们再来谈谈条件概率。
条件概率就是指在某个条件下,另外一个的概率,用公式表达为 P ( A ∣ B ) P(A|B) P(A∣B),即在B的情况下,A发生的概率。
就比如上面的面积图, P ( 工 厂 ∣ A ) P(工厂|A) P(工厂∣A),代表的就是在A县的工厂的面积。
条件概率有个公式:
P ( 工 厂 ∣ A ) = P ( 工 厂 , A ) P ( A ) P(工厂|A)=\frac{P(工厂,A)}{P(A)} P(工厂∣A)=P(A)P(工厂,A)
这个公式后半部分的意思就是,A中工厂占A的面积(概率)是多少,即A中工厂的面积。还没搞懂的同学,不妨想一想,我们求某个事件A在某个范围 ω \omega ω内发生的概率,我们是不是直接求 A ω \frac{A}{\omega} ωA,这里也是一样的,就是上面的联合概率,在某个范围内发生的概率。
那么我们来总结下,联合概率针对的是某几个条件在某个范围中发生的情况,条件概率是在某个条件成立的情况下的某个事件的概率。而从公式和上面的面积图来看,联合概率就是几个框框的交集部分,而条件概率就是这个框框的交集占某个部分的面积。
那么如果是独立的情况,条件概率可以转换为如下的公式:
P ( A ∣ B ) = P ( A , B ) P ( B ) = P ( A ) P ( B ) P ( B ) = P ( A ) P(A|B)=\frac{P(A,B)}{P(B)}=\frac{P(A)P(B)}{P(B)}=P(A) P(A∣B)=P(B)P(A,B)=P(B)P(A)P(B)=P(A)
这个公式表达的意思也很直观,就是我们既然独立,那么我成立于否与你是否是我的条件有个毛的关系啊,即我就是我自己,我不欠你100块,那种感觉。
参考
[1]平冈和幸,堀玄.程序员的数学2概率统计[M].人民邮电出版社:北京,2015-8:29-55.
[2]盛骤,谢式千,潘承毅.概率论与数理统计(第四版)[M].高等教育出版社:北京,2009-8:64-65.