常数时间生成集合划分

常数时间生成集合划分

本文章是Shin-ichiro KAWANO and Shin-ichi NAKANO的论文 constant time generation of set partition的部分翻译，限于译者的水平,不保证准确，本文最后的插图也是来自此论文。

绪论

在实践中常常需要生成一个包含N个元素的K子集划分。其中每个子集都是非空子集，而且全集中每个元素都是相互可区分的，但是子集中的元素没有顺序观念，只是一个集合。因此我们给全集中每个元素生成一个标号，按任意顺序排列元素，然后从1标号到N。因此前述问题可以等价为1-N这些自然数分割为K个子集，下面要描述的算法就是这样一个渐进意义上的常数时间算法，来生成每一个的符合要求的划分。之所以说是常数时间，是因为每生成一个划分需要的时间一般为常数，但是由于有些划分需要回溯，所以是渐进意义上的常数时间。

记号及表示

一个包含N个不同元素的K划分定义为P(n,k)，而总的划分数目是S(n,k)。对于S(n,k)，我们有下面这个公式。

$$S(n,k)=S(n-1,k-1)+S(n-1,k)*k$$

我们可以这样解释这个公式，对于第n个元素，如果它单独为一个子集，则这样的划分数为S（n-1,k-1）,如果最后一个元素是跟其他元素在同一个集合中，可以先对剩下的n-1个元素生成k划分，然后在把当前元素插入到这k个集合的随便一个中，因此得到了上述结果。

把一个符合结果的划分按照每个子集中最小元素来排序，然后按照顺序给这些集合生成1-k标号，表示为\(B_1\)------\(B_k\)，可以看出1这个元素一定在中。

生成这些集合之后，我们在使用一个数组来表示第号元素所在的集合，即。因此对于n=6时，对于（1，2，4），（3，6），（5）这样的一个划分我们可以表示为位置数组

112132。而且，对于任意的n和k，位置数组之间都有一些限制条件。

1. 对于\(i=1,a_i=1\) ，恒成立
2. 对于\(i>1\)，\(a_i<MAX(a_1,\cdots,a_{i-1})+1 \)
3. \(k=MAX(a_1,\cdots ,a_n)\)

对于满足这些条件的数组，我们称之为K限制的生长序列。

操作及其定义

下面的操作都是作用在K限制的生长序列上的，不再另行说明。

回溯操作

对于任何一个K限制的生长序列，可以分为两种情况讨论。

第一种情况：当前序列为非递减序列时。即\(a_1\leq a_2 \leq \cdots \leq a_n\)。

对于这种情况，我们定义一个根序列，这个根序列会在后面一直用到-------11...123...k。

设\(a_j\)是从最右端向左数第一个与根序列不同的数，此时\(a_j=a_{j+1}\), 这个是由于当前序列为非递减序列。由于非递减，\(a_j <a_{j+1}\) ,而且当小于号成立的时候，不管 是变大了还是变小了，中间总是会有有一个数就不会出现，这个就违反了生长序列的定义。且\(a_{j-1}=a_j\)或者\(a_{j-1}=a_j -1\) ，此时 ，我们将\(a_j\)减少1。此时1，2，3这三个条件都成立，不违反K限制的生长序列的定义。

第二种情况：当前序列有一个或多个逆序对，即存在，使得\(a_j >a_{j+1}\)。

设b是从右往左数第一个满足\(a_b >a_{b+1}\)的位置，此时对于这个位置和其后继交换一下元素。交换之后，第一个条件和最后一个条件一定是满足的，而且第二个条件也是满足的。所以交换完成的序列还是K限制的生长序列。

我们把最后生成的序列定义为当前序列的父序列，即\(P(A)\),其中A为当前序列。从这里可以看出，每个不是根序列的当前序列都有一个唯一的父序列。

此外，我们可以证明任何一个包含N个元素的K划分所生成的位置数组可以通过前面的两个操作得到根序列：当位置数组中有逆序对时，可以通过第二种交换操作，最终得到一个没有逆序对的位置序列，其实可以当作冒泡排序，所以步骤是有限个的。当得到非递减序列之后，采取第一种操作。因为第二种操作消除逆序对，然后第一种操作将整个位置数组的和减1，并可能引发第二种操作。而一个集合的划分所得到的位置数组的最小和是跟序列的数组和，而且对于这个和只有根序列这种排列形式，所以最终会得到根序列。

 

生成操作

前面的回溯操作证明了任何一个非根序列都有一个唯一的父序列，而且每个符合条件的划分的位置数组都可以通过回溯操作回到根序列。但是我们的目的是为了生成所有的子序列，于是下文开始讨论如何从父序列生成子序列。

同样是分类讨论，从上面的回溯操作来得到父序列的响应特征。

第一种情况：子序列与父序列是通过第一种回溯操作联系起来的。

这时，假设减少的是第x个元素，由于操作前第x个元素等于第x+1个元素，第x-1个元素等于第x个元素或比第x个元素小1。因此操作完成之后父序列（x-1,x）可能成为逆序对，再次对是否有逆序对开始讨论。

1. 当前序列有且只有一个逆序对（x-1,x）

   此时如果存在y>=x且\(a_y = a_{y+1}\)，那么不可能从一个子序列回溯到父序列。因为第一个操作完成之后，对于下标大于x的位置数组元素是严格按照递增序排列的。因此如果存在这个y使得\(a_y=a_{y+1}\)，则不可能有可通过第一个回溯操作生成当前序列的子序列。

   如果不存在这个y，且\(a_x +1 =a_{x-1}\)，则可以直接将加上一个1，所得的序列仍然符合K限制的生长序列。如果\(a_x +1 =a_{x-1}\)这个条件不成立，则没有符合第一种回溯操作的子序列

2. 父序列没有逆序对

   从右向左找到第一个x，使得\(a_x =a_{x-1}\)。

   如果x不等于N，则此时直接将\(a_x\)加上1就得到了符合条件的子序列。

   如果x等于N，这时不存在可以通过第一个回溯操作生成当前序列的子序列。因为根据第一个操作的条件，子序列的最后一个元素一定是K，这时减法操作一定不会操作在这个元素上，所以加法操作作为逆操作也不会出现在这个元素上。所以此时不存在与第一种回溯操作对应的子序列。

第二种情况：父序列与子序列是通过第二种回溯操作联系起来的 。

因为子序列变为父序列时，是通过交换来消除最右边的一个逆序对的。所以由当前序列来得到子序列时，需要在当前序列中找到一个符合条件的增序对，并通过交换操作得到子序列。

但是在这里，条件是非常复杂的，下面首先通过分析子序列经过第二种回溯操作产生的父序列的性质来判断当前序列是否有第二种回溯操作下的子序列。

假设子序列为\(c_1 c_2 \cdots c_n\)，其中我们交换的是\(c_j ,c_{j+1}\)，因此对于大于j+1的那些元素是非递减序列，因为当前交换的是最右边的逆序对。交换完之后，可能对于大于等j的那些元素形成了新的非递减序列，甚至更长，也可能\(c_j ,c_{j+2}\)形成了新的逆序对，这些在下面来讨论。

1. 如果生成了新的逆序对

   设当前序列为\(p_1 p_2 \cdots p_n\)，假设\(p_b ,p_{b+1}\)是当前序列中最右边的一个逆序对。如果这个逆序对是子序列生成父序列的时候生成的新的逆序对，则原来\(c_{j+1}\)的变成了现在的，由于原来的\(c_{j+1},c_{j+2}\)是非逆序对，所以父序列中必须有\(p_{b-1} \leq p_{b+1}\)。如果不符合这个条件，则不可能通过交换这个逆序对前面的那一对数即\(p_{b-1} , p_b\)来得到子序列。如果符合这个条件，则可以通过交换这个\(p_{b-1},p_b\)来得到子序列。

2. 如果没有生成逆序对

   设当前序列为\(p_1 p_2 \cdots p_n\)，因此要交换相邻的一个增序对来抵消相应的回溯操作，而且这个顺序对的右边不能有逆序对，否则子序列中交换的不是最右端的逆序对，产生冲突。假设\(p_b,p_{b+1}\)是当前序列中最右边的逆序对，可以选择这个对右边的任何一对来进行交换从而生成子序列。但是这时还要考虑k限制的生长序列的第二个条件，即 \(a_i<MAX(a_1 \cdots a_{i-1}) +1\)。

3. 因此，如果交换的是\(p_i ,p_{i+1}\)，交换完之后的序列是\(p_{i+1} p_i\)。此时如果\(p_{i+1}\)是比当前序列的前(i-1)个数都大的时候，根据生长序列的第二个条件，有\(p_i\leq p_{i+1}+1\)。又因为这两个数交换之后是逆序对，即\(p_{i+1}>p_i\) 。因此\(p_i \neq p_{i+1}+1\)，此时可以描述为，增序对\(p_i ,p_{i+1}\)都比这两个元素之前的元素的值大，且\(p_i=p_{i+1}+1\)时没有子序列。其他情况下都有相应的子序列，即直接把这个增序对交换即可生成子序列。注意在这种情况下，同一个当前序列可生成多个子序列，也可能无法生成子序列。 

综合生成

通过上面讨论的结果，我们可以递归的从根序列下降，不停地生成子序列，直到不能生成为止。由于我们在生成子序列的过程中，第一种生成操作和第二种生成操作都会使用，且在生成过程中保持了k限制的生长序列的性质，所以生成的所有子序列都是一个集合的合理划分。又因为每个集合的合理划分都可以回溯到根节点，所以从根序列递归生成的所有序列就是所有的合理划分。而且，我们可以看出每生成一个子序列和每回溯到父序列所需要的时间都是线性有界的，而且每个节点最多遍历两次。所以，平摊下来的每子序列的生成时间为常量，这就是标题中常量时间的由来。其实，整个生成过程可以理解为一个多叉树的遍历，如下图所示。其中，虚线表示的为第一种方式的生成，实线表示的为第二种方式的生成。因为树的遍历方法有很多种，但是因为根节点要先遍历，因此只剩下了先序遍历和层序遍历这两种。

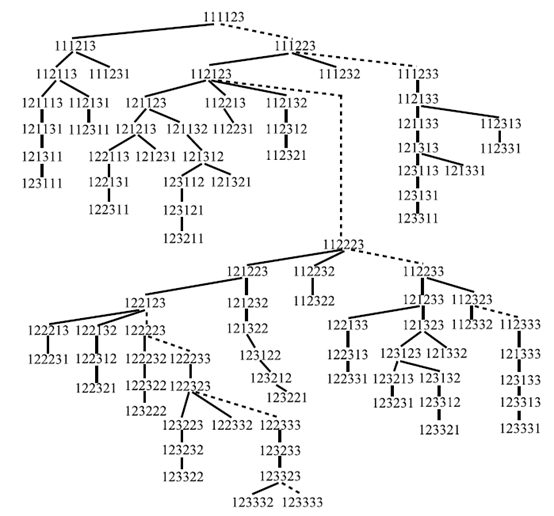
而先序遍历在多叉树中不怎么可行，不像二叉树中可以明确的分为左节点和右节点。所以考虑层序遍历，这时可以使用队列来进行遍历，但是由于可能于同一层中的节点数太多导致内存不够的情况出现。所以使用递归方法，每得到一个节点，就把当前节点可以生成的所有子节点入栈，然后选择一个子节点递归生成，如果节点没有子节点则出栈。这样可以缩小内存占用，但是递归的成本也是比较大的，值得注意。