机器学习—回归工程（案例：考试是否通过）

回归工程

一、线性回归

1.定义与问题引入

举个栗子

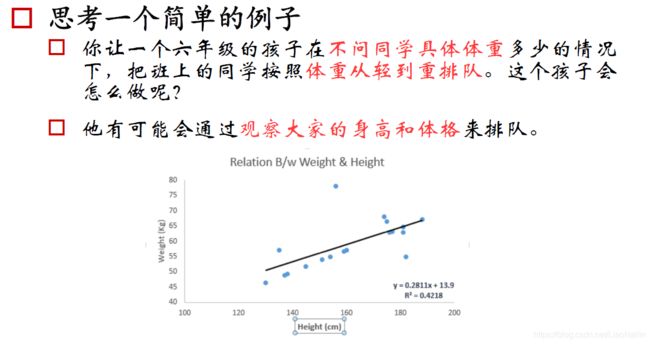
我们通过对大量的身高体重数据进放到一个直角坐标系中得到一个散点图（例如下图），干经过观察，我们发现。身高和体重关系趋近于一条线，用这样一条线可以大概的估计出一个身高对应的体重，或者一个体重对应的身高。那么问题来了，我们怎么样得到这样的一条直线呢？先让我们来了解一下损失函数

2.损失函数和梯度下降

假定我们用$y=1/2x$来拟合我们得身高体重的线性关系，那么我们发现是有偏差的。此时我们的$a=1/2（斜率）$此时发现，拟合的程度不够，明显我们需要的斜率（模型参数）小了，那么我们怎么确定那个斜率下我们的$y=ax+b$能最好的拟合我们的身高体重的散点图呢？

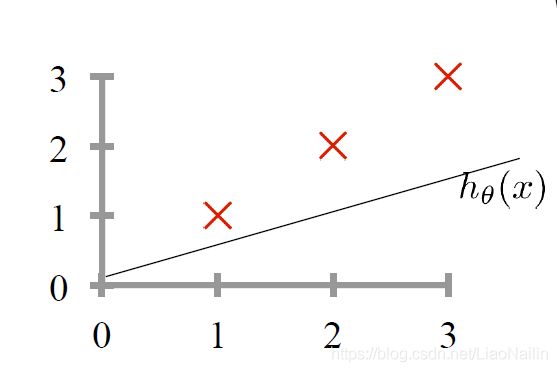
回顾一下初中的数学知识，点到直线的距离

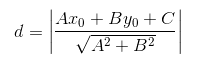
这个距离表示的是预测与实际的误差，常被称为损失值，把所有的点的损失值加起来，通过变化$y=ax+b$的参数a，记录出一个凸函数图像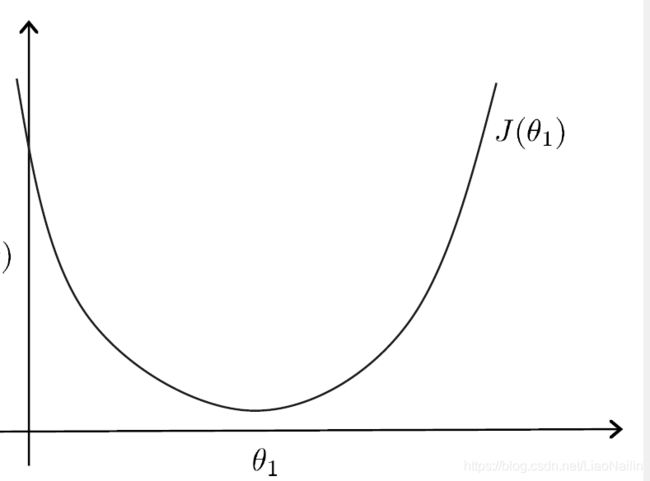
在该图的函数就被称为损失函数，顾名思义，损失函数我们为了求到一个局部最优的解，当然是取极小值，得出对应的$a(斜率)，b（截距）$，那么问题又来了，我们怎么样得到这个函数的最小值呢？
在回顾一下初中的数学知识，求导。
导数：在该函数某一点若导数大于零，则单调递增；若导数小于零，则单调递减；导数等于零为函数驻点，不一定为极值点。需代入驻点左右两边的数值求导数正负判断单调性。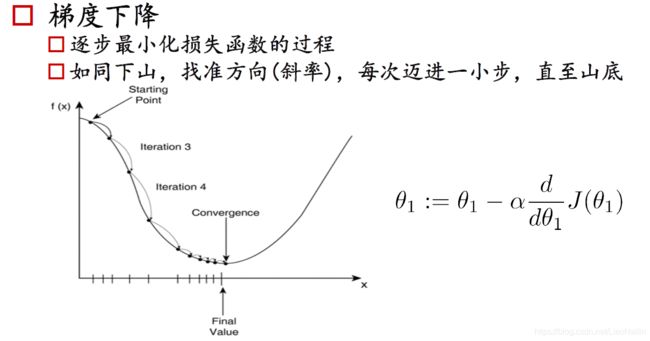
观察上图，先不要看公式，我们在y的最高处有一个Starting开始下山，在此进行求导，得到的一个导数值为负数，那我们为了求一个最小值，应该怎么做呢？是不是应该给$x$进行右移呢？然后我们在新的$x$放入函数求导发现还是小于零，那么重复以上操作，直到求导大于零，就可以得到一个趋近于最小值的点了。拿有同学又要问了，我一步向右走多远呢？要是我直接一脚跨过对面的山头怎么办？这时候就有了我们的梯度下降法。

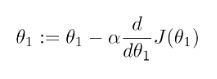
$\alpha$我们就是我们的步长（学习率），通过 $(-\alpha \ast \theta 的导)$当我们处于下坡时，该值得到的是一个负数，负负得正，此时我们的方向是向右，当我们超过最低点，到达对面上坡段时，$(-\alpha \ast \theta 的导)$得到一个正数$\theta -一个正数$他是不是右开始往坡底走了？

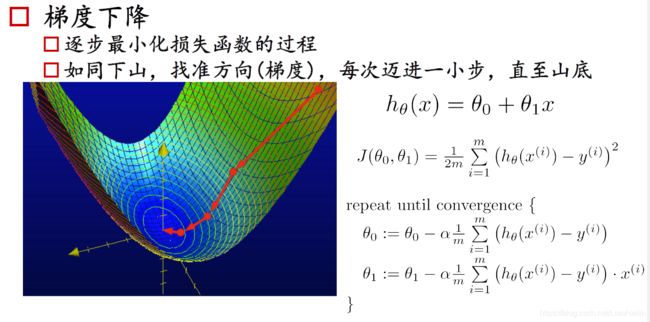
那么又有聪明的小朋友提问了，怎么选择合适的步长呢？ 通过思考我们发现，学习率大的计算次数少，但是不容易得到最优解，有时候太大了，就一直在上面跨来跨去，甚至是越来越高。学习率小的，计算的次数就会很多很多，下山的速度就非常的慢。此时这个值我们把它称为超参数，最开始我们是拟定这个值，通过观察和一系列的算法不断优化得到一个关于这个损失函数的最合适的学习率。

二、逻辑回归

1.定义与问题引入

敲黑板（来罗来罗）：逻辑回归跟线性回归有什么区别呢？逻辑回归用于处理分类问题，线性回归用于处理一个连续型的问题。

举个栗子

假设中考啦，分数是很多很多科，简单点，就语文数学吧，英语就让它一边去吧
我们通过这两科的成绩进行一个预测，预测该学生是否有高中读，笔者这里有一堆模拟的数据数据包括语文数学成绩，以及是否录取，这三项。
我们通过python的科学库对数据进行读取，然后规格化

# %load ../../standard_import.txt
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

from scipy.optimize import minimize

from sklearn.preprocessing import PolynomialFeatures

pd.set_option('display.notebook_repr_html', False)
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 150)
pd.set_option('display.max_seq_items', None)
 
#%config InlineBackend.figure_formats = {'pdf',}
%matplotlib inline

import seaborn as sns
sns.set_context('notebook')
sns.set_style('white')

def loaddata(file, delimeter):
    data = np.loadtxt(file, delimiter=delimeter)
    print('Dimensions: ',data.shape)
    print(data[1:6,:])
    return(data)

def plotData(data, label_x, label_y, label_pos, label_neg, axes=None):
    # 获得正负样本的下标(即哪些是正样本，哪些是负样本)
    neg = data[:,2] == 0
    pos = data[:,2] == 1
    
    if axes == None:
        axes = plt.gca()
    axes.scatter(data[pos][:,0], data[pos][:,1], marker='+', c='k', s=60, linewidth=2, label=label_pos)
    axes.scatter(data[neg][:,0], data[neg][:,1], c='y', s=60, label=label_neg)
    axes.set_xlabel(label_x)
    axes.set_ylabel(label_y)
    axes.legend(frameon= True, fancybox = True);

data = loaddata('data1.txt', ',')
X = np.c_[np.ones((data.shape[0],1)), data[:,0:2]]
y = np.c_[data[:,2]]

plotData(data, 'Exam 1 score', 'Exam 2 score', 'Pass', 'Fail')

然后绘制散点图，分别区分开正样本（录去）和负样本（不录取）得到这么个玩意

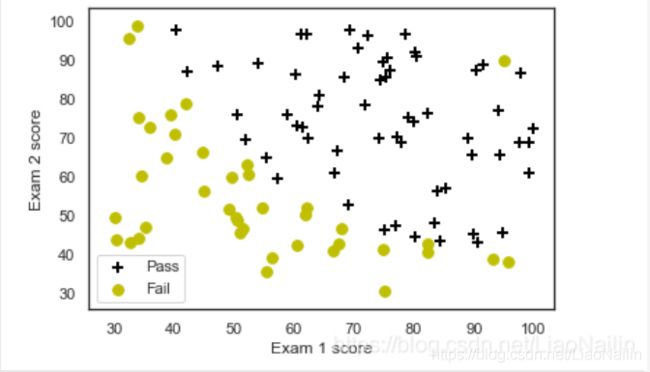
唉？怎么回事？在×中怎么会有一个⚪呢？

这种情况我们称为噪声、噪点也行。有可能是这家活考试作弊，然后分数是那么多但是被开除了不是。这里在后面我们还会涉及到数据清洗这样的一个操作（降噪）。这时候又有热心的同学问了，那机器怎么知道他的这个成绩是否能被录取呢？常用的算法有逻辑回归，k近邻算法等，此处我们通过逻辑回归进行分类

2.损失函数和梯度下降

损失函数又来啦，此时如果通过一个线性回归的方式来处理，好像有点牵强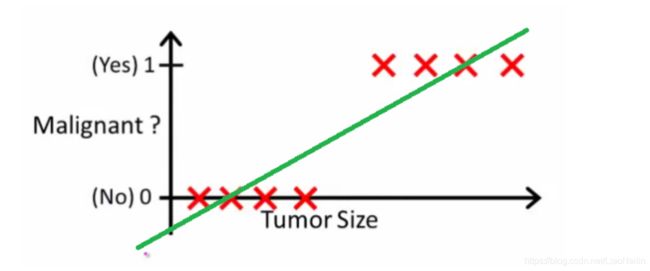

线的下方标识被fall了，上方表示pass。那就发现线性的损失函数不能很好的拟合这些分类问题了。怎么办呢
$sigmoid$函数
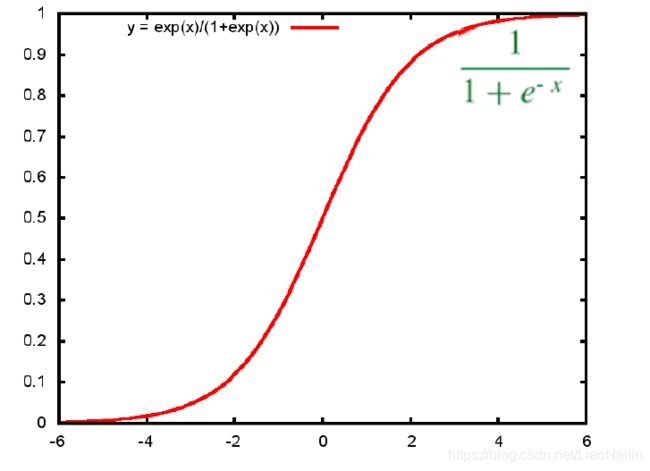
通过这个函数和线性回归函数的结合，我们可以吧问题变成一个01的问题。例如我们线性回归上的函数代入两科成绩得到80，80代入sigmoid函数中我们得到一个0-1的值这个值大于0.5则认为事情发生反之则反。然后再通过不断调整线性回归的参数得到一个损失函数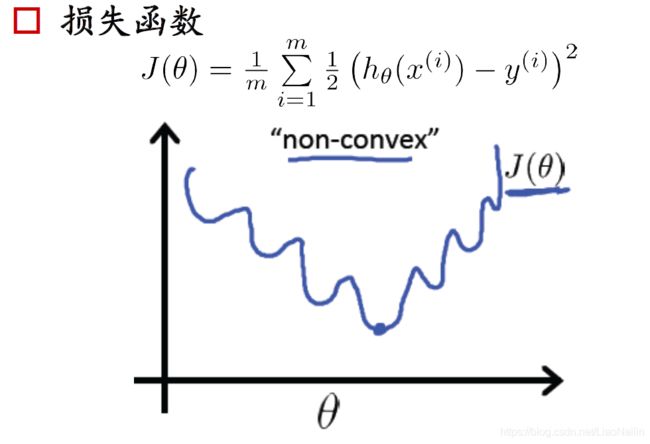
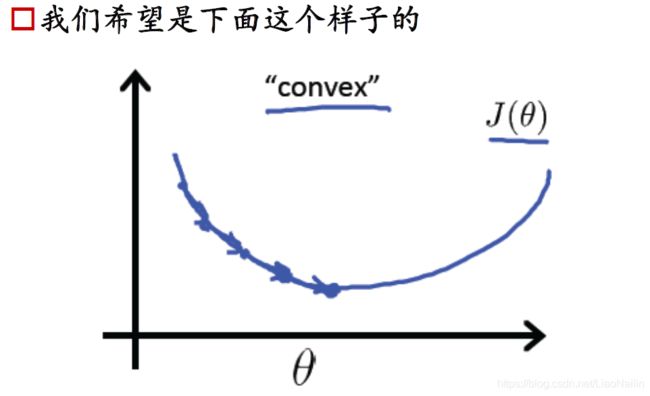
梯度下降又来啦可是在分类问题中，他的损失函数都是这种多个凸的函数，非常不容易求最小值，想象一个球调到这个山谷里很容易卡在半山，而得到一个局部最小值。那么

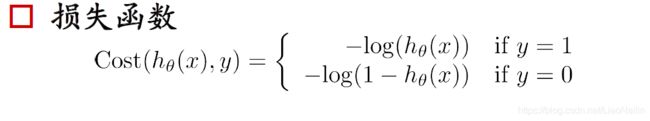
我们进行一个取对数操作

损失函数正则化：()=1∑=1[−()(ℎ(()))−(1−())(1−ℎ(()))]

#定义sigmoid函数
def sigmoid(z):
    return(1 / (1 + np.exp(-z)))
#定义损失函数
def costFunction(theta, X, y):
    m = y.size
    h = sigmoid(X.dot(theta))
    
    J = -1*(1/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))
               
    if np.isnan(J[0]):
        return(np.inf)
    return(J[0])

#求解梯度
def gradient(theta, X, y):
    m = y.size
    h = sigmoid(X.dot(theta.reshape(-1,1)))
    
    grad =(1/m)*X.T.dot(h-y)

    return(grad.flatten())
    
initial_theta = np.zeros(X.shape[1])
cost = costFunction(initial_theta, X, y)
grad = gradient(initial_theta, X, y)
print('Cost: \n', cost)
print('Grad: \n', grad)

# 这里偷懒了，直接调用scipy里面的最小化损失函数的minimize函数
res = minimize(costFunction, initial_theta, args=(X,y), method=None, jac=gradient, options={
     'maxiter':400})

那么我们通过损失函数有了这么一个比较合这个数据的参数模型，我们开始进行预测

#预测功能
def predict(theta, X, threshold=0.5):
    p = sigmoid(X.dot(theta.T)) >= threshold
    return(p.astype('int'))
    
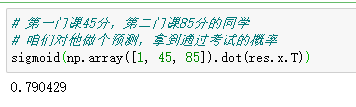
# 第一门课45分，第二门课85分的同学
# 咱们对他做个预测，拿到通过考试的概率
sigmoid(np.array([1, 45, 85]).dot(res.x.T))

得到这么一个结果，该同学通过考试的概率为0.79.。。。。。。

#绘图
plt.scatter(45, 85, s=60, c='r', marker='v', label='(45, 85)')
plotData(data, 'Exam 1 score', 'Exam 2 score', 'Pass', 'Failed')
x1_min, x1_max = X[:,1].min(), X[:,1].max(),
x2_min, x2_max = X[:,2].min(), X[:,2].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
h = sigmoid(np.c_[np.ones((xx1.ravel().shape[0],1)), xx1.ravel(), xx2.ravel()].dot(res.x))
h = h.reshape(xx1.shape)
plt.contour(xx1, xx2, h, [0.5], linewidths=1, colors='b');

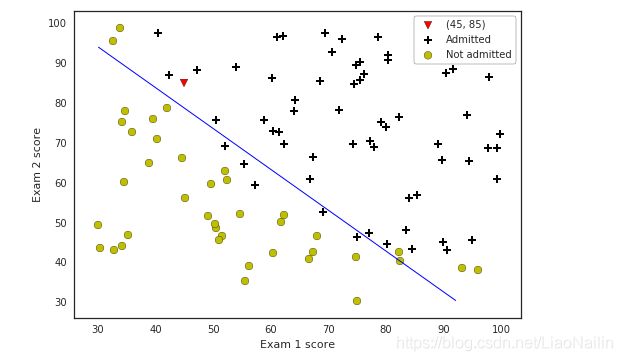
机器预测得出结果至此结束。
有同学又开始杠了，这个问题我两个成绩取平均值然后设置上下限不行啊？
嗯是的，针对这个问题有太多的解决方案。那么数据复杂化，多维度化呢？假如我们在区分贵族学校，在加入一些属性，例如家庭收入、居住地区房价、该家庭年教育支持 等多个数据来判断一个学生可以录取，他会不会来我这里读书呢？再次简单的使用平均，明显不妥吧，因为每一项的权重明显不同，家里有矿的有钱，但是爸妈不想读书，也不支持小孩读书呢？家里经济一般，但是很重视小孩的教育，每年在教育支出非常多的小孩呢，还有家庭住址离校距离等多个可能有影响的原因。

小结

其实这些功能都有相应的科学库实现了也就二十行代码的事，而且模型训练效果还是比较好的。

那我费这么大劲写的文章是不是没用了？不是的，知其所以然才知其所以然。模型是需要不断地优化的，想要得到一个更切合实际的模型，那就必须不断的优化。

代码+数据
密码:hquq
恳请大家指正批评！