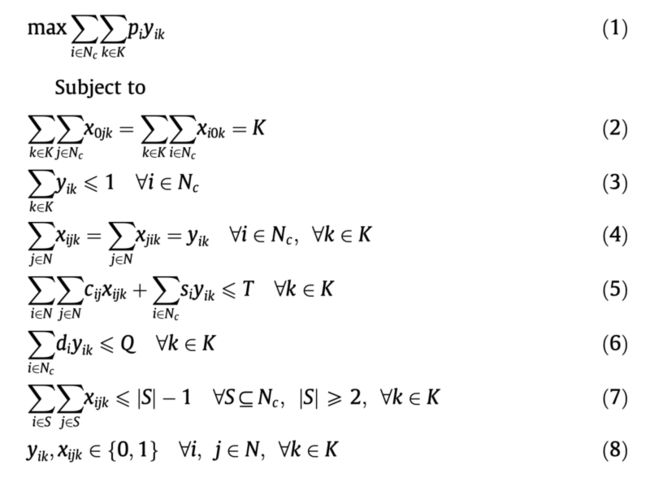1.引言
标准车辆路径问题VRP是把给定的所有顾客指派到对应车辆/载具,确定车辆访问顾客的顺序,使得车辆的行驶里程最小。但在实际应用中,由于资源有限或操作受限等原因,只有一部分顾客能够被服务或访问。这类问题可建模成:给定顾客集合,考虑选择其中的一个子集进行访问,在满足车辆某些运营条件下优化特定目标。Team Orienteering Problems(TOP)就是这样一类问题,其优化目标是:在满足车辆行驶时间不超过给定阈值前提下,最大化访问的顾客的总收益。另一种问题为Profitable Tour Problem(PTP),其优化目标为最大化净收益=收益-行驶费用(和行驶距离相关)。考虑车辆容量约束时,TOP的变体就是Capacitated Team Orienteering Problem(CTOP)。类似地,考虑车辆容量约束的PTP为Capacitated Profitable Tour Problem(CPTP)。
由于TOP是NP-hard的组合优化问题,精确算法在求解大规模问题时比较吃力。本文提出一个通用、新颖的双层启发式算法来求解CTOP:上层通过Filter-and-Fan方法确定要访问的顾客子集来最大化总收益;下层通过变邻域下降(Variable Neighborhood Descent)算法来最小化车辆的总里程。Filter-and-Fan方法结合了禁忌搜索和filter-and-fan Search策略,考虑大邻域结构和多条搜索路径来克服局部最优性。本文提出的Bi-level Filter-and-Fan方法要优于已有的求解CTOP的启发式算法,且在大规模CTOP测试用例上表现出色:能够在较短的计算时间内改进当前已知的最优解。
CTOP可以用一个完全无向图
每条弧(i,j)∈A都对应一个非负费用$c_{ij}$,$c_{ij} = c_{ji}$。共有K辆完全相同的车辆,容量为Q,从仓库出发访问完节点后最终会到仓库。整数规划形式如下
变量$x_{ijk}$ -车辆k是否经过弧(i,j),表示车辆k的访问路径。变量$y_{ik}$-车辆k是否访问节点i。
约束(2)表示一共有K辆车离开仓库,又返回到仓库,限制车辆的总数;
约束(3)限制每个节点最多被访问一次;
约束(4)保证车辆k行驶路径的连通性,如果车辆k访问节点i,那么车辆k一定经过某条边到达节点i、一定经过某条边从节点i出发;
约束(5)限制车辆k的行驶总时间不超过给定阈值T;
约束(6)限制车辆k的装载量不超过其容量Q;
约束(7)限制车辆k访问的路径中没有子回路;
约束(8)限制变量$x_{ijk}$ 、$y_{ik}$为二元变量。
上述整数规划中变量个数随问题规模增加而快速增加:$x_{ijk}$个数为O($n^2$K)、$y_{ik}$个数为O(nK)。
3.求解方法
3.1整体求解框架
本文将CTOP分解为一个主问题-背包问题(knapsack problem),子问题-有容量限制的车辆路径问题(CVRP)。主问题确定要访问的节点子集来最大化总收益,子问题对于给定的节点集合,确定车辆路径即车辆访问节点顺序,来最小化车辆总里程。基于此分解思路,设计双层搜索方法Filter-and-Fan method来求解CTOP。
首先,通过启发式方法构造初始可行解;然后,使用禁忌搜索(Tabu Search)从初始可行解出发得到局部最优解;其次,使用filter-and-fan Search对局部最优解进行改进,得到新的局部最优解;然后对新的局部最优解重复Tabu Search、filter-and-fan Search步骤,直到不能被改进为止。整个求解框架重复、交替进行禁忌搜索(Tabu Search)和filter-and-fan Search,直到局部最优解不能被改进,返回得到的局部最优解。 Bi-level指的是在禁忌搜索和Filter-and-Fan Search中使用变邻域下降算法VND。
3.2构造初始可行解:并行贪婪插入
以仓库为中心,T/2为半径的圆内所有节点为选中的节点,将这些选中的节点按照收益从高到低排序。对每个节点,考虑在每辆车可行的插入位置。迭代地,依次将选中的节点插入到费用最小的位置上,这里费用最小(即“贪婪”)包括两个方面:一方面指车辆的总行驶时间尽可能短,另一方面指车辆的行驶距离尽可能短。直至选中的节点都安排到车辆路径中。初始可行解即为K辆车的访问路径。
3.3上层搜索策略:收益最大化
3.3.1 收益导向的邻域结构
上层搜索策略以最大化选中节点的总收益为目标,因此定义了三种以收益为导向的邻域结构:1–1 Replace, 2–1 Replace and 1–2 Replace。
1–1 Replace:将路径r中某个节点i(被选中的节点/顾客)与一个没有被选中的节点j 交换。在移除节点i前/后,检查节点j可行的插入位置。特别地,如果不需要移除节点i,就找到节点j的可行插入位置,该操作就退化为单点插入;
2–1 Replace:去掉路径中的两个节点(被选中的节点),插入一个未被选中的节点。移除两个被选中的节点后,检查可行的插入位置;
1–2 Replace:去掉路径中的一个节点,插入两个未被选中的节点。移除被选中的节点后,检查可行的插入位置;
上面的操作是去掉被选中的节点,插入未被选中的节点,而每个节点对应收益,这些操作直接影响总收益,所以称为“收益为导向”。从初始可行解出发,使用上述邻域结构,可产生对应的邻域。时间复杂度均为多项式时间,依次为O($n^3$)、O($n^4/2$)、O($n^5/2$)。
在局部搜索过程中,为减少计算时间,评估邻域中解的收益时,只需要考虑受影响的路径(有节点移除、插入),其他不受影响的路径其收益不变。这就需要有特定的数据结构来存储访问过的解的信息,下面的filter-and-fan Search方法可解决该问题。
3.3.2 禁忌搜索(Tabu Search)
禁忌搜索是一种常见的邻域搜索方法,从初始解s出发,迭代从邻域$ϕ_y(s)$中选择不在禁忌列表中的允许解(admissible solution)进行访问,直到满足某个终止条件。禁忌列表来存储最近若干次被访问的解,若禁忌列表中某个解被访问能对目标函数带来较大的提升,该解可被解禁,即从禁忌列表中移除。通过禁忌列表和解禁的操作,跳出局部最优。
这里,有两个参数需要设置:$u_t$--禁忌列表的长度,$z_t$--最大迭代次数。这两个参数影响最终返回的局部最优解的质量。
3.3.3 Filter-and-Fan Search
禁忌搜索可看成单点搜索策略,每次迭代从一个解出发,在其邻域中选择下一个要访问的解。Filter-and-Fan Search可看作多点搜索策略,构造了广度优先的邻域树,每次迭代从树的一层(多个解)向下进行搜索。这里用两个参数来控制邻域树的大小,每层节点(解)个数$n_1$和树的深度L。
Filter-and-Fan搜索考虑更大的邻域,$ϕ_s$={$ϕ_{y1},ϕ_{y2},ϕ_{y3}$},给定当前解s,在邻域$ϕ_s$中寻找收益最高的$n_1$个点。给定根节点$s_0$,在邻域$ϕ_s$中寻找收益最高的$n_1$个点作为第一层的节点;对第l层的某个节点,选择其邻域中收益最高的$n_1$个点,则第i层$n_1$个点,共产生$n_1^2$个候选点。这个过程就像扇子一样,称为fan process。从这$n_1^2$个候选点中,再选择收益最高的$n_1$个点作为第l+1层的节点,这个过程称为filter process。fan process产生邻域树逐层生长的候选点,filter process控制树的每层节点个数。
Filter-and-Fan搜索整体看,类似于多线程的禁忌搜索。同时,借助于树结构记录了搜索过程中访问的每个点,为评估解的收益时只考虑受影响的路径提供了方便。这也是Filter-and-Fan搜索计算时间短的主要原因。
3.4下层搜索策略:距离最小化
针对禁忌搜索或Filter-and-Fan Search产生的解,下层搜索策略以最小化车辆行驶(路径)总里程为目标,采用有序搜索方式进行改进。下层搜索策略考虑交换边的邻域结构:2-Opt、1–1 Exchange、1–0 Relocate,将这三种邻域结构依次标号为1、2、3。首先尝试标号1的邻域结构,如果找到更优解(距离更短),从更优解继续迭代;否则,依次尝试标号高的邻域2、3,若在标号最大的邻域,都没有找到更优的解,搜索终止。
其中,2-Opt:交换同一条路径上的两条边;1–1 Exchange:交换不同路径上的两条边;1–0 Relocate:去掉一条路径上的边,插入到另一条路径上。
4.计算实验
4.2 参数设置和实证分析
采用130个前人论文中使用的CTOP实例,进行实验,从解的质量(相对当前已知最优解的偏离百分比)、求解时间两个方面分析算法参数的影响。其中,相对当前已知最优解的偏离百分比=(当前已知最优解对应收益-算法求出解对应收益)/当前已知最优解对应收益*100%。
4.2.1 禁忌搜索效果分析
考虑禁忌列表长度$u_t$、最大迭代次数$z_t$对求解的影响。这里,在整体搜索框架Algorithm1中不使用Filter-and-Fan Search,只考虑禁忌搜索。
单独使用禁忌搜索在将近10s时间内可以改进当前已知最优解0.01%($u_t$ = 30 and $z_t$ = 6000)。
4.2.2 Filter-and-Fan Search效果分析
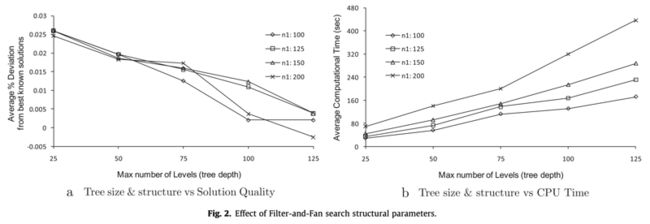
单独使用Filter-and-Fan Search,讨论参数邻域树每层节点个数$n_1$和树的深度L对求解的影响。
当每层节点个数=200,树的深度=125时,可以改进当前已知最优解0.01%。考虑到计算时间,每层节点个数=100、树的深度=100看起来是不错的选择。
4.2.3 组合效果分析
结合使用禁忌搜索和Filter-and-Fan Search,正如Algorithm1中所示Bi-level Filter-and-Fan method,固定参数$n_1$=100、L=100,考虑禁忌搜索参数$u_t$、$z_t$的组合影响。
Bi-level Filter-and-Fan method平均在6.83s内可改进当前已知最优解0.012%,且迭代次数少于1000次($u_t$ = 30, $z_t$ = 750, $n_1$ = 100,L = 100)。而单独使用禁忌搜索改进当前最优解0.01%需要迭代6000次,时间将近10s($u_t$ = 30 and $z_t$ = 6000)。
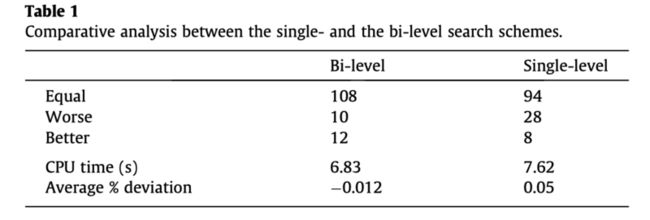
4.2.4 双层搜索机制的效果分析
single-level指的是在禁忌搜索和Filter-and-Fan Search中不使用变邻域下降算法VND。
在求解时间、解的质量方面,双层搜索机制都要优于单层搜索机制。
4.3 CTOP测试用例上求解结果对比
BiF&F-s、BiF&F-f表示双层搜索机制的两种不同参数配置:s-slow($z_t$ = 10,000, $u_t$ = 30, $n_1$ = 100 and L = 100),f-fast($z_t$ = 750, $u_t$ = 30, $n_1$ = 100, L = 100)。BiF&F-b代表BiF&F使用各种参数配置得得到的最佳解,b-best。
采用BiF&F-s、BiF&F-f和前人论文Archetti et al. (2009)中提出的启发式算法VNS、TSf在130个测试用例上进行对比。部分结果如下
注:BK-已知最优解(best known results);p-总收益(total profit), t-计算时间(computational time),%D-相对已知最优解BK的偏离百分比。
BiF&F-f、BiF&F-s在130个CTOP测试用例上表现出色:BiF&F-f可以在6.83s(平均)内对已知最优解BK的改进为0.012%,获得12个新的最优解;BiF&F-s可在14.36s内对已知最优解改进为0.04%,获得18个新的最优解。
4.4 大规模CTOP实例上表现
BiF&F-f在大规模CTOP实例上得到的解与最佳解的平均偏离为0.18%,最大偏离低于2.52%,平均计算时间为1365s。BiF&F-s与最佳解的平均偏离为0.01%,最大偏离不超过0.53%,平均计算时间为4,657.76s。部分结果如下