Introduction to CELP Coding
Introduction to CELP Coding
Do not meddle in the affairs of poles, for they are subtle andquick to leave the unit circle.Speex is based on CELP, which stands for Code Excited Linear Prediction.This section attempts to introduce the principles behind CELP, soif you are already familiar with CELP, you can safely skip to section 8. The CELP technique is based on threeideas:
- The use of a linear prediction (LP) model to model the vocal tract
- The use of (adaptive and fixed) codebook entries as input (excitation)of the LP model
- The search performed in closed-loop in a ``perceptually weighteddomain''
This section describes the basic ideas behind CELP. This is stilla work in progress.
Source-Filter Model of Speech Prediction
The source-filter model of speech production assumes that the vocalcords are the source of spectrally flat sound (the excitation signal),and that the vocal tract acts as a filter to spectrally shape thevarious sounds of speech. While still an approximation, the modelis widely used in speech coding because of its simplicity.Its useis also the reason why most speech codecs (Speex included) performbadly on music signals. The different phonemes can be distinguishedby their excitation (source) and spectral shape (filter). Voiced sounds(e.g. vowels) have an excitation signal that is periodic and thatcan be approximated by an impulse train in the time domain or by regularly-spacedharmonics in the frequency domain. On the other hand, fricatives (suchas the "s", "sh" and "f"sounds) have an excitation signal that is similar to white Gaussiannoise. So called voice fricatives (such as "z" and"v") have excitation signal composed of an harmonicpart and a noisy part.
The source-filter model is usually tied with the use of Linear prediction.The CELP model is based on source-filter model, as can be seen fromthe CELP decoder illustrated in Figure 1.
Linear Prediction (LPC)
Linear prediction is at the base of many speech coding techniques,including CELP. The idea behind it is to predict the signal ![]() using a linear combination of its past samples:
using a linear combination of its past samples:
![$\displaystyle y[n]=\sum_{i=1}^{N}a_{i}x[n-i]$](http://img.e-com-net.com/image/product/ce519cd1eeee483293c2c230b155deca.png)
where ![]() is the linear prediction of
is the linear prediction of ![]() . The predictionerror is thus given by:
. The predictionerror is thus given by:
![$\displaystyle e[n]=x[n]-y[n]=x[n]-\sum_{i=1}^{N}a_{i}x[n-i]$](http://img.e-com-net.com/image/product/ea0dbdb11b8948a4946295c9344ad6b8.png)
The goal of the LPC analysis is to find the best prediction coefficients![]() which minimize the quadratic error function:
which minimize the quadratic error function:
![$\displaystyle E=\sum_{n=0}^{L-1}\left[e[n]\right]^{2}=\sum_{n=0}^{L-1}\left[x[n]-\sum_{i=1}^{N}a_{i}x[n-i]\right]^{2}$](http://img.e-com-net.com/image/product/94dd5a8a9c914038afc7a3d7ad798f23.png)
That can be done by making all derivatives
![]() equal to zero:
equal to zero:
![$\displaystyle \frac{\partial E}{\partial a_{i}}=\frac{\partial}{\partial a_{i}}\sum_{n=0}^{L-1}\left[x[n]-\sum_{i=1}^{N}a_{i}x[n-i]\right]^{2}=0$](http://img.e-com-net.com/image/product/5476cabbc9914b25a02a8292ce4c6c51.png)
For an order ![]() filter, the filter coefficients
filter, the filter coefficients ![]() are foundby solving the system
are foundby solving the system ![]() linear system
linear system
![]() ,where
,where
![$\displaystyle \mathbf{R}=\left[\begin{array}{cccc}R(0) & R(1) & \cdots & R(N-1......& \vdots & \ddots & \vdots\\R(N-1) & R(N-2) & \cdots & R(0)\end{array}\right]$](http://img.e-com-net.com/image/product/457be9410a77419c815e74159f51a654.png)
![$\displaystyle \mathbf{r}=\left[\begin{array}{c}R(1)\\R(2)\\\vdots\\R(N)\end{array}\right]$](http://img.e-com-net.com/image/product/994aa45d582548cf822076da97ce93e2.png)
with ![]() , the auto-correlation of thesignal
, the auto-correlation of thesignal ![]() , computed as:
, computed as:
![$\displaystyle R(m)=\sum_{i=0}^{N-1}x[i]x[i-m]$](http://img.e-com-net.com/image/product/d84f91edb48247458d2c47e6eb0b5027.png)
Because
![]() is toeplitz hermitian, the Levinson-Durbinalgorithm can be used, making the solution to the problem
is toeplitz hermitian, the Levinson-Durbinalgorithm can be used, making the solution to the problem
![]() instead of
instead of
![]() . Also, it can be proventhat all the roots of
. Also, it can be proventhat all the roots of ![]() are within the unit circle, which meansthat
are within the unit circle, which meansthat ![]() is always stable. This is in theory; in practice becauseof finite precision, there are two commonly used techniques to makesure we have a stable filter. First, we multiply
is always stable. This is in theory; in practice becauseof finite precision, there are two commonly used techniques to makesure we have a stable filter. First, we multiply ![]() by a numberslightly above one (such as 1.0001), which is equivalent to addingnoise to the signal. Also, we can apply a window to the auto-correlation,which is equivalent to filtering in the frequency domain, reducingsharp resonances.
by a numberslightly above one (such as 1.0001), which is equivalent to addingnoise to the signal. Also, we can apply a window to the auto-correlation,which is equivalent to filtering in the frequency domain, reducingsharp resonances.
Pitch Prediction
During voiced segments, the speech signal is periodic, so it is possibleto take advantage of that property by approximating the excitationsignal ![]() by a gain times the past of the excitation:
by a gain times the past of the excitation:
where ![]() is the pitch period,
is the pitch period, ![]() is the pitch gain. We callthat long-term prediction since the excitation is predicted from
is the pitch gain. We callthat long-term prediction since the excitation is predicted from ![]() with
with ![]() .
.
Innovation Codebook
The final excitation ![]() will be the sum of the pitch predictionand an innovation signal
will be the sum of the pitch predictionand an innovation signal ![]() taken from a fixed codebook,hence the name Code Excited Linear Prediction. The final excitationis given by:
taken from a fixed codebook,hence the name Code Excited Linear Prediction. The final excitationis given by:
The quantization of ![]() is where most of the bits in a CELP codecare allocated. It represents the information that couldn't be obtainedeither from linear prediction or pitch prediction. In the z-domainwe can represent the final signal
is where most of the bits in a CELP codecare allocated. It represents the information that couldn't be obtainedeither from linear prediction or pitch prediction. In the z-domainwe can represent the final signal ![]() as
as
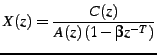
Noise Weighting
Most (if not all) modern audio codecs attempt to ``shape'' thenoise so that it appears mostly in the frequency regions where theear cannot detect it. For example, the ear is more tolerant to noisein parts of the spectrum that are louder and vice versa. Inorder to maximize speech quality, CELP codecs minimize the mean squareof the error (noise) in the perceptually weighted domain. This meansthat a perceptual noise weighting filter ![]() is applied to theerror signal in the encoder. In most CELP codecs,
is applied to theerror signal in the encoder. In most CELP codecs, ![]() is a pole-zeroweighting filter derived from the linear prediction coefficients (LPC),generally using bandwidth expansion. Let the spectral envelope berepresented by the synthesis filter
is a pole-zeroweighting filter derived from the linear prediction coefficients (LPC),generally using bandwidth expansion. Let the spectral envelope berepresented by the synthesis filter ![]() , CELP codecs typicallyderive the noise weighting filter as:
, CELP codecs typicallyderive the noise weighting filter as:
where
![]() and
and
![]() in the Speex referenceimplementation. If a filter
in the Speex referenceimplementation. If a filter ![]() has (complex) poles at
has (complex) poles at ![]() in the
in the ![]() -plane, the filter
-plane, the filter
![]() will have its poles at
will have its poles at
![]() , making it a flatter version of
, making it a flatter version of ![]() .
.
The weighting filter is applied to the error signal used to optimizethe codebook search through analysis-by-synthesis (AbS). This resultsin a spectral shape of the noise that tends towards ![]() . Whilethe simplicity of the model has been an important reason for the successof CELP, it remains that
. Whilethe simplicity of the model has been an important reason for the successof CELP, it remains that ![]() is a very rough approximation forthe perceptually optimal noise weighting function. Fig. 2illustrates the noise shaping that results from Eq. 1.Throughout this paper, we refer to
is a very rough approximation forthe perceptually optimal noise weighting function. Fig. 2illustrates the noise shaping that results from Eq. 1.Throughout this paper, we refer to ![]() as the noise weightingfilter and to
as the noise weightingfilter and to ![]() as the noise shaping filter (or curve).
as the noise shaping filter (or curve).
Analysis-by-Synthesis
One of the main principles behind CELP is called Analysis-by-Synthesis(AbS), meaning that the encoding (analysis) is performed by perceptuallyoptimising the decoded (synthesis) signal in a closed loop. In theory,the best CELP stream would be produced by trying all possible bitcombinations and selecting the one that produces the best-soundingdecoded signal. This is obviously not possible in practice for tworeasons: the required complexity is beyond any currently availablehardware and the ``best sounding'' selection criterion impliesa human listener.
In order to achieve real-time encoding using limited computing resources,the CELP optimisation is broken down into smaller, more manageable,sequential searches using the perceptual weighting function describedearlier.
linking: http://www.speex.org/docs/manual/speex-manual/node9.html
![\includegraphics[width=0.45\paperwidth,keepaspectratio]{celp_decoder}](http://img.e-com-net.com/image/product/2cc77b3f430942ccadc579505f788929.png)
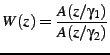
![\includegraphics[width=0.45\paperwidth,keepaspectratio]{ref_shaping}](http://img.e-com-net.com/image/product/cd48e67e9c41435ebdb8a41c50d3669a.png)