1. 定义
红黑树也是二叉查找树,我们知道,二叉查找树这一数据结构并不难,而红黑树之所以难是难在它是自平衡的二叉查找树,在进行插入和删除等可能会破坏树的平衡的操作时,需要重新自处理达到平衡状态。红黑树是一种含有红黑结点并能自平衡的二叉查找树,又称黑色完美平衡。
动画演示:https://rbtree.phpisfuture.com/
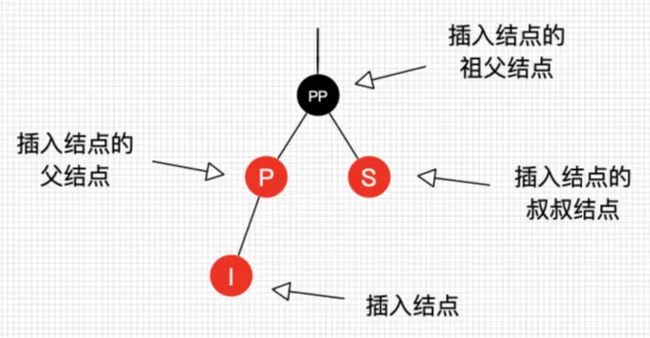
2. 节点称呼
3. 性质
-
每个节点要么是黑色,要么是红色。
-
根节点一定是黑色。
-
每个叶子节点(nil或null)都是黑色的。
-
每个红节点的两个子节点一定是黑色的。(不可以同时存在两个相连的红结点,即:红节点的父结点与子结点都是黑的)
-
从任意节点出发到每个叶子节点的路径都包含相同个数的黑色节点。
* 如果一个结点存在黑子结点,那么该结点肯定有两个子结点。 * 黑色完美平衡。
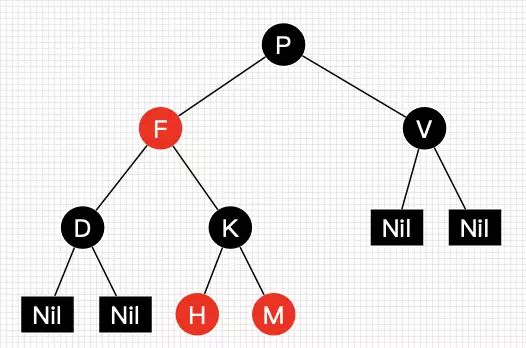
下面是一棵简单的红黑树,Nil(java中为null)是叶子节点并为黑色:
上图中的红黑树并不是完美平衡的二叉查找树,P节点的左边比右边高,但是左右黑色的层数是相等的,任意一个结点到叶子节点的黑色节点数都相同(性质5),也被成为黑色完美平衡。
4. 红黑树的自平衡
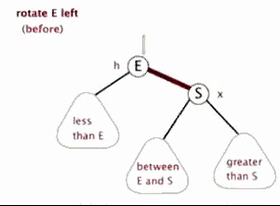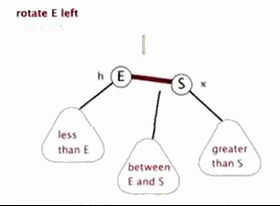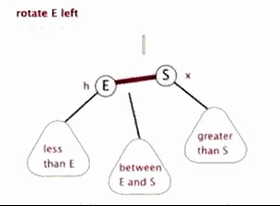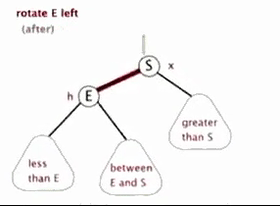
4.1 左旋
以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,其他结点保持不变。
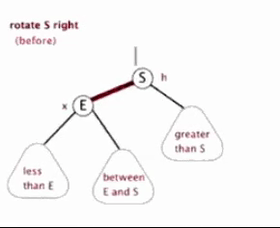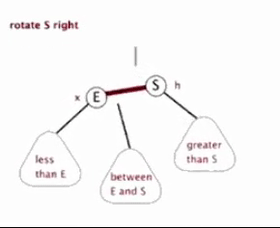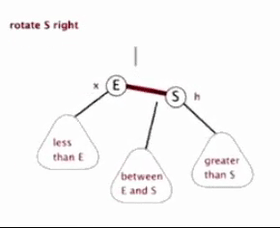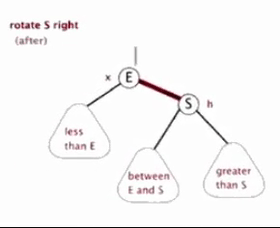
4.2 右旋
以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,其他结点保持不变。
4.3 变色
结点的颜色由红变黑或由黑变红。
5. 红黑树的查找
红黑树是一颗二叉平衡树,查找不会破坏平衡性,所以和二叉平衡术查找方式一致。
- 从根节点开始查找,为空就返回null,为当前值就返回,否则继续向下查找。
- 如果当前节点的key为要查找的节点的key,那么直接返回当前值。
- 如果当前节点的key大于要查找的节点的key,那么继续向当前节点的左子节点查找。
- 如果当前节点的key小于要查找的节点的key,那么继续向当前节点的右子节点查找。
6. 红黑树的插入
插入会破坏红黑树的黑色完美平衡,所以插入第一步要找到要插入的位置进行插入,第二步进行自平衡。
6.1 查找插入位置
所有插入操作都是在叶子结点进行的。
- 插入节点的颜色肯定为红色。因为插入节点为黑色,就会破坏黑色完美平衡,使得到叶子节点的黑色数+1,而红色不会破坏。
- 基本与红黑树的查找相同:
从根节点开始,如果根节点为空,则插入在根节点,否则根节点为当前节点。
- 如果当前节点为null,则返回当前节点的父节点进行插入。
- 如果当前节点的key等与插入节点的key,则更新当前节点的value。
- 如果当前节点的key大于插入节点的key,则继续向当前节点的左子节点继续查找。
- 如果当前节点的key小于插入节点的key,则继续向当前节点的右子节点继续查找。
6.2 插入的自平衡
插入主要指针指向插入结点,通过4. 红黑树的自平衡将红黑树达到的平衡即可
左旋
条件:当前节点的父节点是红色 & 当前节点的叔叔节点是黑色或者不存在 & 当前结点是其父节点的右子结点。
步骤:
- 将父节点左旋
- 将指针指向父结点
右旋
条件:当前节点的父节点是红色 & 当前节点的叔叔节点是黑色或者不存在 & 当前结点是其父节点的左子结点。
步骤:
- 将父节点变为黑色
- 将祖父结点变为红色
- 将祖父结点右旋
- 将指针指向祖父结点
变色
条件:当前节点的父节点是红色并且当前节点的叔叔节点也是红色。
步骤:
- 当前结点是根结点直接变为黑色
- 当前结点不是根结点
- 将父节点与叔叔节点变为黑色
- 将祖父结点变为红色
- 将指针指向祖父结点
JDK1.8中插入自平衡的源码实现:
private void fixAfterInsertion(Entry x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
// 插入的父节点是左子节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// y是插入节点的祖父节点的右子节点(叔叔节点)
Entry y = rightOf(parentOf(parentOf(x)));
// y是红色
if (colorOf(y) == RED) {
// 变色处理
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
// 指针指向插入节点的祖父节点
x = parentOf(parentOf(x));
} else {
// y是黑色的
// 插入节点是是父节点的右子节点
if (x == rightOf(parentOf(x))) {
// 父节点左旋
x = parentOf(x);
rotateLeft(x);
}
// 插入节点是是父节点的左节点
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
// 祖父节点右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
// 插入的父节点是右子节点
// y是插入节点的祖父节点的左子节点(叔叔节点)
Entry y = leftOf(parentOf(parentOf(x)));
// y是红色
if (colorOf(y) == RED) {
// 变色处理
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
// 指针指向插入节点的祖父节点
x = parentOf(parentOf(x));
} else {
// 插入节点是是父节点的左子节点
if (x == leftOf(parentOf(x))) {
// 父亲节点右旋
x = parentOf(x);
rotateRight(x);
}
// 插入节点是是父节点的右子节点
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
// 祖父节点左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
7. 红黑树删除
删除操作与插入差不多,查找、删除、自平衡。查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;当存在目标结点时,删除后就得做自平衡处理了。删除了结点后我们还需要找结点来替代删除结点的位置,不然子树跟父辈结点断开了,除非删除结点刚好没子结点,那么就不需要替代。
7.1 查找删除位置
基本与红黑树的查找相同:
- 从根节点开始,如果根节点为空,则删除在根节点,否则根节点为当前节点。
- 如果当前节点为null,则返回当前节点的父节点进行插入。
- 如果当前节点的key等与删除节点的key,则找到当前节点。
- 如果当前节点的key大于删除节点的key,则继续向当前节点的左子节点继续查找。
- 如果当前节点的key小于删除节点的key,则继续向当前节点的右子节点继续查找。
7.2 删除结点
删除节点的可能情况:
JDK1.8中TreeMap删除可能性源代码实现:
private void deleteEntry(Entry p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
// 如果删除节点有两个子节点
if (p.left != null && p.right != null) {
// 找到替代节点(很简单,自己看TreeMap源码)
Entry s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
// 如果有一个替换节点
Entry replacement = (p.left != null ? p.left : p.right);
// 如果存在替换节点
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
}
// 如果删除节点是根节点
else if (p.parent == null) { // return if we are the only node.
root = null;
} else {
// 没有子节点
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
7.3 删除后的自平衡
删除自平衡处理:
JDK1.8中TreeMap删除自平衡源代码实现:
private void fixAfterDeletion(Entry x) {
while (x != root && colorOf(x) == BLACK) {
// 删除节点是左子节点
if (x == leftOf(parentOf(x))) {
// sib是删除节点父节点的右子节点(兄弟节点)
Entry sib = rightOf(parentOf(x));
// 兄弟节点是红色
if (colorOf(sib) == RED) {
// 情况1.1处理
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
// sib兄弟节点有两个黑色的子节点,情况2处理
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
// 变色
setColor(sib, RED);
// 指针指向删除节点的父节点
x = parentOf(x);
} else {
// 兄弟节点的右子节点是黑色
if (colorOf(rightOf(sib)) == BLACK) {
// 情况3.1.1处理
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// 情况3.1.2处理
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
// 跳出循环
x = root;
}
} else { // symmetric
// 删除节点是右子节点
// sib是删除节点父节点的左子节点(兄弟节点)
Entry sib = leftOf(parentOf(x));
// 兄弟节点是红色
if (colorOf(sib) == RED) {
// 情况1.2处理
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
// sib兄弟节点有两个黑色的子节点,情况2处理
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
// 变色
setColor(sib, RED);
// 指针指向删除节点的父节点
x = parentOf(x);
} else {
// 兄弟节点的左子节点是黑色
if (colorOf(leftOf(sib)) == BLACK) {
// 情况3.2.1处理
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
// 情况3.2.2处理
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
// 跳出循环
x = root;
}
}
}
setColor(x, BLACK);
}
参考
- https://www.phpisfuture.com/article/1
- https://www.jianshu.com/p/e136ec79235c
结语
欢迎关注微信公众号『码仔zonE』,专注于分享Java、云计算相关内容,包括SpringBoot、SpringCloud、微服务、Docker、Kubernetes、Python等领域相关技术干货,期待与您相遇!
![]()