CSP-J2019普及组复赛T4——加工零件

题目描述

凯凯的工厂正在有条不紊地生产一种神奇的零件，神奇的零件的生产过程自然也很神奇。

工厂里有 $n$ 位工人，工人们从 $1$∼$n$ 编号。

某些工人之间存在双向的零件传送带。

保证每两名工人之间最多只存在一条传送带。

如果 $x$号工人想生产一个被加工到第 $L(L>1)$ 阶段的零件，则所有与 $x$ 号工人有传送带直接相连的工人，都需要生产一个被加工到第 $L-1$ 阶段的零件（但 $x$ 号工人自己无需生产第 $L-1$ 阶段的零件）。

如果 $x$号工人想生产一个被加工到第 $1$ 阶段的零件，则所有与 $x$ 号工人有传送带直接相连的工人，都需要为 $x$号工人提供一个原材料。

轩轩是 $1$ 号工人。

现在给出 $q$ 张工单，第 $i$ 张工单表示编号为$a_i$ 的工人想生产一个第 $L_i $阶段的零件。

轩轩想知道对于每张工单，他是否需要给别人提供原材料。

他知道聪明的你一定可以帮他计算出来！

输入格式
第一行三个正整数 $n$，$m$ 和 $q$，分别表示工人的数目、传送带的数目和工单的数目。

接下来 $m$ 行，每行两个正整数 $u$ 和 $v$，表示编号为 $u$ 和 $v$ 的工人之间存在一条零件传输带。保证 $u\ne v$。

接下来 $q$ 行，每行两个正整数 $a$ 和 $L$，表示编号为 $a$ 的工人想生产一个第 $L$ 阶段的零件。

输出格式
共 $q$ 行，每行一个字符串 “Yes” 或者 “No”。如果按照第 $i$ 张工单生产，需要编号为 1 的轩轩提供原材料，则在第 $i$ 行输出 “Yes”；否则在第 $i$ 行输出 “No”。注意输出不含引号。

输入样例：

3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2

输出样例：

No
Yes
No
Yes
No
Yes

算法思想

性质1
询问轩轩($1$号工人)否需要给别人（$a_i$号工人）提供原材料，可以理解为从图中顶点$1$到$a_i$是否存在一条长度为L的路径。
例如下图中，顶点$1$到$3$中存在一条长度为2的路径，所以当$3$号工人生成2阶段的零件时，需要$1$号工人提供原材料。

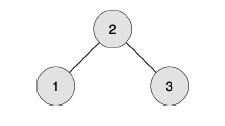
顶点$1$到$3$中不存在一条长度为3的路径，所以当$3$号工人生成3阶段的零件时，不需要$1$号工人提供原材料。

性质2
进一步思考，如果顶点u到v中存在$1$条长度为L的路径，那么也一定存在长度为L + 2、L + 4、L + 6…的路径。因为图中的边是双向的，那么可以选择路径中选择某些顶点，让其经历多次即可。
即如果两个顶点之间存在一条长度是L$(L>0)$的路径，那么就一定可以构造出所有长度大于等于L，且奇偶性和L相同的路径。
这样只要求出1点到顶点u的最短路径dist，如果dist和L奇偶性相同，并且L>=dist，那么1到顶点u之间存在一条长度是L的路径。

因为从1点到其它顶点u可能存在不止一条路径，其中有路径长度为偶数的、也可能有长度为奇数的，那么就需要分别求出到u点的长度为偶数的最短路径长度dist[u][0]和长度为奇数的路径长度dist[u][1]。
如果到u的路径长度为L为偶数、且L >= dist[u][0]，那么1到顶点u之间存在一条长度是L的路径。
如果到u的路径长度为L为奇数、且L >= dist[u][1]，那么1到顶点u之间存在一条长度是L的路径。

算法实现

由以上两个性质：

1. 使用BFS算法求出1点到任一点u长度为偶数的最短路径dist[u][0]和长度为奇数的最短路径dist[u][1]。
2. 判断对于q个询问中，到u点路径长度为L时，如果L是偶数，并且L >= dist[u][0]，则需要提供原材料；如果L是奇数，并且L >= dist[u][1]，则需要提供原材料。否则不需要提供原材料。
3. 特殊情况，当1号点与其他点均不连通，由于输入时 L >= 1，因此直接输出"No"即可。

时间复杂度

$O(n+m+q)=3\times 10^5$

代码实现

#include 
#include 
#include 
using namespace std;

const int N = 100010, M = 2 * N;

int h[N], e[M], ne[M], idx;
int dist[N][2], q[M];

void add(int a, int b)
{
     
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void bfs()
{
     
    memset(dist, 0x3f, sizeof dist);
    //到1点经过0条边时到达自己时最短路径长度为0
    dist[1][0] = 0; 
    
    int hh = 0, tt = 0;
    q[tt] = 1;
    
    while(hh <= tt)
    {
     
        int u = q[hh ++];
        
        for(int i = h[u]; ~i; i = ne[i])
        {
     
            int v = e[i];
            
            //从u点经过奇数条边扩展到v，如果能进行松弛，则更新dist[v][0]
            if(dist[v][0] > dist[u][1] + 1)
            {
     
                dist[v][0] = dist[u][1] + 1;
                q[++ tt] = v;
            }
            //从u点经过偶数条边扩展到v，如果能进行松弛，则更新dist[v][1]
            if(dist[v][1] > dist[u][0] + 1)
            {
     
                dist[v][1] = dist[u][0] + 1;
                q[++ tt] = v;
            }            
        }
    }
}

int main()
{
     
    int n, m, q;
    cin >> n >> m >> q;
    
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++)
    {
     
        int u, v;
        cin >> u >> v;
        add(u, v), add(v, u);
    }
    
    bfs();
    
    while(q --)
    {
     
        int u, L;
        cin >> u >> L;
        if(h[1] == -1) puts("No"); //判断1点是否与其它点连通
        else if(dist[u][L & 1] <= L) puts("Yes");
        else puts("No");
    }
    
    return 0;
}