2011 Multi-University Training Contest 3 - Host by BIT
T1:Inverting Cups
题意是给出A个杯子,一开始都朝上,每次可以翻B个杯子,问最少需要翻转多少次可以让所有杯子都朝下。
分类讨论:
首先对于A%B==0一类情况,直接输出。
对于A>=3B,让A减到[2B,3B)区间内,翻转次数累加上A/B-2。
当A>=2B时,分奇偶讨论:A为奇数B为偶数显然无解;AB同奇偶时最多需要3次,A偶数B奇数最多需要4次。
当A<2B时,分奇偶讨论:AB同奇偶时最多需要3次,A奇数B偶数无解,A偶数B奇数时,有F(A,B)=F(A,A-B)成立,可以转换成上面的情况求解即可。
具体证明画画图就知道了,将两个B分别放到对称的位置上,想办法调整使得每次改变自己需要的杯子就行。对于A偶B奇的F(A,B)=F(A,A-B),其实挺好想的,因为A是偶数,B是奇数,而每个杯子一共翻转了奇数次,而一共一定是要翻转偶数轮,因此每个杯子不翻转的次数也是奇数次,也就相当于对“翻转”操作“取反”,每次翻转A-B个,结果是一样的,因此F(A,B)=F(A,A-B)成立。
另外:注意cin,cout超时。。。。。。
T3:The King’s Problem
题意是给出一张有向图,然后将这张图分成若干部分,使得每部分中的点之间都有路径相连(至少有一个方向相连),问最少能分成几部分。
最小路径覆盖问题,首先将有向图的强连通分量缩点,然后二分图匹配一遍,用点数减去最大匹配就是最小路径覆盖数。路径覆盖的概念请自行百度百科。
注意缩点以后对于同一个强连通分量内的边不要加上。
T4:The Lost Traveler
就是给一个角度序列,负数代表逆时针正数顺时针,一个机器人从原点出发一直走,不能停,按这个序列转弯,转弯位置可以任意选,求最后能不能够走回原点。
由于转弯处可以任选,即每条走的直线可以平移,故每次转弯可达区域是一个范围。如下图阴影:
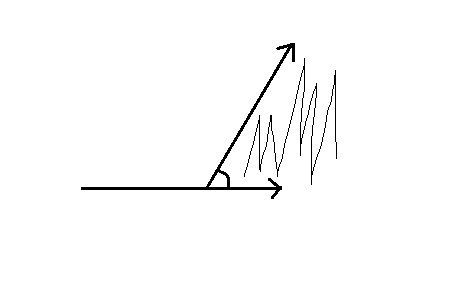
假设出发时水平向右走,它的可达范围是 x 轴正半轴0度(注意没有原点),第一次转弯,可达范围变为转后方向线与x 轴正向的夹角之间,并且方向线可平移至原点。以后每次转弯,都只会在可达角度之间或将可达范围扩大。故最终可达位置一定是一个连续的扇形开区间。
当这个开区间的范围大于180度的时候(等于的话,如果偏离过x轴再水平返回肯定是不行的,所以至少要多),才能覆盖到原点,即可以回去。
两点注意,一个是读入的角度从-360度到360度,实际需要考虑的范围只有-180度到180度,转多了其实是一回事且不好判断,故可进行一下转换。
另一点是一个特殊情况,就是出发以后直接调头回来,这个需要特判。
一个游戏,如下图。
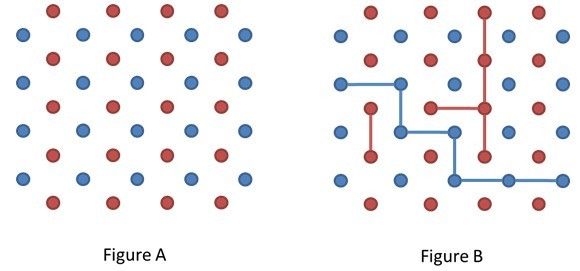
蓝方和红方动想办法使得自己最先连到对岸。每次可以选择同色的两个点连接起来。
给出一张图的大小,双方都采取最优策略,问是先手必胜还是后手必胜。
显然先手胜,因为先手下一条边以后既会巩固自己的优势又会阻碍对方的发展,而开始时双方是完全均势,因此先手必胜。
T6:D_num
读入一个n,判断n是否恰好有4个约数。n非常大(10^18)
对于这样的n只有两种情况:
1、n是两个不同质数的乘积
2、n是一个质数的三次方
于是用很牛逼很伟大的一种模板可以迅速跑出N的一个最小约数,然后判断水过。详见
http://hi.baidu.com/buaa_babt/blog/item/34d9ac86dd80dcc39023d91f.html
T7:A Hard Journey
读入一个N*N的矩阵,矩阵的每个格子都是M*M的01矩阵,有一种武器可以一次打掉小矩阵内目标方向的一行1,打一次需要p,换方向需要q,每次必须要打完一个小矩阵才能去下一个矩阵,并且必须要炮的方向和前进方向一致才能走(详细请看题目,不太好描述),问从(1,1)走到(N,N)最小需要消耗多少体力。
对于每个小格子,如果只横着打或者只竖着打都好做,判断一行里或者一列里有没有1即可。对于横竖都打的情况求解最小值,就是一个二分图最大匹配的问题(最小点覆盖),最后加上换方向的代价就行。
对于每个格子要往下一个格子转移,最好每种情况一个一个列出来,这样不容易错。我就是因为状态转移WA了一次。
每个格子存两个状态,打完以后方向向下和打完以后方向向右。转移就明了了吧。不再赘述,详见代码。
T8 Moonfang's Birthday
对于IMPOSSIBLE,只有一种可能,就是所有人的钱加起来也不够,其他任何情况都能拼出一种方案。
然后,就是尽量让所有人交的钱尽量接近p/n,如果钱少的不够平均值,就全出。因为钱数最少的人是最有可能确定自己应该出多少钱的,所以对ai排序,从小到大考虑。考虑完一个人,由于需要让出钱最多的人出钱尽量少,所以,每次的平均值为last/(n-i),接着,为了让钱数最多的人把剩下的钱出了,就在每次除法时下取整。这样不够每人分的钱就会均到总钱数最多的人身上,最后要考虑分配结果可能和初始排序有关,所以,在最开始排序的时候把下标带上作为第二引索。
这道题的贪心特点是:不能通过每个条件去考虑用怎样的方案。只能通过感觉设计一个贪心方案,然后通过调整来适应所有的条件。
T9 Light and Shadow
最简单的模拟做法是枚举所有的角度,然后看这个光线照到哪里。但是只要数据过大,枚举时间就会超,而且由于精度问题,很可能跳过了一个很小的区间。
如果先把点离散化,就不能处理一条线段的两端被挡住的情况。另外,枚举照到没一条线段的时候,要枚举是否被其他线段挡住。会很慢。如果换成角度的话,就可以看成一段一段的区间覆盖,对于环形的线段要考虑分成两段加入线段树,同时,考虑每条线段的起点和终点如何区分(看起点到终点之间的角是否小于PI/2)。这样用线段树来做就可以了,但是一直WA,不知错在哪里,就不贴代码了。
T10 The Triangle ransmitter
给N个平面上的点,找三个点,使两两距离之和最小,可以不是三角形。。Orz(Barty乃是肿么读的题。。T_T)
和最近点对的做法一样,分治。
P1001
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
__int64 f(__int64 a, __int64 b)
{
__int64 res = 0;
if (a % b == 0) return a / b;
if (a >= 3 * b)
{
res += a / b - 2;
a = (a % b) + 2 * b;
}
if (a >= 2 * b)
{
if (a % 2 == b % 2) res += 3;
else if (a % 2 == 0) res += 4;
else res = -1;
}
else if ((a % 2 == b % 2)) res += 3;
else if (a % 2 == 0)
{
return f(a, a - b);
}
else res = -1;
return res;
}
__int64 a, b;
int main()
{
while (~scanf("%I64d%I64d", &a, &b))
{
__int64 res = f(a, b);
if (res > 0) printf("%I64d\n", res);
else printf("No Solution!\n");
}
return 0;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#define N 5010
#define M 100010
using namespace std;
struct edge
{
int v, next;
}e[M];
int p[N], eid, n, m;
void mapinit()
{
eid = 0;
memset(p, -1, sizeof(p));
}
void insert(int x, int y)
{
e[eid].v = y;
e[eid].next = p[x];
p[x] = eid++;
}
int dfn[N], low[N], stack[N], belong[N];
int bcnt, dindex = 0, top = 0;
bool instack[N];
void tarjan(int v)
{
instack[v] = true;
stack[++top] = v;
dfn[v] = low[v] = ++dindex;
for (int i = p[v]; i != -1; i = e[i].next)
{
if (!dfn[e[i].v])
{
tarjan(e[i].v);
low[v] = min(low[v], low[e[i].v]);
}
else if (instack[e[i].v])
{
low[v] = min(low[v], dfn[e[i].v]);
}
}
int temp;
if (dfn[v] == low[v])
{
bcnt++;
do{
temp = stack[top--];
instack[temp] = false;
belong[temp] = bcnt;
}while (temp != v);
}
}
void solve()
{
memset(dfn, 0, sizeof(dfn));
top = bcnt = dindex = 0;
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
}
bool use[N];
int match[N];
bool hungary(int v)
{
for (int i = p[v]; i != -1; i = e[i].next)
{
int u = e[i].v;
if (!use[u])
{
use[u] = true;
int temp = match[u];
match[u] = v;
if (temp == 0 || hungary(temp)) return true;
match[u] = temp;
}
}
return false;
}
int calc()
{
memset(match, 0, sizeof(match));
int cnt = 0;
for (int i = 1; i <= n; i++)
{
memset(use, false, sizeof(use));
if (hungary(i)) cnt++;
}
return cnt;
}
void print_map()
{
for (int i = 1; i <= n; ++i)
{
printf("%d: ", i);
for (int j = p[i]; j != -1; j = e[j].next)
printf("%d, ", e[j].v);
printf("\n");
}
}
bool map[N][N];
int main()
{
// freopen("input.in", "r", stdin);
int T;
scanf("%d", &T);
while (T--)
{
scanf("%d%d", &n, &m);
mapinit();
int x, y;
for (int i = 1; i <= m; ++i)
{
scanf("%d%d", &x, &y);
insert(x, y);
}
solve();
memset(map, false, sizeof(map));
for (int i = 1; i <= n; ++i)
for (int j = p[i]; j != -1; j = e[j].next)
if (belong[i] != belong[e[j].v]) map[belong[i]][belong[e[j].v]] = true;
n = bcnt;
mapinit();
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
if (map[i][j]) insert(i, j);
//print_map();
printf("%d\n", n - calc());
}
return 0;
}
P1004
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#define EPS 0.00000001
using namespace std;
int n;
double ag;
int main()
{
int t;
double dir;
bool ok;
double maxg,ming;
scanf("%d",&t);
while(t--)
{
maxg = ming = 0.0;
dir = 0.0;ok = false;
scanf("%d",&n);
for (int i = 1; i <= n; ++i)
{
scanf("%lf",&ag);
while(ag > 180) ag -= 360;
while((ag + 180) <= EPS) ag += 360;
dir += ag;
maxg = max(maxg ,dir);
ming = min(ming ,dir);
//cout<<maxg<<"__"<<ming<<endl;
if (maxg - ming > 180)
ok = true;
}
if (n == 1 && fabs(maxg - ming - 180) < EPS)
ok = true;
if(ok)
printf("Yes\n");
else printf("No\n");
}
return 0;
}
#include <iostream>
using namespace std;
int n;
int main()
{
while (cin >> n)
{
if (n < 0) break;
cout << "I bet on Oregon Maple~" << endl;
}
return 0;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib> //有随机函数
using namespace std;
//pollard_rho返回一个因子,不能测质数
int list[9] = {2,3,5,7,11,13,17,19,61};
__int64 mod_pro(__int64 x,__int64 y,__int64 n)
{
__int64 ret=0,tmp=x%n;
while(y)
{
if(y&0x1)if((ret+=tmp)>n)ret-=n;
if((tmp<<=1)>n)tmp-=n;
y>>=1;
}
return ret;
}
__int64 mod(__int64 a,__int64 b,__int64 c)
{
__int64 ret=1;
while(b)
{
if(b&0x1)ret=mod_pro(ret,a,c);
a=mod_pro(a,a,c);
b>>=1;
}
return ret;
}
__int64 GCD(__int64 a,__int64 b)
{
return b ? GCD(b,a % b) : a;
}
__int64 pollard_rho(__int64 n,int c)
{
__int64 x,y,d,i=1,k=2;
x=rand()%(n-1)+1;
y=x;
while(true)
{
++i;
x=(mod_pro(x,x,n)+c)%n;
d=GCD(y-x,n);
if (1<d&&d<n) return d;
if (x==y) return n;
if (i==k)
y=x,k<<=1;
}
}
bool is_prime(__int64 n)
{
if (n == 2) return true;
if ((n % 2 == 0) && (n > 2)) return false;
__int64 k=0,m,a,i;
int t = 0;
for(m=n-1;!(m&1);m>>=1,k++);
while(t < 9)
{
a=mod(list[t]%(n-2)+2,m,n);
if(a!=1)
{
for(i=0;i<k&&a!=n-1;i++)
a=mod_pro(a,a,n);
if(i>=k)return false;
}
t++;
}
return true;
}
__int64 first, res;
bool findFactor(__int64 n,int k)
{
if (n==1) return false;
if (is_prime(n))
{
if (n != first)
{
res = n;
return true;
}
return false;
}
__int64 p=n;
while(p>=n)
p=pollard_rho(p,k--);
if (findFactor(p,k)) return true;
if (findFactor(n/p,k)) return true;
return false;
}
int main()
{
__int64 n, a, b, c, ori;
while (cin >> n)
{
ori = n;
first = n;
if (findFactor(n, 17))
{
a = res;
if (a * a * a == n)
{
cout << a << " " << a * a << " " << n << endl;
continue;
}
n /= a;
if (is_prime(n) && (n != a))
{
if (a > n) swap (a, n);
cout << a << " " << n << " " << ori << endl;
continue;
}
}
cout << "is not a D_num" << endl;
}
return 0;
}
P1007
#include <iostream>
#include <cstdio>
#include <cstring>
#define N 21
#define M 16
using namespace std;
int n, m, p, q, dp[N][N][2], cal[N][N][4], dd[N][N][2], dat[N][N][M][M], match[N], p[N], eid = 0;
bool use[N];
struct edge
{
int v, next;
}e[N * N];
void mapinit()
{
memset(P, -1, sizeof(P));
eid = 0;
}
void insert(int x, int y)
{
e[eid].v = y;
e[eid].next = P[x];
P[x] = eid++;
}
bool hungary(int v)
{
for (int i = P[v]; i != -1; i = e[i].next)
{
int u = e[i].v;
if (!use[u])
{
use[u] = true;
int temp = match[u];
match[u] = v;
if (temp == 0 || hungary(temp)) return true;
match[u] = temp;
}
}
return false;
}
int calc()
{
memset(match, 0, sizeof(match));
int cnt = 0;
for (int i = 1; i <= m; i++)
{
memset(use, false, sizeof(use));
if (hungary(i)) cnt++;
}
return cnt;
}
void calc(int startx, int starty)
{
int r1 = 0, r2 = 0, r3;
mapinit();
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= m; ++j)
if (dat[startx][starty][i][j]) insert(i, j);
r3 = calc();
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= m; ++j)
if (dat[startx][starty][i][j])
{
r1++;
break;
}
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= m; ++j)
if (dat[startx][starty][j][i])
{
r2++;
break;
}
cal[startx][starty][0] = r1 * p;
cal[startx][starty][1] = r2 * p;
cal[startx][starty][2] = r3 * p + q;
}
void update(int &a, int b)
{
if (b < a) a = b;
}
int main()
{
while (~scanf("%d%d%d%d", &n, &m, &p, &q))
{
memset(dp, 0x7f, sizeof(dp));
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
{
for (int x = 1; x <= m; ++x)
for (int y = 1; y <= m; ++y)
scanf("%d", &dat[i][j][x][y]);
calc(i, j);
}
dp[1][1][0] = min(cal[1][1][0], cal[1][1][2]);
dp[1][1][1] = min(cal[1][1][1], cal[1][1][2]);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
{
if (i < n)
{
update(dp[i + 1][j][0], dp[i][j][0] + cal[i + 1][j][0]);
update(dp[i + 1][j][0], dp[i][j][0] + q + cal[i + 1][j][1] + q);
update(dp[i + 1][j][0], dp[i][j][0] + cal[i + 1][j][2] + q);
update(dp[i + 1][j][1], dp[i][j][0] + cal[i + 1][j][0] + q);
update(dp[i + 1][j][1], dp[i][j][0] + q + cal[i + 1][j][1]);
update(dp[i + 1][j][1], dp[i][j][0] + cal[i + 1][j][2]);
}
if (j < n)
{
update(dp[i][j + 1][0], dp[i][j][1] + q + cal[i][j + 1][0]);
update(dp[i][j + 1][0], dp[i][j][1] + cal[i][j + 1][1] + q);
update(dp[i][j + 1][0], dp[i][j][1] + cal[i][j + 1][2]);
update(dp[i][j + 1][1], dp[i][j][1] + q + cal[i][j + 1][0] + q);
update(dp[i][j + 1][1], dp[i][j][1] + cal[i][j + 1][1]);
update(dp[i][j + 1][1], dp[i][j][1] + cal[i][j + 1][2] + q);
}
}
printf("%d\n", min(dp[n][n][0], dp[n][n][1]));
}
return 0;
}
P1008
#include <iostream>
#include <cstdio>
#include <cstring>
#define N 10003
using namespace std;
typedef struct
{
int value, key, arr;
} node;
node a[N];
bool cmp1( node n1, node n2 )
{
if ( n1.value != n2.value )
return ( n1.value < n2.value );
else return ( n1.key > n2.key );
}
bool cmp2( node n1, node n2 )
{
return ( n1.key < n2.key );
}
int Min( int x, int y )
{
if ( x < y ) return x;
return y;
}
int main()
{
int T, n, m, sum;
scanf( "%d", &T );
while ( T-- )
{
scanf( "%d%d", &n, &m );
int sum = 0;
for ( int i = 0; i < m; ++i )
{
scanf( "%d", &a[i].value );
sum += a[i].value;
a[i].key = i;
}
if ( sum < n )
{
printf( "IMPOSSIBLE\n");
continue;
}
sum = n;
sort( a, a+m,cmp1 );
for ( int i = 0; i < m; ++i )
{
int d = Min( a[i].value, sum/(m-i));
sum -= d;
a[i].arr = d;
}
sort( a, a+m,cmp2 );
for ( int i = 0; i < m-1; ++i )
printf( "%d ", a[i].arr, a[i].key, a[i].value );
printf( "%d\n", a[m-1].arr );
}
}
P1010
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define EPS 0.00000001
#define INF 999999999
using namespace std;
struct Point
{
double x,y;
}a[20005];
int n;
int cmp(const struct Point &s,const struct Point &t) //sortº¯Êý
{
if((t.x - s.x) >= EPS)
return 1;
else if(fabs(s.x - t.x) < EPS)
{
if((t.y - s.y) >= EPS)
return 1;
else return 0;
}else return 0;
}
double dis(int i,int j)
{
return sqrt((a[i].x - a[j].x)*(a[i].x - a[j].x) + (a[i].y - a[j].y)*(a[i].y - a[j].y));
}
double cross(Point p0,Point p1,Point p2)
{
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double cal(int l,int r)
{
if(l == r)
return INF;
if(l + 1 == r)
return INF;
if(l + 2 == r)
{
return (dis(l,r) + dis(l,l + 1) + dis(l + 1,r));
}
int mid = (l + r)/2;
double ans = INF;
ans = min(ans,min(cal(l,mid),cal(mid + 1,r)));
for(int i = mid; i >= l; --i)
{
if((fabs(a[i].x - a[mid].x) - ans) > INF)
break;
for (int j = i - 1; j >= l && j >= i - 5; --j)
{
double d = dis(i,j);
if((fabs(d - ans) > INF))
break;
for(int k = mid + 1; k <= r && k <= mid + 5; ++k)
{
ans = min(ans,d + dis(j,k) + dis(i,k));
}
}
for (int j = mid + 1; j <= r && j <= mid + 5; ++j)
{
double d = dis(i,j);
if((fabs(d - ans) > INF))
break;
for(int k = j + 1; k <= r && k <= j + 5; ++k)
{
ans = min(ans,d + dis(j,k) + dis(i,k));
}
}
}
return ans;
}
int main()
{
int T;
scanf("%d",&T);
while( T-- )
{
scanf("%d",&n);
for (int i = 1; i <= n; ++i)
scanf("%lf%lf",&a[i].x,&a[i].y);
sort(a + 1, a + n + 1,cmp);
printf("%.3f\n",cal(1,n));
}
return 0;
}