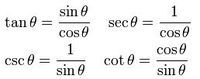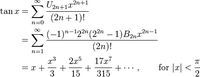数学 三角函数
编辑本段定义
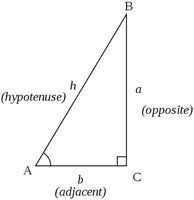
如右图,当平面上的三点A、B、C的连线,AB、AC、BC,构成一个直角三角形,其中∠ACB为直角。对于AB与AC的夹角∠BAC而言:
对边(opposite)a=BC 斜边(hypotenuse)h=AB 邻边(adjacent)b=AC
| 基本函数 | 英文 | 缩写 | 表达式 | 语言描述 |
| 正弦函数 | Sine | sin | a/h | ∠A的对边比斜边 |
| 余弦函数 | cosine | cos | b/h | ∠A的邻边比斜边 |
| 正切函数 | Tangent | tan | a/b | ∠A的对边比邻边 |
| 余切函数 | Cotangent | cot | b/a | ∠A的邻边比对边 |
| 正割函数 | Secant | sec | h/b | ∠A的斜边比邻边 |
| 余割函数 | Cosecant | csc | h/a | ∠A的斜边比对边 |
注:tan、cot曾被写作tg、ctg,现已不用这种写法。
罕见三角函数
除了上述六个常见的函数,还有一些不常见的三角函数:
| 函数名 | 与常见函数转化关系 |
| 正矢函数 | versinθ=1-cosθ |
| vercosinθ=1+cosθ | |
| 余矢函数 | coversinθ=1-sinθ |
| covercosinθ=1+sinθ | |
| 半正矢函数 | haversinθ=(1-cosθ)/2 |
| havercosinθ=(1+cosθ)/2 | |
| 半余矢函数 | hacoversinθ=(1-sinθ)/2 |
| hacovercosinθ=(1+sinθ)/2 | |
| 外正割函数 | exsecθ=secθ-1 |
| 外余割函数 | excscθ=cscθ-1 |
单位圆定义
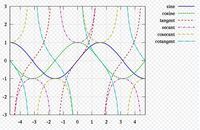
六个三角函数也可以依据半径为1中心为原点的单位圆来定义。单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和 π/2 弧度之间的角。它也提供了一个图像,把所有重要的三角函数都包含了。根据勾股定理,
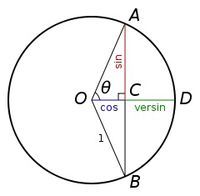
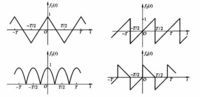
单位圆的方程是:x^2+y^2=1 图像中给出了用弧度度量的一些常见的角。逆时针方向的度量是正角,而顺时针的度量是负角。设一个过原点的线,同 x轴正半部分得到一个角 θ,并与单位圆相交。这个交点的 x和 y坐标分别等于cosθ和sinθ。图像中的三角形确保了这个公式;半径等于斜边且长度为1,所以有 sinθ= y/1 和 cosθ= x/1。单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于 1的一种查看无限个三角形的方式。 对于大于 2π 或小于等于2π 的角度,可直接继续绕单位圆旋转。在这种方式下,正弦和余弦变成了周期为 2π的周期函数:对于任何角度 θ和任何整数k。 周期函数的最小正周期叫做这个函数的“基本周期”。正弦、余弦、正割或余割的基本周期是全圆,也就是 2π 弧度或 360°;正切或余切的基本周期是半圆,也就是 π 弧度或 180°。上面只有正弦和余弦是直接使用单位圆定义的,其他四个三角函数的定义如图所示。
在正切函数的图像中,在角 kπ 附近变化缓慢,而在接近角 (k+ 1/2)π 的时候变化迅速。正切函数的图像在 θ = (k+ 1/2)π 有垂直渐近线。这是因为在 θ 从左侧接进 (k+ 1/2)π 的时候函数接近正无穷,而从右侧接近 (k+ 1/2)π 的时候函数接近负无穷。
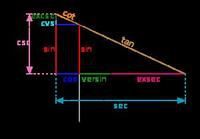
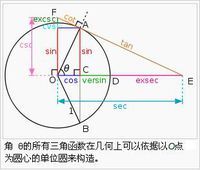
另一方面,所有基本三角函数都可依据中心为 O的单位圆来定义,类似于历史上使用的几何定义。特别 是,对于这个圆的弦AB,这里的 θ 是对向角的一半,sin θ是 AC(半弦),这是印度的阿耶波多介入的定义。cosθ 是水平距离 OC,versin θ=1-cosθ是CD。tanθ是通过 A的切线的线段AE的长度,所以这个函数才叫正切。cotθ是另一个切线段 AF。 secθ=OE和 cscθ=OF是割线(与圆相交于两点)的线段,所以可以看作 OA沿着 A 的切线分别向水平和垂直轴的投影。DE是 exsecθ= secθ-1(正割在圆外的部分)。通过这些构造,容易看出正割和正切函数在 θ 接近 π/2的时候发散,而余割和余切在 θ 接近零的时候发散。
编辑本段级数定义
只使用几何和极限的性质,可以证明正弦的导数是余弦,余弦的导数是负的正弦。(在微积分中,所有角度都以弧度来度量)。我们可以接着使用泰勒级数的理论来证明下列恒等式对于所有实数x都成立:
这些恒等式经常被用做正弦和余弦函数的定义。它们经常被用做三角函数的严格处理和应用的起点(比如,在傅里叶级数中),因为无穷级数的理论可从实数系的基础上发展而来,不需要任何几何方面的考虑。这样,这些函数的可微性和连续性便可以单独从级数定义来确立。 其他级数可见于:
注:Un是n次上/下数, Bn是n次伯努利数,
编辑本段三角函数线
依据单位圆定义,我们可以做三个有向线段(向量)来表示正弦、余弦、正切的值。 如图所示,圆O是一个单位圆,P是α的终边与单位圆上的交点,M点是P在x轴的投影,S(1,0)是圆O与x轴正半轴的交点,过S点做圆O的切线l。 那么向量MP对应的就是α的正弦值,向量OM对应的就是余弦值。OP的延长线(或反向延长线)与l的交点为T,则向量ST对应的就是正切值。向量的起止点不能颠倒,因为其方向是有意义的。 借助线三角函数线,我们可以观察到第二象限角α的正弦值为正,余弦值为负,正切值为负。 1.锐角三角函数定义 锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),(余割csc)都叫做角A的锐角三角函数。 正弦(sin)等于对边比斜边; 余弦(cos)等于邻边比斜边; 正切(tan)等于对边比邻边; 余切(cot)等于邻边比对边; 正割(sec)等于斜边比邻边; 余割(csc)等于斜边比对边。 2.互余角的三角函数关系 sin(90°-α)=cosα, cos(90°-α)=sinα, tan(90°-α)=cotα, cot(90°-α)=tanα。 3.同角三角函数间的关系 商数关系: sinA/cosA=tanA ·平方关系: sin^2(A)+cos^2(A)=1 ·积的关系: sinA=tanA·cosA cosA=cotA·sinA cotA=cosA·cscA tanA·cotA=1 ·倒数关系: 直角三角形ABC中 角A的正弦值就等于角A的对边比斜边, 余弦等于角A的邻边比斜边 正切等于对边比邻边, 余切等于邻边比对边 4.三角函数值 (1)特殊角三角函数值 (2)0°~90°的任意角的三角函数值,查三角函数表 (3)锐角三角函数值的变化情况 (i)锐角三角函数值都是正值 (ii)当角度在0°~90°间变化时, 正弦值随着角度的增大(或减小)而增大(或减小) 余弦值随着角度的增大(或减小)而减小(或增大) 正切值随着角度的增大(或减小)而增大(或减小) 余切值随着角度的增大(或减小)而减小(或增大) (iii)当角度在0°≤∠A≤90°间变化时, 0≤sinα≤1, 1≥cosA≥0 当角度在0°<∠A<90°间变化时, tanA>0, cotA>0 特殊的三角函数值
| A | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° |
| A弧度 | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 |
| sinA | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 |
| cosA | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | 0 |
| tanA | 0 | √3/3 | 1 | √3 | None | -√3 | -1 | -√3/3 | 0 | None |
| cotA | None | √3 | 1 | √3/3 | 0 | -√3/3 | -1 | -√3 | None | 0 |
| A | 15° | 75° |
| A弧度 | π/12 | 5π/12 |
| sinA | √6-√2/4 | √6+√2/4 |
| cosA | √6+√2/4 | √6-√2/4 |
| tanA | 2-√3 | 2+√3 |
| cotA | 2+√3 | 2-√3 |
“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的 重要内容。从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。在义务教育第三学段,主要研 究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。在高中阶段的三角内容是三角学的主体部分,包括解斜三角 形、三角函数、反三角函数和简单的三角方程。无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
编辑本段起源
“三角学”,英文Trigonometry,法文Trigonometrie,德文Trigonometrie,都来自拉丁文 Trigonometria。 现代三角学一词最初见于希腊文。最先使用Trigonometry这个词的是皮蒂斯楚斯( Bartholomeo Pitiscus,1516-1613),他在1595年出版一本著作《三角学:解三角学的简明处理》,创造了这个新词。它是由τριγωυου(三角 学)及μετρει υ(测量)两字构成的,原意为三角形的测量,或者说解三角形。古希腊文里没有这个字,原因是当时三角学还没有形成一门独立的科学,而是依附于天文学。因此 解三角形构成了古代三角学的实用基础。 早期的解三角形是因天文观测的需要而引起的。还在很早的时候,由于垦殖和畜牧的需要,人们就开 始作长途迁移;后来,贸易的发展和求知的欲望,又推动他们去长途旅行。在当时,这种迁移和旅行是一种冒险的行动。人们穿越无边无际、荒无人烟的草地和原始 森林,或者经水路沿着海岸线作长途航行,无论是那种方式,都首先要明确方向。那时,人们白天拿太阳作路标,夜里则以星星为指路灯。太阳和星星给长期跋山涉 水的商队指出了正确的道路,也给那些沿着遥远的异域海岸航行的人指出了正确的道路。 就这样,最初的以太阳和星星为目标的天文观测,以及为这种观测服务的原始的三角测量就应运而生了。因此可以说,三角学是紧密地同天文学相联系而迈出自己发展史的第一步的。
三角学问题的提出
三角学理论的基础,是对三角形各元素之 间相依关系的认识。一般认为,这一认识最早是由希腊天文学家获得的。当时,希腊天文学家为了正确地测量天体的位置。研究天体的运行轨道,力求把天文学发展 成为一门以精确的观测和正确的计算为基础之具有定量分析的科学。他们给自己提出的第一个任务是解直角三角形,因为进行天文观测时,人与星球以及大地的位置 关系,通常是以直角三角形边角之间的关系反映出来的。在很早以前,希腊天文学家从天文观测的经验中获得了这样一个认识:星球距地面的高度是可以通过人观测 星球时所采用的角度来反映的(如图一);角度(∠ABC)越大,星球距地面(AC)就越高。然而,星球的高度与人观测的角度之间在数量上究竟怎么样呢?能 不能把各种不同的角度所反映的星球的高度都一一算出来呢?这就是天文学向数学提出的第一个课题-制造弦表。所谓弦表,就是在保持AB不变的情况下可以供查 阅的表 (如图二),AC的长度与∠ABC的大小之间的对应关系。
独立三角学的产生
虽然后期的阿拉伯数学家已经开始对三角学进行专门的整理和研究,他们的工作也可以算作是使三角学从天文学中独立出来的表现,但是严格地说,他们并没有创立起一门独立的三角学。真正把三角学作为数学的一个独立学科加以系统叙述的,是德国数学家雷基奥蒙坦纳斯。 雷基奥蒙坦纳斯是十五世纪最有声望的德国数学家约翰●谬勒的笔名。他生于哥尼斯堡,年轻时就积极从事欧洲文艺复兴时期作品的收集和翻译工作,并热心出版古希腊和阿拉伯著作。因此对阿拉伯数学家们在三角方面的工作比较了解。
1464年,他以雷基奥蒙坦纳斯的名字发表了《论各种三角形》。在书中,他把以往散见在各种书上的三角学知识,系统地综合了起来,成了三角学在数学上的一个分支。
现代三角学的确认
直到十八世纪,所有的三角量:正弦、余弦、正切、余切、正割和余割,都始终被认为是已知圆内与同一条弧有关的某些线段,即三角学是以几何的面貌表现出来 的,这也可以说是三角学的古典面貌。三角学的现代特征,是把三角量看作为函数,即看作为是一种与角相对应的函数值。这方面的工作是由欧拉作 出的。1748年,尤拉发表著名的《无穷小分析引论》一书,指出:”三角函数是一种函数线与圆半径的比值”。具体地说,任意一个角的三角函数,都可以认为 是以这个角的顶点为圆心,以某定长为半径作圆,由角的一边与圆周的交点P向另一边作垂线PM后,所得的线段OP、OM、MP(即函数线)相互之间所取的比 值(如图八),sinα=MP/OP,cosα=OM/OP,tanα= MP/OM等。若令半径为单位长,那么所有的六个三角函数又可大为简化。 尤拉的这个定义是极其科学的,它使三角学从静态地只是研究三角形解法的狭隘天地中解脱了出来,使它有可能去反映运动和变化的过程,从而使三角学成为一门具有现代特征的分析性学科。正如欧拉所说,引进三角函数以后,原来意义下的正弦等三角量,都可以脱离几何图形去进行自由的运算。一切三角关系式也将很容易地从三角函数的定义出发直接得出。这样,就使得从希帕克起许多数学家为之奋斗而得出的三角关系式,有了坚实的理论依据,而且大大地丰富了。严格地说,这时才是三角学的真正确立。
“正弦”的由来
公元五世纪到十二世纪,印度数学家对三角学作出了较大的贡献。尽管当时三角学仍然还是天文学的一个计算工具,是一个附属品,但是三角学的内容却由于印度数学家的努力而大大的丰富了。 三角学中”正弦”和”余弦”的概念就是由印度数学家首先引进的,他们还造出了比托勒密更精确的正弦表。
我们已知道,托勒密和希帕克造出的弦表是圆的全弦表,它是把圆弧同弧所夹的弦对应起来的。印度数学家不同,他们把半弦(AC)与全弦所对弧的一半(AD)相对应,即将AC与∠AOC对应(如图五 ),这样,他们造出的就不再是”全弦表”,而是”正弦表”了。 印度人称连结弧(AB)的两端的弦(AB)为”吉瓦”,是弓弦的意思;称AB的一半(AC) 为”阿尔哈吉瓦”。后来”吉瓦”这个词译成阿拉伯文时被误解为”弯曲”、”凹处”,阿拉伯语是 ”dschaib”。十二世纪,阿拉伯文被转译成拉丁文,这个字被意译成了”sinus”。 三角学输入我国,开始于明崇祯4年(1631年),这一年,邓玉函、汤若望和徐光启合编《大测》,作为历书的一部份呈献给朝廷,这是我国第一部编译的三角学。在《大测》中,首先将sinus译为”正半弦”,简称”正弦”,这就成了正弦一词的由来。
“弦表”问世
根据现在的认识,弦表的制作似应该是由一系列不同的角出发,去作一系列直角三角形,然后一一量出AC,A’C’,A’’C’’…之间的距离。然而,第一 张弦表制作者希腊文学家希帕克 (Hipparchus,约前180~前125)不是这样作,他采用的是在同一个固定的圆内,去计算给定度数的圆弧AB所对应的弦AB的长(如图三)。这 就是说,希帕克是靠计算,而不是靠工具量出弦长来制表的,这正是他的卓越之处。希帕克的原著早已失传,现在我们所知关于希帕克在三角学上的成就,是从公元 二世纪希腊著名天文学家托勒密的遗著《天文集》中得到的。虽然托勒密说他的这些成就出自希帕克,但事实上不少是他自己的创造。 据托勒密书中记载,为了度量圆弧与弦长,他们采用了巴比伦人的60进位法。把圆周360等分, 把它的半径60等分,在圆周和半径的每一等分中再等分60份,每一小份又等分为60份,这样就得出了托勒密所谓的第一小份和第二小份。很久以后,罗马人把 它们分别取名为”partes minutae primae”和”partes minutae secundae”;后来,这两个名字演变为”minute”和”second”,成为现在角和时间的度 量上”分”和”秒”这两个单位得起源。 建立了半径与圆周的度量单位以后,希帕克和托勒密先着手计算一些特殊圆弧所对应的弦长。比如 60°弧(1/6圆周长)所对的弦长,正好是内接正六边形的边长,它与半径相等,因此得出60°弧对应的弦值是60个半径单位(半径长的1/60为一个单位);用同样的方法,可以算出120°弧、90°弧以及72°弧所对应的弦值(如图四)。有了这些弧所对应的弦值,接着就利用现在所称的”托勒密定理”,来推算两条已知所对弦长的弧的”和”与”差”所对的弦长,以及由一条弧所对的弦长来计算这条弧的一半所对的弦长。正是基于这样一种几何上的推算。他们终于造出了世界上第一张弦表。
60进制
60进制以度为单位,将圆周分成360等份,每一份所对的圆心角叫做1度,1度等于60分,1分等于60秒。在时间上,1小时有60分,1分有60秒。这种60进制起源于巴比伦是1854年由欣克斯(Edward Hincks,1792-1866) 研究泥板上的楔形文字所发现的,这些泥板是公元前2300-1600年的遗物。Edward Hincks 是爱尔兰人,以解读埃及的象形文字及巴比伦的楔形文字著称于世。 巴比伦人为什么用60作为进位的基数呢?这是很有趣的问题,引起后人的种种猜测。以下我就列举几个有趣的例子。 (1)数学史家M.康托尔(Moritz Benedikt Cantor,1829-1920)曾认为他们最初以360天为一年。将圆周分为360度,太阳就每天行一度。又圆内恰好可以连续作6条等于半径长的弦, 每一条弦所对的长是60度,基数60或者由此而来。但根据考证,巴比伦人很早就知道太阳年是365日,太阴年(12个月)是354或355日,因此这种假 说很难成立。康托尔后来也放弃了这种说法。 (2)60这个数字的选择是因为它是许多简单数字2,3,4,5,6,10,12,……的倍数,从而它的1/2,1/3,1/4, 1/5,……都是整数,用起来比较方便。这种想法早在希腊时代的赛翁就已指出,近年来又有 勒夫勒等人提倡。然而有人认为这是违反历史事实的,因为记数制度不可能由某些学者为了”科学目的”自由创造出来,而是悠久历史发展的结果。 (3)克维奇(G.Kewitsch)在1904年提出,当时两河流域有两个民族,1个用10 进制,一个用6进制。两种制度混合调和就形成60进制。10进制是容易理解的,因为人们用10个指头来计算,而6进制是用一只手来计算,5个指头表示1至 5,握拳表示6,6以上,就要进位了。其实有几种意见认为是和指算有关。用手指计算的确在某些地区和年代流行过,甚至在近代也是如此。像我国也有”掐指一 算”的说法。 总之,对于基数60的起源,至今还没有一致公认的看法。中国在殷商时代(公元前16-11世纪),就开始用干支纪日、纪年,从甲子起,60一个循环,周而复始,叫做六十花甲子。可以说和巴比伦异曲同工,不过没有发展为进位值。 *希伯诸斯据说曾编著了第一个三角函数表,这个成就使他赢得了“三角学之父”的称谓。
编辑本段特殊角的三角函数
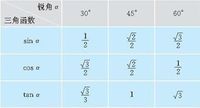
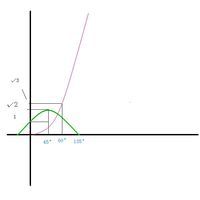
在三角函数中,有一些特殊角,例如30°、45°、60°,这些角的三角函数值为简单单项式,计算中可以直接求出具体的值。 这些函数的值参见右图:
同角三角函数关系式
| 平方关系 | sin^2(α)+cos^2(α)=1 cos(2α)=cos^2(α)-sin^2(α)=1- 2sin^2(α)=2cos^2(α)-1 sin(2α)=2sin(α)cos(α) tan^2(α)+1=1/cos^2(α) 2sin^2(α)=1-cos(4α) cot^2(α)+1=1/sin^2(α) |
| 积的关系 | sinα=tanα×cosα cosα=cotα×sinα tanα=sinα×secα cotα=cosα×cscα secα=tanα×cscα cscα=secα×cotα |
| 倒数关系 | tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 |
| 商的关系 | sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα |
·对称性 180度-α的终边和α的终边关于y轴对称。 -α的终边和α的终边关于x轴对称。 180度+α的终边和α的终边关于原点对称。 90度-α的终边和α的终边关于y=x对称。
诱导公式
| 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等 k是整数 |
sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα sec(2kπ+α)=secα csc(2kπ+α)=cscα |
| 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系 |
sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα sec(π+α)=-secα csc(π+α)=-cscα |
| 公式三: 任意角α与 -α的三角函数值之间的关系 |
sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα sec(-α)=secα csc(-α)=-cscα |
| 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系 |
sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα sec(π-α)=-secα csc(π-α)=cscα |
| 公式五: 利用公式四和三角函数的奇偶性可以得到α-π与α的三角函数值之间的关系 |
sin(α-π)=-sinα cos(α-π)=-cosα tan(α-π)=tanα cot(α-π)=cotα sec(α-π)=-secα csc(α-π)=-cscα |
| 公式六: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系 |
sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα sec(2π-α)=secα csc(2π-α)=-cscα |
| 公式七: π/2±α及3π/2±α与α的三角函数值之间的关系 |
sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sec(π/2+α)=-cscα csc(π/2+α)=secα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sec(π/2-α)=cscα csc(π/2-α)=secα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sec(3π/2+α)=cscα csc(3π/2+α)=-secα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα sec(3π/2-α)=-cscα csc(3π/2-α)=-secα |
诱导公式的表格以及推导方法(定名法则和定号法则)
| sinα | cosα | tanα | cotα | secα | cscα | |
| 2kπ+α | sinα | cosα | tanα | cotα | secα | cscα |
| (1/2)kπ-α | cosα | sinα | cotα | tanα | cscα | secα |
| (1/2)kπ+α | cosα | -sinα | -cotα | -tanα | -cscα | secα |
| kπ-α | sinα | -cosα | -tanα | -cotα | -secα | cscα |
| kπ+α | -sinα | -cosα | tanα | cotα | -secα | -cscα |
| (3/2)kπ-α | -cosα | -sinα | cotα | tanα | -cscα | -secα |
| (3/2)kπ+α | -cosα | sinα | -cotα | -tanα | cscα | -secα |
| 2kπ-α | -sinα | cosα | -tanα | -cotα | secα | -cscα |
| ﹣α | -sinα | cosα | -tanα | -cotα | secα | -cscα |
定名法则 90°的奇数倍+α的三角函数,其绝对值与α三角函数的绝对值互为余函数。90°的偶数倍+α的三角函数与α的三角函数绝对值相同。也就是“奇余偶同,奇变偶不变”。 定号法则 将α看做锐角(注意是“看做”),按所得的角的象限,取三角函数的符号。也就是“象限定号,符号看象限”。(或为“奇变偶不变,符号看象限”)。 在Kπ/2中如果K为偶数时函数名不变,若为奇数时函数名变为相反的函数名。正负号看原函数中α所在象限的正负号。关于正负号有可口诀;一全正二正弦,三正切四余弦,即第一象限全部为正,第二象限角正弦为正,第三为正切、余切为正,第四象限余弦为正。)还可简记为:sin上cos右tan对角,即sin的正值都在x轴上方,cos的正值都在y轴右方,tan的正值斜着。 比如:90°+α。定名:90°是90°的奇数倍,所以应取余函数;定号:将α看做锐角,那么90°+α是第二象限角,第二象限角的正弦为正,余弦为负。所以sin(90°+α)=cosα , cos(90°+α)=-sinα 这个非常神奇,屡试不爽~ 还有一个口诀“纵变横不变,符号看象限”,例如:sin(90°+α),90°的终边在纵轴上,所以函数名变为相反的函数名,即cos,将α看做锐角,那么90°+α是第二象限角,第二象限角的正弦为正,所以sin(90°+α)=cosα。
对称轴与对称中心
y=sinx 对称轴:x=kπ+π/2(k∈z) 对称中心:(kπ,0)(k∈z) y=cosx 对称轴:x=kπ(k∈z) 对称中心:(kπ+π/2,0)(k∈z) y=tanx 对称轴:无 对称中心:(kπ,0)(k∈z)
两角和与差的三角函数
cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβ sin(α±β)=sinα·cosβ±cosα·sinβ tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
和差化积公式
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
积化和差公式
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)] cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)] cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)] sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
倍角公式
sin(2α)=2sinα·cosα=2/(tanα+cotα) cos(2α)=cos^2α-sin^2;α=2cos^2;α-1=1-2sin^2;α tan(2α)=2tanα/(1-tan^2;α) cot(2α)=(cot^2;α-1)/(2cotα) sec(2α)=sec^2;α/(1-tan^2;α) csc(2α)=1/2*secα·cscα
三倍角公式
sin(3α) = 3sinα-4sin^3;α = 4sinα·sin(60°+α)sin(60°-α) cos(3α) = 4cos^3;α-3cosα = 4cosα·cos(60°+α)cos(60°-α) tan(3α) = (3tanα-tan^3;α)/(1-3tan^2;α) = tanαtan(π/3+α)tan(π/3-α) cot(3α)=(cot^3;α-3cotα)/(3cotα-1)
n倍角公式
sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-… cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…
半角公式
sin(α/2)=±√((1-cosα)/2) cos(α/2)=±√((1+cosα)/2) tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα cot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα) sec(α/2)=±√((2secα/(secα+1)) csc(α/2)=±√((2secα/(secα-1))
辅助角公式
Asinα+Bcosα=√(A^2;+B^2;)sin(α+arctan(B/A)) Asinα+Bcosα=√(A^2;+B^2;)cos(α-arctan(A/B))
万能公式
sin(a)= (2tan(a/2))/(1+tan^2;(a/2)) cos(a)= (1-tan^2;(a/2))/(1+tan^2;(a/2)) tan(a)= (2tan(a/2))/(1-tan^2;(a/2))
降幂公式
sin^2;α=(1-cos(2α))/2=versin(2α)/2 cos^2;α=(1+cos(2α))/2=covers(2α)/2 tan^2;α=(1-cos(2α))/(1+cos(2α))
三角和的三角函数
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)
特殊角的三角函数值
| 正弦 | 余弦 | 正切 | 余切 | ||
| 0 | 0 | 1 | 0 | 不存在 | |
| π/6 | 1/2 | √3/2 | √3/3 | √3 | |
| π/4 | √2/2 | √2/2 | 1 | 1 | |
| π/3 | √3/2 | 1/2 | √3 | √3/3 | |
| π/2 | 1 | 0 | 不存在 | 0 | |
| π | 0 | -1 | 0 | 不存在 |
幂级数
c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞) c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞) 它们的各项都是正整数幂的幂函数, 其中c0,c1,c2,...cn...及a都是常数, 这种级数称为幂级数。
泰勒展开式
泰勒展开式又叫幂级数展开法 f(x)=f(a)+f'(a)/1!*(x-a)+f''(a)/2!*(x-a)2+...+f(n)(a)/n!*(x-a)n+…… 实用幂级数: e^x = 1+x+x^2/2!+x^3/3!+……+x^n/n!+…… ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1) sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。 (-∞<x<∞) cos x = 1-x^2/2!+x^4/4!-……+(-1)k*(x^(2k))/(2k)!+…… (-∞<x<∞) arcsin x = x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + ……(|x|<1) arccos x = π - ( x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + …… ) (|x|<1) arctan x = x - x^3/3 + x^5/5 -……(x≤1) sinh x = x+x^3/3!+x^5/5!+……+(-1)^(k-1)*(x^2k-1)/(2k-1)!+…… (-∞<x<∞) cosh x = 1+x^2/2!+x^4/4!+……+(-1)k*(x^2k)/(2k)!+……(-∞<x<∞) arcsinh x = x - 1/2*x^3/3 + 1*3/(2*4)*x^5/5 - …… (|x|<1) arctanh x = x + x^3/3 + x^5/5 + ……(|x|<1) 在解初等三角函数时,只需记住公式便可轻松作答,在竞赛中,往往会用到与图像结合的方法求三角函数值、三角函数不等式、面积等等。
傅立叶级数
傅里叶级数又称三角级数 f(x)=a0/2+∑(n=0..∞) (ancosnx+bnsinnx) a0=1/π∫(π..-π) (f(x))dx an=1/π∫(π..-π) (f(x)cosnx)dx bn=1/π∫(π..-π) (f(x)sinnx)dx
三角函数的数值符号
正弦:第一,二象限为正,第三,四象限为负 余弦:第一,四象限为正,第二,三象限为负 正切:第一,三象限为正,第二,四象限为负
编辑本段相关概念
三角形与三角函数
1、正弦定理:在三角形中,各边和它所对的角的正弦的比相等,即a/sinA=b/sinB=c/sinC=2R .(其中R为外接圆的半径) 2、第一余弦定理:三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和,即a=c cosB + b cosC 3、第二余弦定理:三角形中任何一边的平方等于其它两边的平方之和减去这两边与它们夹角的余弦的积的2倍,即a^2=b^2+c^2-2bc·cosA 4、正切定理(napier比拟):三角形中任意两边差和的比值等于对应角半角差和的正切比值,即(a-b)/(a+b)=tan[(A-B)/2]/tan[(A+B)/2]=tan[(A-B)/2]/cot(C/2) 5、三角形中的恒等式: 对于任意非直角三角形中,如三角形ABC,总有tanA+tanB+tanC=tanAtanBtanC 证明: 已知(A+B)=(π-C) 所以tan(A+B)=tan(π-C) 则(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC) 整理可得 tanA+tanB+tanC=tanAtanBtanC 类似地,我们同样也可以求证:当α+β+γ=nπ(n∈Z)时,总有tanα+tanβ+tanγ=tanαtanβtanγ 三角函数图像:
定义域和值域
sin(x),cos(x)的定义域为R,值域为〔-1,1〕 tan(x)的定义域为x不等于π/2+kπ,值域为R cot(x)的定义域为x不等于kπ,值域为R y=a·sin(x)+b·cos(x)+c 的值域为 [ c-√(a²+b²) , c+√(a²+b²)]
三角函数的画法
以y=sinx的图像为例,得到y=Asin(ωx+φ)的图像: 方法一: y=sinx→【左移(φ>0)/右移(φ<0) ∣∣∣φ∣个单位】 →y=sin(x+φ)→【纵坐标不变,横坐标伸缩到原来的(1/ω)】→y=sin(ωx+φ) →【纵坐标变为原来的A倍(伸长[A>1] / 缩短[0<A<1])】→ y=Asin(ωx+φ) 方法二: y=sinx→【纵坐标不变,横坐标伸缩到原来的(1/ω)】→y=sinωx→【左移(φ& gt;0)/右移(φ<0)∣φ∣/ω 个单位】→y=sin(ωx+φ) →【纵坐标变为原来的A倍(伸长[A>1] / 缩短[0<A<1])】→ y=Asin(ωx+φ)
初等三角函数导数
y=sinx---y'=cosx y=cosx---y'=-sinx y=tanx---y'=1/cos^2x =sec^2x y=cotx---y'= -1/sin^2x= - csc^2x y=secx---y'=secxtanx y=cscx---y'=-cscxcotx y=arcsinx---y'=1/√(1-x²) y=arccosx---y'= -1/√(1-x²) y=arctanx---y'=1/(1+x²) y=arccotx---y'= -1/(1+x²) 备注:此处² 是对前式进行平方:x² 也即 x^2
倍半角规律
如果角a的余弦值为1/2,那么a/2的余弦值为√3/2
反三角函数
三角函数的反函数,是多值函数。它们是反正弦Arcsin x,反余弦Arccos x,反正切Arctan x,反余切Arccot x等,各自表示其正弦、余弦、正切、余切、正割、余割为x的角。为限制反三角函数为单值函数,将反正弦函数的值y限在y=-π/2≤y≤π/2,将y为反正弦函数的主值,记为y=arcsin x;相应地,反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2<y<π/2;反余切函数y=arccot x的主值限在0<y<π。 反三角函数实际上并不能叫做函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数y=x对称。其概念首先由欧拉提出,并且首先使用了arc+函数名的形式表示反三角函数,而不是f-1(x). 反三角函数主要是三个: y=arcsin(x),定义域[-1,1],值域[-π/2,π/2],图象用红色线条; y=arccos(x),定义域[-1,1],值域[0,π],图象用蓝色线条; y=arctan(x),定义域(-∞,+∞),值域(-π/2,π/2),图象用绿色线条; sinarcsin(x)=x,定义域[-1,1],值域 [-π/2,π/2] 证明方法如下:设arcsin(x)=y,则sin(y)=x ,将这两个式子代入上式即可得 其他几个用类似方法可得。
编辑本段高等应用
总体情况
高等代数中三角函数的指数表示(由泰勒级数易得): sinz=[e^(iz)-e^(-iz)]/(2i) cosz=[e^(iz)+e^(-iz)]/2 tanx=[e^(iz)-e^(-iz)]/[ie^(iz)+ie^(-iz)] 泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+… ≦ 此时三角函数定义域已推广至整个复数集。 ·三角函数作为微分方程的解: 对于微分方程组 y=-y'';y=y'''',有通解Q,可证明 Q=Asinx+Bcosx,因此也可以从此出发定义三角函数。 补充:由相应的指数表示我们可以定义一种类似的函数--双曲函数,其拥有很多与三角函数的类似的性质,二者相映成趣。
复数域内性质
(1)对于z为实数y来说,复数域内正余弦函数的性质与通常所说的正余弦函数性质是一样的。 (2)复数域内正余弦函数在z平面是解析的。 (3)在复数域内不能再断言|sinz|≦1,|cosz|≦1。 (4)sinz、cosz分别为奇函数,偶函数,且以2π为周期。 (5) 棣莫佛(De Moivre)定理 设两个复数(用三角形式表示)Z1=r1(cosθ1+isinθ1) ,Z2=r2(cosθ2+isinθ2),则: Z1Z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].
编辑本段性质定理
三角函数,正如其名称那样,在三角学中是十分重要的,主要是因为下列两个结果。
正弦定理
对于边长为 a, b和 c而相应角为 A, B和 C的三角形,有: sinA / a = sinB / b = sinC/c 也可表示为: a/sinA=b/sinB=c/sinC=2R 变形:a=2RsinA,b=2RsinB,c=2RsinC 其中R是三角形的外接圆半径。 它可以通过把三角形分为两个直角三角形并使用上述正弦的定义来证明。在这个定理中出现的公共数 (sinA)/a是通过 A, B和 C三点的圆的直径的倒数。正弦定理用于在一个三角形中(1)已知两个角和一个边求未知边和角(2)已知两边及其一边的对角求其他角和边的问题。这是三角测量中常见情况。
余弦定理
对于边长为 a, b和 c而相应角为 A, B和 C的三角形,有: c^2=a^2+b^2-2ab·cosC. 也可表示为: cosC=(a^2+b^2-c^2)/ 2ab. 这个定理也可以通过把三角形分为两个直角三角形来证明。余弦定理用于在一个三角形的两个边和一个角已知时确定未知的数据。 如果这个角不是两条边的夹角,那么三角形可能不是唯一的(边-边-角)。要小心余弦定理的这种歧义情况。
正切定理
对于边长为 a, b和 c而相应角为 A, B和 C的三角形,有: (a+b)/(a-b) = tan[(A+B)/2]/tan[(A-B)/2]
编辑本段应用:一元三次方程
一元三次方程的解是三个不相等的实根时,可用三角函数知识求出方程的解。 一元三次方程aX^3+bX^2+cX+d=0,(a,b,c,d∈R,且a≠0) 重根判别式:A=b^2-3ac;B=bc-9ad;C=c^2-3bd。 总判别式:Δ=B^2-4AC。 当Δ=B^2-4AC<0时,盛金公式④: X⑴=(-b-2A^(1/2)cos(θ/3))/(3a) X(2,3)=(-b+A^(1/2)(cos(θ/3)±3^(1/2)sin(θ/3)))/(3a), 其中θ=arccosT,T=(2Ab-3aB)/(2A^(3/2)),(A>0,-1<T<1)。 在利用卡尔丹公式解三次方程时,对于x^3+px+q=0,有 x1=√(-p/3)cos(Φ/3) x2=√(-p/3)cos(Φ/3+2π/3) x3=√(-p/3)cos(Φ/3+4π/3) 对于一般的方程ax^3+bx^2+cx+d=0,只需令x=y-b/(3a)即可化为上式求解。 例:一建筑物的楼顶要建一个储水池,按施工的设计要求,这个储水池的长、宽、高之和为70.5dm(为了减少占用楼顶面积,取长>高>宽),满储水量为10082.44(dm)^3,立体对角线为1903.17dm,问:如何施工才能达到设计要求? 解:设取长、宽、高分别为X⑴、X⑵、X⑶,依题意: X⑴+X⑵+X⑶=70.5 X⑴·X⑵·X⑶=10082.44 X⑴^2+X⑵^2+X⑶^2=1903.17。 解这个方程组。 根据韦达定理,得一元三次方程: X^3-70.5X^2+1533.54X-10082.44=0 a=1,b=-70.5,c=1533.54,d=-10082.44。 A=369.63;B=-17372.61;C=219308.8716, Δ=-22444974.63<0。 根据盛金判别法,此方程有三个不相等的实根。 应用盛金公式④求解。 θ=90°。 把有关值代入盛金公式④,得: X⑴=12.4(dm);X⑵=34.6(dm);X⑶=23.5(dm)。 经检验,结果正确。 因为取长>高>宽, 所以,应取长为34.6dm;高为23.5dm;宽为12.4dm来进行施工。
编辑本段复数三角函数
sin(a+bi)=sinacosbi+sinbicosa =sinachb+ishbcosa cos(a-bi)=coscosbi+sinbisina =cosachb+ishbsina tan(a+bi)=sin(a+bi)/cos(a+bi) cot(a+bi)=cos(a+bi)/sin(a+bi) sec(a+bi)=1/cos(a+bi) csc(a+bi)=1/sin(a+bi)
编辑本段三角函数常见考法
本节知识在段考中是必考内容,多以选择题和填空题形式考查基础知识,多以解答题的形式考查三角函数的图像和性质。在高考中,多以解答题的形式和三角函数的概念、简单的三角恒等变换、解三角形联合考查三角函数的最值、单调区间、对称性等,属于难题。