Timus 1150. Digits

Timus 1150. Digits 要求计算 1 到 N 的正整数中包含 0 .. 9 的数目。

---

1150. Digits

Time Limit: 2.0 second
Memory Limit: 16 MB

John Smith has decided to number the pages in his notebook from 1 to N. Please, figure out the number of zeros, ones, twos, ... , nines he might need.

Input

One number N (N<1000000000)

Output

There should be 10 lines. The first line should contain the number of zeros needed , the second line should contain the number of ones needed, ... , the tenth line should contain the number of nines needed.

Sample

input	output
12	1 5 2 1 1 1 1 1 1 1

Problem Author: Eugene Bryzgalov
Problem Source: Ural Collegiate Programming Contest, April 2001, Perm, English Tour

---

解答如下：

 1  using  System;
 2 
 3  namespace  Skyiv.Ben.Timus
 4  {
 5     //  Timus 1150. Digits: 求 1 到 N 的正整数中包含 0 .. 9 的数目。
 6     //  N     9  99 999 9,999 99,999 999,999 9,999,999 99,999,999 999,999,999
 7     //  i*p   1  20 300 4,000 50,000 600,000 7,000,000 80,000,000 900,000,000
 8     //  q     1  11 111 1,111 11,111 111,111 1,111,111 11,111,111 111,111,111
 9     //  上表中，i*p 是 1 .. 9 的数目，i*p - q 是 0 的数目。
10     //   http://acm.timus.ru/problem.aspx?space=1 &num=1150
11     sealed   class  T1150
12    {
13       static   void  Main()
14      {
15         int [] a  =   new   int [ 10 ];  //  0 .. 9 的数目
16         int  k  =   0 , n  =   int .Parse(Console.ReadLine());
17         for  ( int  i  =   0 , m  =   1 , p  =   1 , q  =   0 ; n  >   0 ; i ++ , n  /=   10 , q  =  q  *   10   +   1 )
18        {
19           int  d  =  n  %   10 ;    //    d: n 的第 i 位数字，i: 0:个位 1:十位 2:百位 
20          k  +=  i  *  p  *  d;    //  i*p: 0 1 20 300 4000 50000 600000 7000000 
21           if  (i  >   0 ) p  *=   10 ;  //  p: 1 1 10 100 1000 10000 100000 1000000 
22           for  ( int  j  =  d  -   1 ; j  >=   0 ; j -- ) a[j]  +=  p;  //  0 .. d-1 的数目
23           if  (n < 10 ) a[ 0 ]  -=  p  +  q;  //  q: 0 1 11 111 1111 11111 111111 
24          a[d]  +=  m;   //  d 的数目
25          m  +=  d  *  p;  //  m: n 的低 i 位 + 1, 例 n: 59842，m: 1 3 43 843 9843
26        }
27         for  ( int  i  =   0 ; i  <  a.Length; i ++ ) Console.WriteLine(a[i]  +  k);
28      }
29    }
30  }

本程序使用的算法是非常高效的，时间复杂度是 O(logN)。主要难点是计算 0 的数目。今天断断续续用了三、四个小时才完全搞定这个算法。

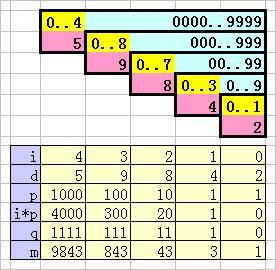
上图是输入 N = 59842 的示意图。在这个例子中，i 从 0 循环到 4，分别对应 N 的个、十、百、千、万位。在循环体内，又分为三个部分进行计数。下面以 i = 2，即 N 的百位数 d = 8 为例进行说明：

• 程序中的第 20 行:  k += i * p * d;  对应上图中的浅青色部分 ( 个位没有浅青色部分，其计数为零 )。i * p = 20，表示 00 .. 99 范围内每种数字各出现 20 次。d = 8，表示 0 .. 7 共有 8 种 ( 上图中黄色部分 )，所以总计数为 i * p * d。
• 程序中的第 22 行: for (int j = d - 1; j >= 0; j--) a[j] += p;  对应上图中的黄色部分。p = 100 ( 注意，这时 p 不是 10，因为程序中的第 21 行已经将 p 乘以 10 了 )，d = 8，j = 7 .. 0，表示 0 到 7 这 8 个数字各出现 100 次 ( 00 .. 99)。
• 程序中的第 24 行: a[d] += m;  对应上图中的粉红色部分。d = 8，m = 43，表示 N 的百位数字 8 共出现了 43 次 ( 00 .. 42 )，这是 N 最低两位 ( 42 ) 加一。

至于 0 的计数，需要在最后一轮循环 ( N 的最高位 ) 中扣除无效前导零，如程序中第 23 行: if (n < 10) a[0] -= p + q;  所示，此时 i = 4，n = 5，p = 10000，q = 1111。扣除 p 是为了上图中黄色部分的 0，扣除 q 是为了上图中浅青色部分的 0。

附：上面程序的算法中使用了以下定理：

从 1 到 10 ^r - 1 的正整数，包含 1 .. 9 各 r * 10 ^r-1 个，包含 0 的数目为: r * 10 ^r-1 - ( 10 ⁰ + ... + 10 ^r-1)。

证明如下：

以 r = 3 为例，我们来证明从 1 到 999 的正整数，包含 1 .. 9 各 300 个，包含 0 的数目为: 300 -111 = 189。

首先，考虑 000 .. 999 这 1000 个整数(暂时不丢弃前导零)，每个整数共包含 3 个数字，所以这 1000 个整数包含 3 * 1000 = 3000 个数字。

其次，这 1000 个整数中，0 .. 9 这 10 个数字出现的次数是相同的，也就是说， 0 .. 9 这 10 个数字各出现了 3000 / 10 = 300 次。

最后，让我们来计算前导零的个数，分为以下三种情况：

• 000: 3 * 1 个
• 001 .. 009: 2 * 9 个
• 010 .. 099: 1 * 90 个

总计: 3 * 1 + 2 * 9 + 1 * 90 = 1 + (1 + 9) + (1 + 9 + 90) = 1 + 10 + 100 = 111 个。

所以，扣除前导零后，包含 0 的数目为: 300 -111 = 189。

对于 r 的其他值也可以类似地证明。