Timus 1057. Amount of degrees

Timus 1057. Amount of degrees 要求计算指定范围内能够由 K 个不同的 B 的幂次之和组成的整数的个数。

---

1057. Amount of degrees

Time Limit: 1.0 second
Memory Limit: 16 MB

Create a code to determine the amount of integers, lying in the set [ X; Y] and being a sum of exactly K different integer degrees of B.

Example. Let X=15, Y=20, K=2, B=2. By this example 3 numbers are the sum of exactly two integer degrees of number 2:

17 = 2 ⁴+2 ⁰,
18 = 2 ⁴+2 ¹,
20 = 2 ⁴+2 ².

Input

The first line of input contains integers X and Y, separated with a space (1 ≤  X ≤  Y ≤ 2 ³¹−1). The next two lines contain integers K and B (1 ≤  K ≤ 20; 2 ≤  B ≤ 10).

Output

Output should contain a single integer — the amount of integers, lying between X and Y, being a sum of exactly K different integer degrees of B.

Sample

input	output
15 20 2 2	3

Problem Source: Rybinsk State Avia Academy

---

解答如下：

 1  using  System;
 2 
 3  namespace  Skyiv.Ben.Timus
 4  {
 5     //   http://acm.timus.ru/problem.aspx?space=1 &num=1057
 6     sealed   class  T1057
 7    {
 8       static   void  Main()
 9      {
10         string [] ss  =  Console.ReadLine().Split();
11         uint  x  =   uint .Parse(ss[ 0 ]);
12         uint  y  =   uint .Parse(ss[ 1 ]);
13         int  k  =   int .Parse(Console.ReadLine());
14         int  b  =   int .Parse(Console.ReadLine());
15         int [] maxs  =  {  16 ,  17 ,  17 ,  18 ,  19 ,  21 ,  22 ,  24 ,  27 ,  30  };
16         int  max  =  ( 20   -  k  <  maxs.Length)  ?  maxs[ 20   -  k] :  32 ;
17         uint [,] a  =   new   uint [k  +   1 , max];
18         for  ( int  i  =   0 ; i  <=  k; i ++ ) a[i,  0 ]  =   1 ;
19         for  ( int  j  =   0 ; j  <  max; j ++ ) a[ 0 , j]  =   1 ;
20         for  ( int  j  =   1 ; j  <  max; j ++ )
21           for  ( int  i  =   1 ; i  <=  k; i ++ )
22            a[i, j]  =  a[i, j  -   1 ]  +  a[i  -   1 , j];
23         uint  high  =  BinarySearch(y  +   1 ,  int .MaxValue, k, b, a);
24        Console.WriteLine(high  -  BinarySearch(x, high, k, b, a));
25      }
26 
27       static   uint  BinarySearch( uint  z,  uint  high,  int  k,  int  b,  uint [,] a)
28      {
29         uint  low  =   1 , mid  =   1 , z2  =   0 ;
30         while  (low  <=  high)
31        {
32          mid  =  (low  +  high)  /   2 ;
33          z2  =  GetNth(mid, k, b, a);
34           if  (z2  <  z) low  =  mid  +   1 ;
35           else   if  (z2  >  z) high  =  mid  -   1 ;
36           else   return  mid;
37        }
38         return  mid  +  ((z2  <  z)  ?   1u  :  0 );
39      }
40 
41       static   uint  GetNth( uint  n,  int  k,  int  b,  uint [,] a)
42      {
43         bool [] bs  =  GetNth( new   bool [ 32 ], a.GetLength( 1 )  -   1 , n, k, a);
44         if  (bs  ==   null )  return   uint .MaxValue;
45         int  bit  =  bs.Length  -   1 ;
46         while  ( ! bs[bit]) bit -- ;
47         long  v  =   0 , b2  =   1 ;
48         for  ( int  i  =   0 ; i  <=  bit; i ++ , b2  *=  b)
49        {
50           if  (bs[i]) v  +=  b2;
51           if  (b2  >   int .MaxValue  ||  v  >   int .MaxValue)  return   uint .MaxValue;
52        }
53         return  ( uint )v;
54      }
55 
56       static   bool [] GetNth( bool [] bs,  int  m,  uint  n,  int  k,  uint [,] a)
57      {
58         int  bit  =  Seek(a, k, m, n);
59         if  (bit  +  k  >=  bs.Length)  return   null ;
60        bs[bit  +  k]  =   true ;
61         if  (bit  >=   0 )
62        {
63           if  (n  >  a[k, bit]  +  a[k  -   1 , bit]) GetNth(bs, bit, n  -  a[k, bit], k  -   1 , a);
64           else
65          {
66            GetNth(bs, bit, n  -  a[k  -   1 , bit], k, a);
67            bs[bit  +  k  -   1 ]  =   false ;
68          }
69        }
70         else   for  ( int  i  =   0 ; i  <  k  -   1 ; i ++ ) bs[i]  =   true ;  //  n == 1
71         return  bs;
72      }
73 
74       static   int  Seek( uint [,] a,  int  k,  int  m,  uint  n)
75      {
76         for  ( int  i  =  m; i  >=   0 ; i -- )  if  (a[k, i]  <  n)  return  i;
77         return   - 1 ;
78      }
79    }
80  }

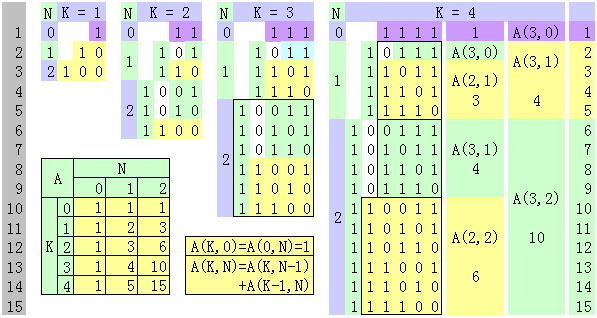
这道题要求计算指定范围内 (从 X 到 Y，1 ≤ X ≤ Y ≤ 2³¹−1) 能够由 K (1 ≤ K ≤ 20) 个不同的 B (2 ≤ B ≤ 10) 的幂次之和组成的整数的个数。

这个程序的关键在于第 41 到 54 行的 GetNth 方法，该方法返回满足以下条件的第 N 个 B 进制整数：该整数中有 K 个 1，其余数字全部都是 0。该方法在第 43 行调用第 56 到 72 行的 GetNth 方法，获得表示该整数的 0 和 1 的布尔数组。然后在第 44 到 53 行根据该布尔数组计算出该 B 进制整数。

而第 56 到 72 行的 GetNth 方法是根据一定的规律计算出所需的布尔数组。该方法在第 58 行调用第 74 到 78 行的 Seek 方法获得最高位的 1 的位置，在第 60 行设置最高位的 1。然后递归调用自身以设置其余的 1，这分为两种情况。第一种情况如图中浅黄色方块所示，对应程序第 63 行，第二种情况如图中浅青色方块所示，对应程序中第 66 到 67 行。如果递归到最后达到 N = 1 的情况，则对应程序中第 70 行。

而程序中第 74 到 78 行的 Seek 方法中使用的二维数组 A 是在主程序中的第 15 到 22 行初始化的。该数组由以下递推公式决定：

A(K, 0) = A(0, N) = 1

A(K, N) = A(K, N-1) + A(K-1, N)

其中 A(K, N-1) 对应前面提到的第二种情况，A(K-1, N) 对应前面提到的第一种情况。

最后，在主程序的第 23 到 24 行调用第 27 到 39 行的 BinarySearch 方法(该方法在第 33 行调用第 41 到 54 行的 GetNth 方法)，使用二分搜索法分别获得最小的 N 使得第 N 个满足条件的 B 进制整数不小于 Y+1 以及不小于 X。最终答案就是这两者之差。

这个程序使用的算法虽然比较复杂，但应该是最优的。这个程序的实际运行时间是 0.078 秒。如果使用蛮力搜索法穷举每种可能，运行时间应该会远远就超出题目限制的 1.0 秒。