Surf算法

前期看了许久的sift算法，总算是有些了解了过程。对于具体算法的一些实现，仍旧是不太明白。对于kd树的建立，和匹配依旧是自己不想写算法，而是利用已经写好的算法做个小实验。vlfeat算法，有实现好的带有匹配的sift算法吗？有知道的童鞋们吗？告知~

正文开始：

surf借鉴了sift中简化近似的思想，将DOH中的高斯二阶微分模板进行了近似简化，使得模板对图像的滤波只需要进行几个简单的加减法运算，并且，这种运算与滤波模板的尺寸有关。实验证明surf算法较sift算法在运算速度上要快3倍左右。

1 积分图像

surf算法中要用到积分图像的概念。借助积分图像，图像与高斯二阶微分模板的滤波转化为对积分图像的加减运算。积分图像（Integral Image）的概念是由viola和Jones提出来的，而将类似积分图像用于盒子滤波是由Simard等人提出。

积分图像中任意一点（i,j）的值为ii(i,j)为原图像左上角到任意点（i,j）相应的对角线区域灰度值的总和即：

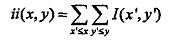
公式中，I(x`,y`)表示原图像中点（i`,j`）的灰度值，ii（x,y）可以由下面两公式迭代计算得到：

公式中，S（x,y）表示一列的积分，且S（i,-1）=0,ii(-1,j)=0.求积分图像，只需对原图像的所有像素素进行一遍扫描。下面的代码为c++语言的实现

pOutImage[0][0] = pInImage[0][0];

for(int x = 1, x < nWidth; i++)
{
  pOutImage[x][0] = pInImage[x-1][0] + pInImage[x][0];

}

for(int y=1; y< nHeight ;y++)
{
  int nSum = 0;

  for(int x=0; x < nWidth;x++)
  {
    nSum = pInImage[x][y];

    pOutImage[x][y]= pInImage[x][y-1]+nSum;
  }

}

如图表示，在求取窗口w内的像元灰度和时，不管窗口W的大小如何，均可利用积分图像的4个对应点（i1,j1）（i2,j2）（i3,j3）（i4,j4）的值计算的到。也就是说，求取窗口W内的像元灰度和与窗口的尺寸是无关的。窗口W内的像元的灰度和为

Sum（W）= ii(i4,j4) -ii(i2,j2) - ii(i3,j3) + ii(i1,j1)

下面看以截图，相信都可以看懂

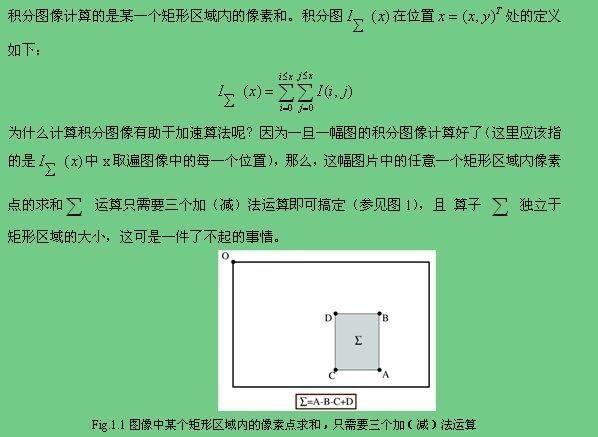
关于矩形区域内像素点的求和应该是一种简单重复性运算，采用这种思路总体上提高了效率。为什么这么说呢？假设一幅图片共有n个像素点，则计算n个位置的积分图总共的加法运算有n-1次（注意：可不是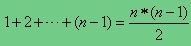次哦，要充分利用递推思想），将这些结果保存在一个跟原图对应的矩阵M中。当需要计算图像中某个矩形区域内的所有像素之和是直接像查表一样，调出A,B,C,D四点的积分图值，简单的加减法（注意只需要三次哦）即可得到结果。反之，如果采用naive的方式直接在原图像中的某个矩形区域内求和，你想想，总共可能的矩形组合有多少？ ！！且对于一幅图像n那是相当大啊，所以2^n

 那可是天文数字，而且这里面绝大部分的矩形有重叠，重叠意味着什么？在算求和的时候有重复性的工作，其实我们是可以有效的利用已经计算过的信息的。这就是积分图法的内在思想：它实际上是先计算n个互不重叠（专业点说是不相交）的矩形区域内的像素点求和，充分利用这些值（已有值）计算未知值，有点类似递推的味道...这就完全避免了重复求和运算。

 这样就可以进行2种运算：

    （1）任意矩形区域内像素积分。由图像的积分图可方便快速地计算图像中任意矩形内所有像素灰度积分。如下图2.3所示，点1的积分图像ii1的值为(其中Sum为求和) :

    ii1=Sum（A）

   

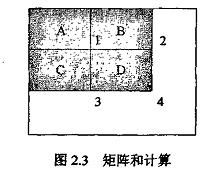
    同理，点2、点3、点4的积分图像分别为：

    ii2=Sum(A)+Sum(B);      ii3=Sum(A)+Sum(C);    ii4=Sum(A)+Sum(B)+Sum(C)+Sum(D);

    矩形区域D内的所有像素灰度积分可由矩形端点的积分图像值得到:

                   Sum(D)=ii1+ii4-(ii2+ii3)            (1)

(2) 特征值计算
    矩形特征的特征值是两个不同的矩形区域像素和之差，由(1)式可以计算任意矩形特征的特征值，下面以图2.1中特征原型A为例说明特征值的计算。

   
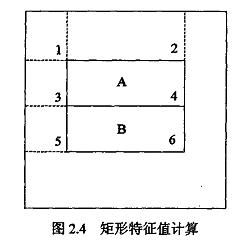
    如图2.4 所示，该特征原型的特征值定义为:

 

    Sum（A）-Sum（B）

 

    根据（1）式则有：Sum(A)=ii4+ii1-(ii2+ii3);    Sum(B)=ii6+ii3-(ii4+ii5);

 

   所以此类特征原型的特征值为:

 

                (ii4-ii3)-(ii2-ii1)+(ii4-ii3)-(ii6-ii5)

 

   另示：运用积分图可以快速计算给定的矩形之所有象素值之和Sum(r)。假设r=(x,y,w,h),那么此矩形内部所有元素之和等价于下面积分图中下面这个式子:

 

                 Sum(r) = ii(x+w,y+h)+ii(x-1,y-1)-ii(x+w,y-1)-ii(x-1,y+h)

 

   由此可见，矩形特征特征值计算只与此特征端点的积分图有关，而与图像坐标值无关。对于同一类型的矩形特征，不管特征的尺度和位置如何，特征值的计算所耗费的时间都是常量，而且都只是简单的加减运算。其它类型的特征值计算方法类似。