文章收录在公众号: bigsai 更多精彩干货敬请关注!
前言
说起八皇后问题,它是一道回溯算法类的经典问题,也可能是我们大部分人在上数据结构或者算法课上遇到过的最难的一道题……
第一次遇到它的时候应该是大一下或者大二这个期间,这个时间对啥都懵懵懂懂,啥都想学却发现好像啥都挺难的,八皇后同样把那个时候的我阻拦在外,我记得很清楚当时大二初我们学业导师给我们开班会时候讲到的一句话很清晰:"如果没有认真的学习算法他怎么可能解出八皇后的代码呢"。
确实,那个时候的我搞不懂递归,回溯也没听过,连Java的集合都没用明白,毫无逻辑可言,八皇后对我来说确实就是无从下手。
浅谈递归
对于递归算法,我觉得掌握递归是入门数据结构与算法的关键,因为后面学习很多操作涉及到递归,例如链表的一些操作、树的遍历和一些操作、图的dfs、快排、归并排序等等。
递归的实质还是借助栈实现一些操作,利用递归能够完成的操作使用栈都能够完成,并且利用栈的话可以很好的控制停止,效率更高(递归是一个来回的过程回来的时候需要特判)。
递归实现和栈实现操作的区别,递归对我们来说更简洁巧妙,并且用多了会发现很多问题的处理上递归的思考方式更偏向人的思考方式,而栈的话就是老老实实用计算机(数据结构特性)的思维去思考问题。这个你可以参考二叉树的遍历方式递归和非递归版本,复杂性一目了然。
从递归算法的特征上来看,递归算法的问题都是父问题可以用过一定关系转化为子问题。即从后往前推导的过程,一般通过一个参数来表示当前的层级。
而递归的主要特点如下:
- 自己调用自己
- 递归通常不在意具体操作,只关心初始条件和上下层的变化关系。
- 递归函数需要有临界停止点,即递归不能无限制的执行下去。通常这个点为必须经过的一个数。
- 递归可以被栈替代。有些递归可以优化。比如遇到重复性的可以借助空间内存记录而减少递归的次数。
而通常递归算法的一个流程大致为:
定义递归算法及参数
- 停止递归算法条件
- (可存在)其他逻辑
- 递归调用(参数需要改变)
- (可存在)其他逻辑如果还是不理解的话就要看我的另一篇文章了:数据结构与算法—递归算法(从阶乘、斐波那契到汉诺塔的递归图解),写的是真的好!
回溯算法
谈完递归,你可能明白有这么一种方法可以使用,但你可能感觉单单的递归和八皇后还是很难扯上关系,是的没错,所以我来讲回溯算法了。
这里插个小插曲。前天(真的前天)有个舍友我们宿舍一起聊天的时候谈到回溯算法,他说回shuo(朔)算法,我们差异的纠正了一下是回su(素)算法,他竟然读错了四年……不知道路过的你们有没有读错的。
咱们言归正传,算法界中,有五大常用算法:贪心算法、分治算法、动态规划算法、回溯算法、分支界限算法。咱们回溯算法就是五大之一,因为回溯算法能够解决很多实际的问题,尽管很多时候复杂度可能不太小,但大部分情况都能得到一个不错的结果。
对于回溯法的定义,百度百科是这么定义的:
回溯算法实际上一个 类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法, 有“通用解题方法”的美称。
对于回溯法,它的核心就是试探和复原。这个自动化的过程就是利用递归去执行,在递归函数执行前去修改尝试,满足条件后向下递归试探,试探完毕后需要将数值复原。在这个试探的过程中找到我们所需要的一个或者所有解。这个我们也俗称暴力。

啥?没听懂?好,那我就再讲讲,你应该知道深度优先搜索(dfs)吧?其实回溯算法就是一种特殊的dfs。之所以叫回溯,就是因为这类算法在运用递归都有个复原的过程,所以前面的操作就相当于试探一样。而这类算法一般常常配对一个或多个boolean类型的数组用来标记试探途中用过的点。
举个例子,我们知道回溯算法用来求所有数字的排列顺序。我们分析其中一个顺序。比如数列6 8 9这个序列的话,我们用来求它的排列顺序。
对于代码块来说,这可能很容易实现:
import java.util.Arrays;
public class test {
public static void main(String[] args) {
int arr[]={6,8,9};//需要排列组合的数组
int val[]={0,0,0};//临时储存的数组
boolean jud[] = new boolean[arr.length];// 判断是否被用
dfs(arr,val, jud, 0,"");//用一个字符串长度更直观看结果
}
private static void dfs(int[] arr, int val[],boolean[] jud, int index,String s) {
System.out.println(s+Arrays.toString(val));
if (index == arr.length){ }//停止递归条件
else{
for (int i = 0; i < arr.length; i++) {
if (!jud[i]) {//当前不能用的
int team=val[index];
val[index] = arr[i];
jud[i] = true;// 下层不能在用
dfs(arr, val, jud, index + 1,s+" _ ");
jud[i] = false;// 还原
val[index]=team;
}
}
}
}
}定义回溯算法及参数
- (符合条件)跳出
- (不符合)不跳出:
- - 遍历需要操作的列表&&该元素可操作&&可以继续试探
- - - 标记该元素已使用以及其他操作
- - - 递归调用(参数改变)
- - - 清除该元素标记以及其他操作也就是在使用数组进行回溯的时候,使用过的时候需要标记子递归不能再使用防止死循环,而当回来的时候需要解封该位置,以便该编号位置被其他兄弟使用之后这个数值在后面能够再次使用!而如果使用List或者StringBuilder等动态空间用来进行回溯的时候记得同样的复原,删了要记得增,减了要记得加。搞明白这些,我想回溯算法也应该难不倒你了吧。
八皇后问题
掌握了回溯算法的关键,八皇后问题多思考就可以想的出来了。前面的讲解都是为了解决八皇后问题做铺垫。首先,我们认真的看下八皇后问题描述。
八皇后问题(英文:Eight queens),是由国际西洋棋棋手马克斯·贝瑟尔于1848年提出的问题,是回溯算法的典型案例。
问题表述为:在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解, 后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转,和对角线对称变换的摆法看成一类,共有42类。计算机发明后,有多种计算机语言可以编程解决此问题。

我们该怎么思考这种问题呢?也就是从何入手呢?
- 从限制条件入手
八皇后问题有以下限制条件:
- 8 x 8的方格
- 每行一个,共八行(0-7)
- 每列一个,共八列(0-7)
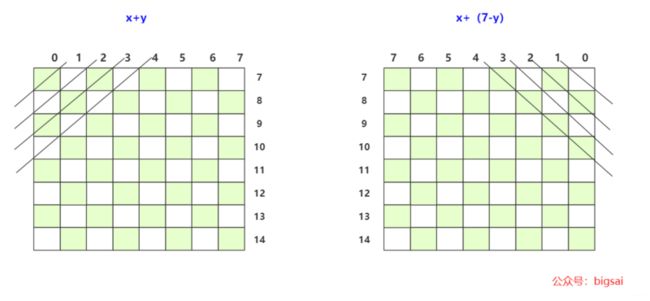
- 每左斜杠一个,共十五左斜杠(0-14)
- 每右斜杠一个,共十五右斜杠(0-14)
当看到这些限制条件,肯定想到这么多限制条件需要判断。判断的话当然就是借助boolean数组啦。还是一维的8个大小,所以我们首先用4个boolean数组用来判断各自的条件是否被满足。
表示这个图的话我们可以使用一个int类型数组表示,0表示没有,1表示有皇后。
那么如何去设计这个算法呢?这个并不是每个格子都有数字,所以在进行回溯的时候不应该每个格子每个格子进行向下递归(同行互斥),也就是递归到当前层的时候,循环遍历该层的八种情况进行试探(每个都试探),如果不满足条件的就不操作而被终止掉,但该行每个满足条件的需要递归的时候需要进入到下一行。
当然你需要提前知道当前位置横纵坐标怎们知道对应的boolean位置(位置从0号开始计算)。例如位置p(x,y)中对应的位置为:
- hang[] :
x每一行就是对应的i。 - lie[] :
y每一列就是对应的j。 - zuoxie[] :
x+y规定顺序为左上到右下 - youxie[] :
x+(7-y)规定顺序为右上到左下(个人习惯)
好啦,该算法的实现代码为:
import java.util.Arrays;
public class EightQueens {
static int allnum=0;
public static void main(String[] args) {
boolean hang[]=new boolean[8];//行
boolean lie[]=new boolean[8];//列
boolean zuoxie[]=new boolean[15];//左斜杠
boolean youxie[]=new boolean[15];//右斜杠
int map[][]=new int[8][8];//地图
dfs(0,hang,lie,zuoxie,youxie,map);//进行下去
}
private static void dfs(int hindex, boolean[] hang, boolean[] lie, boolean[] zuoxie, boolean[] youxie, int[][] map) {
if(hindex==8){
allnum++;
printmap(map);//输出map
}
else{
//hindex为行 i为具体的某一列
for(int i=0;i<8;i++)
{
if(!hang[hindex]&&!lie[i]&&!zuoxie[hindex+i]&&!youxie[hindex+(7-i)])
{
hang[hindex]=true;//试探
lie[i]=true;
zuoxie[hindex+i]=true;
youxie[hindex+(7-i)]=true;
map[hindex][i]=1;
dfs(hindex+1,hang,lie,zuoxie,youxie,map);//dfs
hang[hindex]=false;//还原
lie[i]=false;
zuoxie[hindex+i]=false;
youxie[hindex+(7-i)]=false;
map[hindex][i]=0;
}
}
}
}
//输出地图
private static void printmap(int[][] map) {
System.out.println("第"+allnum+"个排列为");
for(int a[]:map)
{
System.out.println(Arrays.toString(a));
}
}
}跑一边就知道到底有多少种皇后,最终是92种皇后排列方式,不得不说能用数学方法接出来的是真的牛叉。
八皇后变种
此时我想八皇后问题已经搞得明明白白了,但是智慧的人们总是想出各种方法变化题目想难到我们,这种八皇后问题有很多变种,例如n皇后,数独等问题。
这里就简单讲讲两数独问题的变种。
力扣36 有效的数独
像这种题需要考虑和八皇后还是很像,改成9*9,只不过在具体处理需要考虑横、竖和3x3小方格。
当然这题比较简单,还有一题就比较麻烦了 力扣37解数独。
这种二维的回溯需要考虑一些问题,我们对于每一行每一行考虑。 每一行已经预有一些数据事先标记,在从开始试探放值,满足条件后向下递归试探。一直到结束如果都满足那么就可以结束返回数组值。
这里的话有两点需要注意的在这里提一下:
- 用二维两个参数进行递归回溯判断起来谁加谁减比较麻烦,所以我们用一个参数index用它来计算横纵坐标进行转换,这样就减少二维递归的一些麻烦。
- 回溯是一个来回的过程,在回来的过程正常情况需要将数据改回去,但是如果已经知道结果就没必要再该回去可以直接停止放置回溯造成值的修改(这里我用了一个isfinish的boolean类型进行判断)。
结语
好啦,不知道这个专题结束之后能否能够掌握这个八皇后的回溯算法以及思想,能否理清递归,回溯,深搜以及八皇后为关系?
总的来说
- 递归更注重一种方式,自己调用自己。
- 回溯更注重试探和复原,这个过程一般借助递归。
- dfs深度优先搜素,一般用栈或者递归去实现,如果用递归可能会复原也可能不复原数据,所以回溯是深搜的一种。
- 八皇后是经典回溯算法解决的问题,你说深度优先搜素其实也没问题,但回溯更能精准的描述算法特征。
好啦,不说啦,我bigsai去领取佳丽30和白银万两啦!(不错的话记得一键三联,微信搜索bigsai,回复bigsai 下次迎娶美杜莎女王!)