撰前小记:
前些时候穿了几天的薄外套,最终还是败给了广州的天气(太热了)。所以今天还是短袖短裤齐上阵吧,广州的夜,真不冷。
环境准备
本次实验使用TensorFlow 2.3.1。
import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
%matplotlib inline数据描述
使用了Yahoo! Finance ^GSPC的近五年历史股价数据,从2015年11月到2020年11月,共1256个。该数据包含每天股价的信息,如Date, Open, High, Low, Close, Adj Close, Volume。
Tips: 股票小知识
- Date:日期
- Open:开盘价(股票在某一天的起始价)
- High:最高价
- Low:最低价
- Close:收盘价(股票在某一天的最终价)
- Adj Close:加权收盘价
- Volume:总交易额
为简单起见,只使用收盘价作预测。下图直观展示了近五年的收盘价。
代码:
# 用pandas载入数据集
dataframe = read_csv('data/stock_data.csv', usecols=[4], engine='python', skipfooter=3)
data = dataframe.values
# 将整型变为float
data = data.astype('float32')
plt.plot(data)
plt.show()目标
预测未来的股票收盘价,本次预测的是最后56个数据。
构建训练集与测试集
近五年的收盘价是一个长度为 N 的时间序列,定义p0, p1,...,pN-1为每一天的价格。用前 i 个数据预测第 i + 1 个数据构建训练集与测试集,0 < i < N,即
X 0 = (p 0, p 1,..., p i-1)
X 1 = (p i, p i+1,..., p 2i-1)
...
X t = (p ti, p ti+1,..., p (t+1)i-1)
去预测
X t+1 = (p (t+1)i, p (t+1)i+1,..., p (t+2)i-1)
这里选择 i = 6。在LSTM中,time_steps = 6,则训练集可表示为
Input 1 = [p 0, p 1, p 2, p 3, p 4, p 5], Label 1 = [p 6]
Input 2 = [p 1, p 2, p 3, p 4, p 5, p 6], Label 1 = [p 7]
Input 3 = [p 2, p 3, p 4, p 5, p 6, p 7], Label 1 = [p 8]
代码:
# 根据原始数据集构建矩阵
def create_dataset(data, time_steps):
dataX, dataY = [], []
for i in range(len(data) - time_steps):
a = data[i:(i + time_steps), 0]
dataX.append(a)
dataY.append(data[i + time_steps, 0])
return np.array(dataX), np.array(dataY)设定95.55%为训练集,剩下的为测试集:
# 归一化
scaler = MinMaxScaler(feature_range=(0, 1))
data = scaler.fit_transform(data)
# 切割为训练集和测试集
train_size = int(len(data) * 0.9555)
test_size = len(data) - train_size
train, test = data[0:train_size,:], data[train_size:len(data),:]
time_steps = 6
trainX, trainY = create_dataset(train, time_steps)
testX, testY = create_dataset(test, time_steps)
# reshape输入模型数据的格式为:[samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))建立并训练LSTM模型
1层LSTM,隐藏层的神经元个数为128,输出层为1个预测值,迭代次数为100。
Tips: LSTM参数计算
(hidden size × (hidden size + x_dim) + hidden size) × 4
x_dim为输入数据的特征维度,这里是1。
代码:
model = Sequential()
model.add(LSTM(128, input_shape=(time_steps, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['accuracy'])
model.summary()
history = model.fit(trainX, trainY, epochs=100, batch_size=64, verbose=1)
score = model.evaluate(testX, testY, batch_size=64, verbose=1)def visualize_loss(history, title):
loss = history.history["loss"]
epochs = range(len(loss))
plt.figure()
plt.plot(epochs, loss, "b", label="Training loss")
plt.title(title)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
visualize_loss(history, "Training Loss")预测结果
代码:
# 预测训练集与测试集
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# 对预测结果进行反归一化处理
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# 计算训练集与测试集的RMSE
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# 绘制预测结果图
trainPredictPlot = np.empty_like(data)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[time_steps:len(trainPredict) + time_steps, :] = trainPredict
testPredictPlot = np.empty_like(data)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict) + (time_steps * 2)-1:len(data) - 1, :] = testPredict
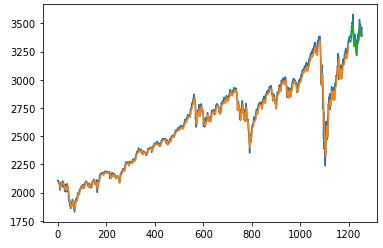
plt.plot(scaler.inverse_transform(data))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()上图中,蓝色线是原始数据,橙色线和绿色线分别是训练集和测试集的预测结果。
参考
https://www.jianshu.com/p/38d...
https://keras.io/examples/tim...