花了好几天的业余时间,看文章,总算是用C实现了一遍红黑树,主要还是自己C语言水平不够高,调试断点浪费了不少时间,闲话少说
1. 红黑树结构体
//这里偷懒就应0代表黑色,1代表红色了
typedef struct RBTreeNode {
int data; //数据域
int color; //0黑色 1红色
struct RBTreeNode *parent;//父亲结点
struct RBTreeNode *left; //左子结点
struct RBTreeNode *right; //右子结点
} RBTreeNode;2. 前序遍历
//这里打印了节点的颜色和父节点
void preOrderTraverse(RBTreeNode *root)
{
if (root != NULL)
{
if (root->parent != NULL)
{
printf("%d color: %d parent:%d\n", root->data, root->color, root->parent->data);
}else{
printf("%d color: %d\n", root->data, root->color);
}
preOrderTraverse(root->left);
preOrderTraverse(root->right);
}
}3.1 左旋
跟AVL树差不多,多了parent相关的操作
/**
* 左旋
* parent parent
* 8 12
* 4 12 8 50
* 9 50 => 4 9 70
* 70
*/
RBTreeNode *left_rotation(RBTreeNode *root)
{
struct RBTreeNode *new_root;
new_root = root->right;
root->right = new_root->left;
//将9的父亲设置为老的root 即8
if (new_root->left != NULL)
{
new_root->left->parent = root;
}
//新root的parent即老parent
new_root->parent = root->parent;
//然后处理老root的parent
if (root->parent == NULL)
{
//老root是根节点
new_root->parent = NULL;
}else{
//判断父亲左右
if (new_root->parent->left == root)
{
new_root->parent->left = new_root;
}else{
new_root->parent->right = new_root;
}
}
root->parent = new_root;
new_root->left = root;
return new_root;
}3.2 右旋
/**
* 右旋
* 8 4
* 4 12 2 8
* 2 6 => 1 6 12
* 1
*/
RBTreeNode *right_rotation(RBTreeNode *root)
{
struct RBTreeNode *new_root;
new_root = root->left;
root->left = new_root->right;
//将6的父亲设置为老的root 即8
if (new_root->right != NULL)
{
new_root->right->parent = root;
}
//新root的parent即老parent
new_root->parent = root->parent;
//然后处理老root的parent
if (root->parent == NULL)
{
//老root是根节点
new_root->parent = NULL;
}else{
//判断父亲左右
if (new_root->parent->left == root)
{
new_root->parent->left = new_root;
}else{
new_root->parent->right = new_root;
}
}
new_root->right = root;
root->parent = new_root;
// printf("***自己right_rotation***: \n");
// printfNode(new_root);
// printf("***左***: \n");
// printfNode(new_root->left);
// printf("***右***: \n");
// printfNode(new_root->right);
return new_root;
}3.3 代码图解
/**
* 1.插入的只有一个根节点
*
* 8(R) => 8(B)
*
* 2.1父节点是黑色,啥也不用干
* 8(B)
* / => 不变
* 4(R)
*
* 2.2 父节点是红色,祖父一定是黑色啦,看叔叔是啥颜色
*
* 2.2.1 父节点是祖父节点的左节点
*
* 2.2.1.1如果叔叔也是红色
* 将父节点,叔节点设为黑色,将祖父节点设为红色,将祖父节点设为“当前节点”(红色节点);即,之后递归继续对“当前节点”进行操作
*
* 8(B) 8(R) 8(B)
* / \ / \ / \
* 4(R) 12(R) => 4(B) 12(B) => 4(B) 12(B)
* / / /
* 2(R) 2(R) 2(R)
*
* 2.2.1.2如果叔叔不存在或是黑色
* 2.2.1.2.1新节点在左子树
* 父节点设为黑色,将祖父节点设为红色,对祖父节点右旋
*
* 8(B) 8(R) 8(B)
* / \ 着色 / \ 对4右旋 / \
* 4(B) 12(B) => 4(R) 12(B) => 2(B) 12(B)
* / / / \
* 2(R) 2(B) 1(R) 4(R)
* / /
* 1(R) 1(R)
*
* 2.2.1.2.2新节点在右子树
* root与父节点交换 并把父节点设为新root的左节点,即转化为2.2.1.2.1,处理如上
*
* 8(B) 8(B) 8(B) 8(B)
* / \ 交换 / \ 着色 / \ 对4右旋 / \
* 4(B) 12(B) => 4(B) 12(B) => 4(R) 12(B) => 3(B) 12(B)
* / / / / \
* 2(R) 3(R) 3(B) 2(R) 4(R)
* \ / /
* 3(R) 2(R) 2(R)
*
*
*
* 2.2.2 父节点是祖父节点的右节点
* 2.2.2.1如果叔叔也是红色
* 将父节点,叔节点设为黑色,将祖父节点设为红色,将祖父节点设为“当前节点”(红色节点);即,之后递归继续对“当前节点”进行操作
*
* 8(B) 8(R) 8(B)
* / \ / \ / \
* 4(R) 12(R) => 4(B) 12(B) => 4(B) 12(B)
* \ \ \
* 20(R) 20(R) 20(R)
*
* 2.2.2.2如果叔叔不存在或是黑色(这里的绘图简化些,其实都一样的)
* 2.2.2.2.1新节点在左子树
* root与父节点交换 并把父节点设为新root的右节点,即转化为2.2.2.2.2
* 8(B) 8(B) 8(R) 10(B)
* \ 交换 \ 着色 \ 对8右旋 / \
* 12(R) => 10(R) => 10(B) => 8(R) 12(R)
* / \ \
* 10(R) 12(R) 12(R)
*
* 2.2.2.2.2新节点在右子树
* 将父节点设为黑色 将祖父节点设为红色 左旋
*
* 8(B) 8(R) 12(B)
* \ 着色 \ 对8左旋 / \
* 12(B) => 12(B) => 8(R) 20(R)
* \ \
* 20(R) 20(R)
*
*
*/4. 自平衡
RBTreeNode *rebalance3(RBTreeNode *root, RBTreeNode *rootNode)//返回新的根节点
{
//1 插入根节点,只需置黑即可
if (root->parent == NULL)
{
root->color = 0;
}
//2 有父节点
if (root->parent != NULL)
{
//2.1 父节点是黑色,啥也不用干
if (root->parent->color == 0)
{
//do nothing
}else{
//2.2 父节点是红色,祖父一定是黑色啦,看叔叔是啥颜色
RBTreeNode *parent, *gparent, *uncle;
parent = root->parent;
gparent = root->parent->parent;
int return_flag = 0;
if (gparent == rootNode)
{
return_flag = 1;
}
//先判断父节点是祖父节点的左节点还是右节点,即叔叔节点是啥
//2.2.1 父节点是祖父节点的左节点
if (parent == gparent->left)
{
uncle = gparent->right;
//2.2.1.1如果叔叔也是红色
if (uncle != NULL && uncle->color == 1)
{
//1.将父节点设为黑色
parent->color = 0;
//2.将叔节点设为黑色
uncle->color = 0;
//3.将祖父节点设为红色
gparent->color = 1;
//4.将祖父节点设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作
return rebalance3(gparent, rootNode);
}else{
//2.2.1.2如果叔叔黑色 或不存在
//2.2.1.2.1 root是左节点
if (root == parent->left)
{
//1.将父节点设为黑色
parent->color = 0;
//2.将祖父节点设为红色
gparent->color = 1;
gparent = right_rotation(gparent);
}else{
//2.2.1.2.2 root是右节点
//1.root与父节点交换 并把父节点设为新root的左节点,即转化为2.2.1.2.1
gparent->left = root;
root->parent = gparent;
root->left = parent;
parent->parent = root;
parent->right = NULL;
return rebalance3(parent, rootNode);
}
}
}else{
//2.2.2 父节点是祖父节点的右节点
uncle = gparent->left;
//2.2.2.1如果叔叔也是红色
if (uncle != NULL && uncle->color == 1)
{
//1.将父节点设为黑色
parent->color = 0;
//2.将叔节点设为黑色
uncle->color = 0;
//3.将祖父节点设为红色
gparent->color = 1;
//4.将祖父节点设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作
return rebalance3(gparent, rootNode);
}else{
//2.2.2.2如果叔叔黑色 或不存在
//2.2.2.2.1 root是左节点
if (root == parent->left)
{
//1.root与父节点交换 并把父节点设为新root的左节点,即转化为2.2.2.2.2
gparent->right = root;
root->parent = gparent;
root->right = parent;
parent->parent = root;
parent->left = NULL;
return rebalance3(parent, rootNode);
}else{
//2.2.2.2.2 root是右节点
//1.将父节点设为黑色
parent->color = 0;
//2.将祖父节点设为红色
gparent->color = 1;
gparent = left_rotation(gparent);
}
}
}
if (return_flag == 1)
{
return gparent;
}
}
}
return rootNode;
}5.1 插入(未平衡)
RBTreeNode *insert(RBTreeNode *root, int data, RBTreeNode *parent)
{
if (NULL == root)
{
return getNode(data, parent);
}
if (data >= root->data)
{
root->right = insert(root->right, data, root);
}else{
root->left = insert(root->left, data, root);
}
return root;
}5.2 插入(平衡)
RBTreeNode *inserRB(RBTreeNode *root, int data, RBTreeNode *parent)
{
root = insert(root,data,parent);
return rebalance3(RBTreeEndNode,root);
}6 测试红黑树构建
int main()
{
struct RBTreeNode *node;
//2.2.1.1 测试用例
node = NULL;
node = inserRB(node, 8, NULL);
node = inserRB(node, 4, NULL);
node = inserRB(node, 12, NULL);
node = inserRB(node, 2, NULL);
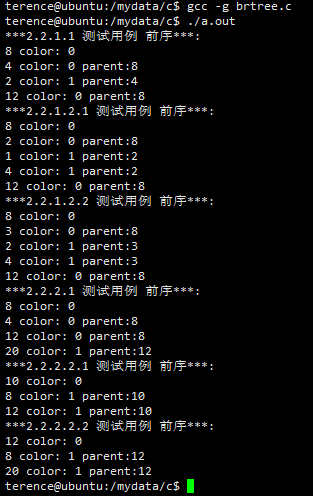
printf("***2.2.1.1 测试用例 前序***: \n");
preOrderTraverse(node);
//2.2.1.2.1 测试用例
node = NULL;
node = inserRB(node, 8, NULL);
node = inserRB(node, 4, NULL);
node = inserRB(node, 12, NULL);
node = inserRB(node, 2, NULL);
node = inserRB(node, 1, NULL);
printf("***2.2.1.2.1 测试用例 前序***: \n");
preOrderTraverse(node);
//2.2.1.2.2 测试用例
node = NULL;
node = inserRB(node, 8, NULL);
node = inserRB(node, 4, NULL);
node = inserRB(node, 12, NULL);
node = inserRB(node, 2, NULL);
node = inserRB(node, 3, NULL);
printf("***2.2.1.2.2 测试用例 前序***: \n");
preOrderTraverse(node);
//2.2.2.1 测试用例
node = NULL;
node = inserRB(node, 8, NULL);
node = inserRB(node, 4, NULL);
node = inserRB(node, 12, NULL);
node = inserRB(node, 20, NULL);
printf("***2.2.2.1 测试用例 前序***: \n");
preOrderTraverse(node);
//2.2.2.2.1 测试用例
node = NULL;
node = inserRB(node, 8, NULL);
node = inserRB(node, 12, NULL);
node = inserRB(node, 10, NULL);
printf("***2.2.2.2.1 测试用例 前序***: \n");
preOrderTraverse(node);
//2.2.2.2.2 测试用例
node = NULL;
node = inserRB(node, 8, NULL);
node = inserRB(node, 12, NULL);
node = inserRB(node, 20, NULL);
printf("***2.2.2.2.2 测试用例 前序***: \n");
preOrderTraverse(node);
}7 红黑树删除节点
@todo