数据结构与算法入门指南
了解各个排序的算法原理比较适合找工作面试的时候用,在刷题竞赛的时候直接使用sort函数即可
sort函数
sort作为C++自带的函数,使用频率比较高,一般遇到需要排序的数组用就行了,能解决大部分需要排序的问题。下面演示一下各种用法。
基础用法
最基础的用法,对数组直接排序(默认从小到大排序)。
int A[10] = { 5,4,8,7,6,4,1,6,5,1 };
sort(A, A + 10); // A = { 1,1,4,4,5,5,6,6,7,8 }sort函数的前两个参数为首地址与尾地址,表示需要排序一段数组。在上例中,A有10个元素,而使用A时会返回A的首地址,A + 10表示在首地址上向后偏移10个位置后的地址,用(A,A + 10)可以表示A[0 ~ 9]。
如果只想对前五位排序,也可以这样写sort(A, A + 5)。
对于STL中的vector也是如此,使用对象中的begin()与end()获取首地址与尾地址。
vector A = { 5,4,6,8,7,4,1,6,9 };
sort(A.begin(), A.end()); // A = { 1,4,4,5,6,6,7,8,9 } 那么对于自定义的结构体呢?看下面。
自定义排序用法
sort函数还有第三个可选参数,就是自定义排序的方法,传入方法名或者匿名函数即可。传入的方法的参数必须是两个同类型的且返回值为bool类型。
如果不使用第三个参数,sort函数会默认调用对象的<方法来比较两个对象的大小关系,使用结构体时需要重写一下operator<。
使用匿名函数
int A[10] = { 5,1,7,9,5,4,8,3,1,0 }; sort(A, A + 10, [](int a, int b) { return a > b; }); //从大到小排序 //A = { 9,8,7,5,5,4,3,1,1,0 }使用方法
//从大到小排序 bool cmp(int a, int b) { return a > b; } int main() { int A[10] = { 5,1,7,9,5,4,8,3,1,0 }; sort(A, A + 10, cmp); //A = { 9,8,7,5,5,4,3,1,1,0 } return 0; }结构体重载
operator<struct Node { int a, b; //按a对Node从小到大排序(与传入的Node比较) bool operator<(Node u) const { return a < u.a; } }; int main() { Node A[3] = { {1, 6}, {8, 0}, {4, 5} }; sort(A, A + 3); // A = { {1, 6}, {4, 5}, {8, 0} }; return 0; }当然,也可以选择不重载
operator<,直接传匿名函数或者方法。
less() 与greater()
如果只是想让元素 从小到大 或者 从大到小 排序,那么大可不必自己手写一个方法实现,直接使用系统内置的less与greater即可,T为元素类型。
sort(A, A + 10, less()); //从小到大排序
sort(A, A + 10, greater()); //从大到小排序 less需要类重载() operator<()greater需要类重载() operator>()
快速排序与归并排序都用了递归实现,如果你对递归并不是很熟练,可以大概了解后暂时跳过,以后再回来看看。
QuickSort 快速排序
快速排序先会随机找一个基准点,把小于基准点的数放到左边,把大于基准点的数放到右边,再将区间划分为两半递归执行,一直如此划分下去,就达到了排序的目的。
具体的排序方法:确定基准点后,双指针从数组两端向中间移动,左边指针先找到大于基准点的,然后右指针移动到小于基准点的,交换两个指针的数值即可。
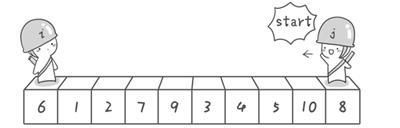
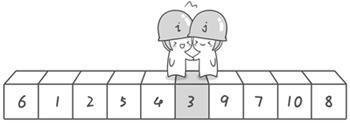
引用一下《啊哈!算法》这本书中的快速排序流程图,将双指针看成两个哨兵。(以左端点6为基准点,右指针先出发)
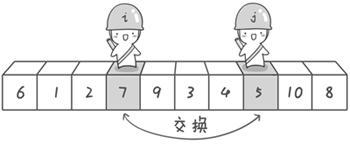
左右指针找到符合条件的值,交换!
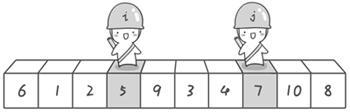
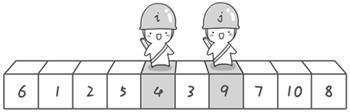
交换完之后继续查找,找到后继续交换,直到两个哨兵(双指针)相遇为止。
两个哨兵相遇后,我们要把基准值放到相遇的位置,也就是中间,毕竟左边都是比基准值小的,右边都是比基准值大的数嘛。
到此第一轮排序完毕,但我们发现整个数组其实并没有完全排好序,接下来需要将其不断分成左右两个区间重复上述过程最后就能将整个数组排序完毕了。
下面我们来写写代码吧,上模板题!(代码实现与上述过程有所差异,不过原理大致相同)
P1177 【模板】快速排序 (注意:该题如果随机选取的数为最左边的数,即x = A[L],则会超时)
#include
using namespace std;
const int maxn = 100000 + 10;
int n, A[maxn];
void quick_sort(int l, int r)
{
if (l >= r) return; //不能再划分区间了,终止
//x为随机选取的值,i为起点,j为终点。
int x = A[(l + r) / 2], i = l - 1, j = r + 1;
while (i < j)
{
while (A[++i] < x); //找出左边大于x的值 (当A[j] > x 时循环停止 即目前A[j] > x
while (A[--j] > x); //同理找出右边小于x的值
if (i < j) swap(A[i], A[j]); //如果符合要求则交换
}
quick_sort(l, j); //继续划分左边
quick_sort(j + 1, r); //划分右边
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
cin >> A[i];
quick_sort(0, n - 1);
for (int i = 0; i < n; i++)
cout << A[i] << ' ';
return 0;
} MergeSort 归并排序
归并排序与快速排序最大的不同就是 快速排序是先排序再划分,而归并排序是先划分再排序,其中间过程可以理解为合并两个有序数组(这一步需要开额外空间实现)。
合并两个有序数组的方法:比较两个数组开头的数,谁小就选谁,最后如果有数组不为空,则一次性全部选取即可。具体题目:88. 合并两个有序数组
我们没有对数组排过序,又怎么会得到有序数组让我们合并呢,其实划分最终会划分到每个元素上,对于单个元素而言不需要在意顺序了。
依旧可以使用上面的题目来练手归并排序 P1177 【模板】快速排序
#include
using namespace std;
const int maxn = 100000 + 10;
int n, A[maxn], B[maxn];
void merge_sort(int l, int r)
{
if (l >= r) return;
int mid = (l + r) / 2; //找出中点
merge_sort(l, mid); merge_sort(mid + 1, r); //划分两边
//合并两个有序数组(当划分到只有一个元素的时候也是有序的)
int k = l, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (A[i] <= A[j]) B[k++] = A[i++];
else B[k++] = A[j++];
//两个数组合并完毕,只要数组中有元素就放进去(只要一组有,可以保证另一组为空,所以不用做判断)
while (i <= mid) B[k++] = A[i++];
while (j <= r) B[k++] = A[j++];
for (i = l; i <= r; i++) A[i] = B[i]; //将排序好的数组覆盖放入原数组中
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
cin >> A[i];
merge_sort(0, n - 1);
for (int i = 0; i < n; i++)
cout << A[i] << ' ';
return 0;
} 关于其他排序算法
大部分算法的时间复杂度与空间复杂度都没有快速排序与归并排序好,所以这里就不一一细说了,列举一下其他常见的排序算法,有兴趣可以自己了解了解。
- 冒泡排序
- 插入排序
- 希尔排序
- 选择排序
- 桶排序
- 计数排序
- 基数排序
- ...
题目
题目列表待增加,洛谷的官方题单是个不错的选择。