poj 2125 有向图破坏，求拆掉图中所有边的最小代价

对于每个点有两个数in[i],out[i]，表示拆掉i的所有入边的代价和拆掉所有出边的代价

对于一条边(u,v)有两种操作可以将其拆掉，要么拆除u的所有出边，要么拆除v的所有入边，两个操作至少要有一个被执行

这就相当于最小点权覆盖（可以参考那篇最小割的论文）中的一条边中的任意一个点都可以覆盖这条边

所以，一个操作看做一个点，一条边相当于连接两个操作的边，一个最小点权覆盖的模型就建立好了

建图过程如下：

新建源点汇点s、t

对于每个点u，拆成u u+n

s->u 容量为out【u】；

u+n->t容量为in[u]

对于每条边u->v

u->v+n,容量为无穷大

求最小割，可得最小代价，（画个简单的图模拟一下就知道为什么这样子是对的啦）

然后是输出方案

直接从s开始搜，(1-n)中不能搜到的点为选择拆除出边操作的点

（n+1-->2*n）中能搜到的点为选择拆除入边操作的点，因为已经求过最小割了，所以这些点（s能搜到的）与t可定已经分开了

注意:最小割对应的是简单割(因为中间的边都有无穷大的容量)，哪条边被割了，就相当于选择了对应的某个操作

比如

与源点连接的边是割边，表示拆除a的出边这个操作

与汇点。。。。。。

附一张简单的图

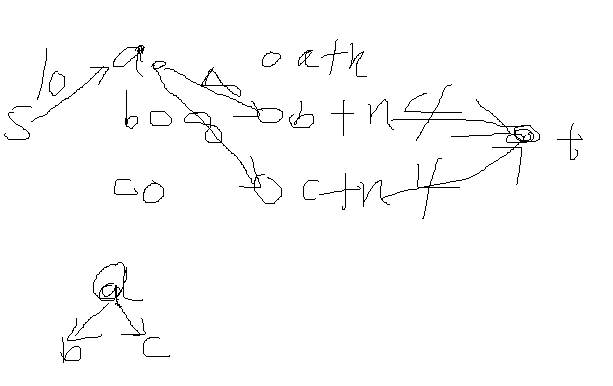
图中拆除a的出边要花费10，拆除b、c的入边都花费4，最小割为8，

所以肯定是选择了b+n->t与c+n->t这两条割边，即选择了拆除b的入边，与拆除c的入边这两个操作

如果两个4变为两个6，则最小割容量为10，选择s->a这条割边，即选择拆除a的出边这个操作

这样子讲，应该比较清楚了吧

View Code

#include<stdio.h>
#include<string.h>
const int MAX=1010;
const int INF=1000000000;
struct
{
    int v,c,next;
}edge[1000000];
int E,head[MAX];
int gap[MAX],cur[MAX];
int pre[MAX],dis[MAX];
void add_edge(int s,int t,int c,int cc)
{
    edge[E].v=t; edge[E].c=c;
    edge[E].next=head[s];
    head[s]=E++;
    edge[E].v=s; edge[E].c=cc;
    edge[E].next=head[t];
    head[t]=E++;
}
int min(int a,int b){return (a==-1||b<a)?b:a;}
int SAP(int s,int t,int n)
{
    memset(gap,0,sizeof(gap));
    memset(dis,0,sizeof(dis));
    int i;
    for(i=0;i<n;i++)cur[i]=head[i];
    int u=pre[s]=s,maxflow=0,aug=-1,v;
    gap[0]=n;    
    while(dis[s]<n)
    {
loop:    for(i=cur[u];i!=-1;i=edge[i].next)
        {
            v=edge[i].v;
            if(edge[i].c>0&&dis[u]==dis[v]+1)
            {
                aug=min(aug,edge[i].c);
                pre[v]=u;
                cur[u]=i;
                u=v;
                if(u==t)
                {
                    for(u=pre[u];v!=s;v=u,u=pre[u])
                    {
                        edge[cur[u]].c-=aug;
                        edge[cur[u]^1].c+=aug;
                    }
                    maxflow+=aug;
                    aug=-1;
                }
                goto loop;
            }
        }
        int mindis=n;
        for(i=head[u];i!=-1;i=edge[i].next)
        {
            v=edge[i].v;
            if(edge[i].c>0&&dis[v]<mindis)
            {
                cur[u]=i;
                mindis=dis[v];
            }
        }
        if((--gap[dis[u]])==0)break;
        gap[dis[u]=mindis+1]++;
        u=pre[u];
    }
    return maxflow;
}
int in[MAX],out[MAX];
int n,m;
int flag[MAX];
void dfs(int u)
{
    flag[u]=1;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].v;
        if(edge[i].c&&!flag[v])
            dfs(v);
    }
}
int main()
{
    int i,j,a,b;
    scanf("%d%d",&n,&m);
    memset(head,-1,sizeof(head));E=0;
    int s=0,t=2*n+1;
    for(i=1;i<=n;i++) scanf("%d",&in[i]),add_edge(i+n,t,in[i],0);
    for(i=1;i<=n;i++) scanf("%d",&out[i]),add_edge(s,i,out[i],0);
    for(i=1;i<=m;i++)
    {
        scanf("%d%d",&a,&b);
        add_edge(a,b+n,INF,0);
    }
    int min_cut=SAP(s,t,2*n+2);
    memset(flag,0,sizeof(flag));
    dfs(s);
    int ans=0;
    for(i=1;i<=n;i++)
    {
        if(flag[i]==0) ans++;
        if(flag[i+n]==1) ans++;
    }
    printf("%d\n",min_cut);
    printf("%d\n",ans);
    for(i=1;i<=n;i++)
    {
        if(flag[i]==0) printf("%d -\n",i);
        if(flag[i+n]==1) printf("%d +\n",i);
    }
    return 0;
}