简介: 你有多久没读过学术论文了?高水平论文多为英文,笔者翻译了一篇 2013 年 Google 的 DeepMind 的深度强化学习论文,这篇文章被视为 强化学习+深度学习 的里程碑之作,其成果于 2015 年发表在了顶级学术期刊Nature上。这篇文章的内容是, CNN(卷积神经网络) + Q-learning(一种离轨-时序差分-强化学习迭代方法)= DQN ,让神经网络自己学习玩雅达利小游戏(上个世纪70/80年代的电子游戏,控制规则很简单直接)。整个思路特别简单,对于2020年的强化学习初学者来讲,这真的只是一个入门级的小作业(也许只需要几行代码),因为现在已经有了很多成熟的深度学习框架+强化学习框架+测试环境封装。
今天,我们抛开代码,尝试感受论文的魅力;并且设身处地地想一想:如果你现在是处于 2013 年的科技爱好者,看到这个成果,该有多震惊、多喜悦?
文章:Mnih V , Kavukcuoglu K , Silver D , et al. Playing Atari with Deep Reinforcement Learning[J]. Computer Science, 2013. DeepMind链接:(https://deepmind.com/research/publications/playing-atari-deep-reinforcement-learning)
使用深度强化学习操控雅达利游戏
前置知识
很多程序猿朋友可能不太了解强化学习算法,实际上,这就是一种自动控制技术。我们可以将强化学习视为一个黑箱: 我们向黑箱中输入环境的信息(如你在游戏中的位置以及敌人的位置、周边的地理条件等),黑箱立即输出此可你应该做什么(如射击、向左移动1米、向右移动1米等) 。强化学习就是基于这个框架进行拓展,这其中有很多内容值得研究:如何通过少量的数据对黑箱中的函数进行高效训练(强化学习的数据都是基于与环境交互得来,数量很少)?多个黑箱间如何通讯协作?
我将强化学习的参数迭代简单抽象为下面的框架。
for ep in range(epoch):
# 环境初始化后
# 我们得到当前环境的信息:obs
# 以及现在这个环境是否结束
# (比如这句游戏是否结束):done
obs, done = env.reset()
# 强化学习与环境交互 n_step 次后
# 用获得的数据更新一次参数
# 因此要有 step_ 计数
step_ = 0
while not done:
if step_ == n_step:
# buffer 中存储着历史数据
# 只与如何 learn() 是数学问题
# 有很多研究成果,如 TRPO PPO
agent.learn(buffer)
step_ = 0
step_ += 1
# agent 根据当前环境,做出动作 action
action = agent.act(obs)
# 环境根据 agent 如何动作,进入下一帧
obs, reward, done, _ = env.step(action)
# 将获得的数据存入 buffer
buffer.add(obs, reward, done)
"""
这里再解释一下 reward
reward 是根据当前情况给强化学习的奖励值
比如,强化学习操作很烂,玩射击游戏死了
reward 就是负数
强化学习就会通过算法迭代知道:
“之前我的操作很烂,这么做 action 不行”
相反,强化学习操作很好,射死了好多玩家
最终的 reward 可能就是正数
强化学习就会通过算法迭代知道
“这局我的操作很好,这么做 action 值得巩固”
"""这篇文章中,我们将看到几乎第一个“有用的”、“超越人类”的通用强化学习算法DQN。文章是我人工翻译的,欢迎指正! 下面我们开始!
摘要
我们提出了首个能够直接从高维场景成功中学习到控制策略的深度强化学习模型。(Piper蛋窝批注:注意直接二字,直接将图形输入神经网络,就好像人类用眼睛直接看到图像一样,完全模仿人操作游戏的情景)模型由卷积神经网络组成,基于Q-learning的变体进行训练, 输入是未经处理的像素,而输出是评价未来奖励的值函数。 (Piper蛋窝批注:即输出是各个动作的价值,如果想进行最优控制,则选择价值最高的动作进行执行即可)我们在Arcade学习平台中,将我们的方法应用到了7个雅达利2600游戏上,且不需要对算法结构做任何调整。(Piper蛋窝批注:现在已经不需要这么麻烦,直接再 python 中 pip 雅达利即可)我们发现有6个游戏的表现超过了已有方法,并且它们中有三个超过了人类高手的控制水平。
1 介绍
从类似视觉或语言的高纬度场景输出中,直接学习智能体控制方法是强化学习中存在已久的难题之一。这个领域大部分成功的强化学习应用都依赖人工构造的特征值与线性价值函数或策略设计。简言之,这类系统的表现高度依赖特征设计的质量。 (Piper蛋窝批注:人工提取特征,就是根据不同问题进行不同设计,这不“智能”)
深度学习的近期发展让从场景信息中直接提取高阶特征成为可能,代表性的突破有计算机视觉以及语音识别。 这些方法利用了大量的神经网络模型,包括卷积神经网络、多层感知机、受限玻尔兹曼机和循环神经网络,在监督学习与非监督学习领域都发挥了作用。顺着这个思路,我们很自然地考虑是否能基于类似的技术,将强化学习与场景数据结合。
然而,强化学习与深度学习结合面临几个挑战。首先,当下大部分成功的深度学习应用需要大量的手动标记的训练数据。另一方面,强化学习算法必须以一个标量的奖励信息为学习对象。然而,该奖励信息往往是稀疏的、有噪声的、有延迟的。在动作与其造成的结果之间的延迟,往往长达几千步长的时间。在延迟的情况下,对于监督学习,在输入与目标间建立联系是十分艰难的。另一个问题是,大部分深度强化学习假设了数据样本是独立的, 而在强化学习中,需要处理的序列往往是高度相关的状态。此外,在强化学习中,数据分布随着算法学习到新的行为会发生改变,这与基于稳定分布的深度学习方法产生了冲突。
本文证实了卷积神经网络能够克服这些问题,从复杂的强化学习环境的视频数据中成功学习到控制策略。 这个网络结构通过Q-learning的变体进行训练,与此同时使用梯度下降策略来更新权重。 为了缓解相关数据与不稳定的分布问题,我们使用了一个经验池机制,经验池可以随机采样以前的状态转换,进而在大量旧行为的基础上达到平滑训练分布的效果。 (Piper蛋窝批注:现在几乎所有的深度强化学习方法,都会使用经验池,否则,对于数据是一种浪费 / 利用不充分)
我们在The Arcade学习环境中对大量雅达利2600游戏测试了我们的方法。雅达利2600对于强化学习测试来讲富有挑战性, 它为智能体提供了高维的图形输入($210\times160$ RGB 60Hz的视频)以及为人类玩家设置的有难度的丰富多样的有趣任务。我们的目的是创建一个单一的神经网络智能体能够成功学会控制尽可能多的游戏。 我们没有为网络提供任何其他有关游戏的特殊信息或人工构建的特征值,网络也不会知道模拟器内部的状态。用于网络学习的 只有视频输入、奖励值、终止信号与可能的动作集合——即人类玩家能获取的信息。 此外,网络结构与训练得出的所有超参数在游戏间都是不改变的。目前该网络模型的表现在测试的七个游戏中的六个超过了所有以往的强化学习算法,并且在三个游戏中超过了人类高手的水平。图1展示了五个用于训练的游戏截屏。
2 背景
我们将任务考虑为智能体与环境$\xi$、雅达利模拟器、序列化的动作、观测值与奖励值进行交互。在每一步中,智能体从动作集合$A=\{1,\ldots,K\}$中选择一个动作$a_t$。动作被传递给模拟器,模拟器内在的状态与游戏分数发生改变。通常环境$\xi$是可能是随机的。模拟器的内部状态并不被智能体所观测;取而代之的是一张来自模拟器的图片$x_t\in R^d$,这张图片是由代表当前屏幕信息的像素向量组成。 值得注意的是,通常来讲,游戏的分数取决于整个之前发生的动作与观测值序列;关于某一个动作的反馈只会在几千步发展后显现。
既然智能体只能观测到当前屏幕的图片,这个任务就只能被部分得观测而许多模拟器的状态在感知上是有偏的。比如,只从当前屏幕状态$x_t$完全理解当前的情况是不可能的。 因此,我们考虑将动作与观测值序列化,$s_t=x_1,a_1,x_2,\ldots,a_{t-1},x_t$,并且从这些序列中学习游戏策略。 模拟器中的所有策略都被假设为在有限的步骤内终止。这个形式构建了一个极大的并且有限的马尔科夫决策过程,其中每个序列都是一个确定的状态。 由此,我们可以将标准的强化学习方法应用于这个马尔科夫决策过程,只需简单地将完整的序列$s_t$作为$t$时刻的状态。
智能体与环境交互并进行决策的目的是最大化远期奖励值。我们做出了基本的假设:未来的奖励由参数$\gamma$递减,并且定义了t时刻的折扣回报$R_t=\sum_{t^\prime=t}^{T}\gamma^{t^\prime-t}r_{t^\prime}$,其中T是终止时间。我们定义了最优动作价值函数$Q^\ast\left(s,a\right)$,作为任何策略下的最大期望可行动作回报。具体来讲,就是在观测到状态序列$s$后,选择某个动作$a$,依据$Q^\ast\left(s,a\right)=\max_\pi{E\left[R_t\middle|\ s_t=s,a_t=a,\pi\right]}$,其中$\pi$是序列至动作(或动作的分布)的映射。
最优的动作价值函数遵守重要的贝尔曼等式的准则。具体来讲就是:如果当前序列$s^\prime$的最优价值$Q^\ast\left(s^\prime,a^\prime\right)$的下一步所有可能的动作$a^\prime$可知,那么最优策略就是选择最优动作$a^\prime$来使期望价值最大,即$r+\gamma Q^\ast\left(s^\prime,a^\prime\right)$,
$$Q^\ast\left(s,a\right)=E_{s^\prime~\xi}\left[r+\gamma\max_a^\prime{Q^\ast\left(s^\prime,a^\prime\right)}\middle|\ s,a\right]$$
这是许多强化学习算法的基础思想,目的是估计动作价值函数,手段是通过使用贝尔曼方程作为迭代更新的依据, (Piper蛋窝批注:想说明的是,强化学习的迭代式之所以如此建立,是因为其有坚实的数学基础证明其有效) $Q_{i+1}\left(s,a\right)=E\left[r+\gamma\max_{a^\prime}{Q_i\left(s^\prime,a^\prime\right)}\middle|\left(s,a\right)\right]$。这个价值迭代算法集中在最优动作价值函数上,$Q_i\rightarrow Q^\ast$中$i\rightarrow\infty$。在实践中,这个基础的方法是非常不现实的,因为动作价值函数由每个序列分开估计,没有泛化。取而代之的常见方法是,使用一个函数逼近器去估计动作价值函数的值,$Q\left(s,a;\theta\right)\approx Q^\ast\left(s,a\right)$。 在强化学习社区中,使用线性函数逼近器是很常用的方法,但是有时也会使用非线性函数逼近器替代,比如一个神经网络。 我们使用了一个神经网络函数逼近器作为Q-network,其中的权重为$\theta$。Q-network可以通过最小化损失函数$L_i\left(\theta_i\right)$序列来训练,对于每代$i$,
$$L_i\left(\theta_i\right)=E_{s,a~\rho\ \left(\cdot\right)}\left[\left(y_i-Q\left(s,a;\theta_i\right)\right)^2\right]$$
其中,$y_i=E_{s^\prime~\xi}\left[r+\gamma\max_{a^\prime}{Q\left(s^\prime,a^\prime;\theta_{i-1}\right)}\middle|\ s,a\right]$是第$i$次迭代的目标,$\rho\left(s,a\right)$是我们根据行为分布进行描述的序列$s$和动作$a$概率分布。在优化损失函数$L_i\left(\theta_i\right)$时,上一代参数$\theta_{i-1}$保持不变。 注意,目标函数取决于网络权重;这点区别于监督学习的目标值,在监督学习中,目标值在开始学习前就是固定的。 基于权重对损失函数进行推导,我们得到如下梯度,
$$\nabla_{\theta_i}L_i\left(\theta_i\right)=E_{s,a~\rho\left(\cdot\right);s~\xi}\left[\left(r+\gamma\max_{a^\prime}{Q\left(s^\prime,a^\prime;\theta_{i-1}\right)}-Q\left(s,a;\theta_i\right)\right)\nabla_{\theta_i}Q\left(s,a;\theta_i\right)\right]$$
比起基于上述梯度公式计算整个期望值,我们常常采用通过随机梯度下降的方法优化损失函数。如果权重在每一步都被优化,并且期望值被行为分布$\rho$与模拟器$\xi$单一的样本更新,我们就相当于使用了熟悉的Q-learning算法。(Piper蛋窝批注:这个公式并非很难理解,如果你熟悉 Q-Learning ,这几年,研究人员提出了更加高效的迭代式,可见 TRPO PPO2 等)
值得注意的是,这个算法是无模型的:在算法中只需直接使用模拟器$\xi$中的样本来解决强化学习任务,无需额外为$\xi$构建一个估值函数。 同时,这个算法也是离轨的:算法从贪婪策略$a=\max_a{Q\left(s,a;\theta\right)}$中学习,这个贪婪策略遵循一个能保证对状态空间进行合适探索的行为分布。 在实践中,行为分布遵循$\epsilon-greedy$策略的选择,在这个策略中,有$1-\epsilon$的概率选择行为分布,而有$\epsilon$概率随机选择策略。(Piper蛋窝批注:这也是强化学习的基本思想之一,用白话解释就是,我们不能刚开始尝试,尝到了甜头,就按照那个方向一味进行下去;开始时,我们要鲁莽一点,到处试试,找最好的方向,并学习下去;到了后期,我们保守一点,不再贪婪)
3 相关工作
也许最为知名的成功强化学习案例是TD-gammon,一个操作西洋双陆棋的程序,完全由强化学习与自我博弈进行学习。这个案例中,强化学习获得了超人类的水平。TD-gammon使用了一个类似于Q-learning的无模型强化学习算法,以及一个有一个隐藏层的多层感知机近似价值函数(事实上,TD-Gammon使用了近似的状态价值函数$V\left(s\right)$,而不是动作价值函数$Q(s,a)$,并且其在自我博弈的过程中,学习是同轨的)。(Piper蛋窝批注:这里是论文的文献综述部分,可以看出,这篇文章中的很多思想并非独创的,其站在了巨人们的肩膀上)
然而,早期对于TD-gammon的尝试,包括上述同样的方法来下棋,Go方法与checkers方法就并未如此成功。这造成了一个广为流传的观点:TD-gammon方法是一个特例,只能在西洋双陆棋上生效。也许是因为骰子的随机性帮助了状态空间的探索并且让价值函数变得尤其平滑。
此外, 将无模型的强化学习算法比如Q-learning与非线性逼近器结合,或者使用离轨学习被证明会造成Q-network的有偏。 因此,强化学习的主要研究都被放在了基于线性函数的逼近,以保证更好的收敛。
近期, 将深度学习与强化学习结合成为一股热潮。深度神经网络被用于预测环境$\xi$的变化;受限玻尔兹曼机被用于预测价值函数或者策略。此外,Q-learning的偏差问题通过梯度时序差分的方法部分地解决了。 这些方法被证明在使用一个非线性函数逼近器估值一个固定策略时,或基于Q-learning的迭代框架使用一个线性函数逼近器进行控制时是收敛的;然而,这些方法没有被推广到非线性控制。
也许之前与我们的工作最为相似的就是神经适应性Q-learning(NFQ, neural fitted Q-learning)。NFQ最优化了2式中的损失函数序列,使用了RPROP算法去更新Q-network中的参数。然而,NFQ使用了一个批量数据去更新,每次迭代所花费的算力与数据集的大小是成比例的。相比之下,我们设计的随机梯度更新有着很低的常数更新算力花费,并且适用于大型数据集。NFQ在实际生活中的控制任务中也很成功,其使用了纯图像输入,通过深度自编码技术来学习到一个低纬度的任务描述,然后将其应用到NFQ中。 相比之下,我们将强化学习应用到了端到端,直接从图像中获取输入信息;最终强化学习可以直接从中获取与显著的动作价值有关的特征值。 Q-learning在NFQ中也应用了经验回放以及一个简单的神经网络,但是只接收一个低纬度的状态输入,而非原图像信息。
将雅达利2600模拟器作为强化学习学习平台受[Marc G Bellemare, Yavar Naddaf, Joel Veness, and Michael Bowling. The arcade learning environment: An evaluation platform for general agents. Journal of Artificial Intelligence Research, 47:253–279, 2013.]的启发,该研究使用了基于线性函数逼近器与通用的图像特征的标准强化学习算法。随后,基于使用大量的特征值,并将哈希快排随机地应用到特征值中来降低空间维度,结果有所提升。HyperNEAT的迭代结构被应用到了雅达利平台,在这里还使用了神经网络输出策略的使用训练(对每个游戏分布训练)。使用固定的游戏配置产生的序列进行重复训练后,这些策略能够在某几个雅达利游戏中利用到设计的缺陷。
4 深度强化学习
近期在计算机视觉与语言识别上的图片都依赖于基于大型数据集上对深度神经网络有效的训练。最成功的工作就是直接使用未处理输入数据训练,使用基于随机梯度下降的轻量的更新方法。通过为深度神经网络输入足够的数据,通常能够得到比人手工制作特征更好的学习效果。 这些成果启发了我们对于强化学习的应用。我们的目标是将一个强化学习算法与一个深度神经网络相结合,这其中,直接输入RGB图像,并且通过随机梯度下降高效进行训练过程。
Tesauro的TD-Gammon模型为我们的最开始的工作提供了许多启发。 这个模型对估计价值函数的网络的参数进行更新,直接使用同轨策略经验下的样本,$s_t,a_t,r_t,s_{t+1},a_{t+1}$,这些样本来自算法与环境的交互(或者在西洋双陆棋中的自我博弈)。考虑到这个方法能在20年轻就有着超过最佳人类西洋双陆棋选手的表现,以及这20年硬件的发展,使用现代化的深度神经网络结构以及可扩展的RL算法也许会得到很明显的效果。
与TD-Gammon和类似的在线算法不同,我们使用了一个被称为“经验回放”的技术。 我们将智能体在每步的经验$e_t=\left(s_t,a_t,r_t,s_{t+1}\right)$存储在数据集$D=e_1,\ldots,e_N$中,将许多幕的经验都放在经验池中。 在算法的内部循环中,我们从经验池$e~D$中随机采样,应用Q-learning的更新式或使用小批量的更新。在经验回放完毕后,智能体根据$\epsilon$贪婪策略选择并执行动作。 考虑到使用某个规定的历史信息输入到神经网络中是困难的,我们的Q函数工作在一个由$\Phi$函数产生的固定的历史信息上。挣个算法被称为深度Q-learning,如算法1所示。
这个方法比标准的在线Q-learning多出几个优势。首先,经验池中的每一步都有机会被多次用于权重更新,这让数据有了更高的效率。第二,直接从连续的样本中学习是低效的,因为样本间关联性较强;随机采样打破了这个关联性因此降低了更新的方差。第三,在线学习中当前参数决定了之后用于训练参数的数据样本。比如,如表最优动作是向左移动,那么训练样本将会是在左侧部分的采样;如果最优动作向右,那么训练的分布也会改变。很容易推测出,在这种情况下得到的反馈循环会很不尽人意,并且卡死在一个较差的局部解中,甚至可能灾难性地不收敛。通过使用经验回放技术,行为的分布通常是超过许多过去产生的状态的,这使得我们的学习更加平滑,并且避免了参数的摇摆或不收敛。 值得注意的是,通过经验回放来学习时,使用离轨策略是很必要的(因为我们当前的参数与用于产生数据的不同),因此,我们选择了Q-learning。(Piper蛋窝批注:所谓离轨 off-policy 就是,我们并不马上使用我们刚刚动作产生的数据进行训练,而是我们已经进步了/改善了一些习惯,再拿其他习惯下的数据进行训练)
在实践中,我们的算法只在经验池中存储最近N步的经验元组, 并且均匀地从$D$中随机采样用于更新。这个方法在某些方面进行了限制,因为经验池不会分辨出重要的元组,并且会因为经验池有限的空间$N$用最近的元组覆盖旧的。 同样地,均匀采样让经验池中的所有元组具有同等重要性。一个更加随机化的策略可能是从我们能学到最多的样本中采样,与优先采样类似。
4.1 预处理和模型结构
直接从$210\times160$像素大小、有$128$个颜色的雅达利帧图像中进行工作,这需要大量的计算力,因此我们进行了一个基本的预处理,用于降低输入维度。 未加工的帧图像首先通过其RGB值1转换为灰度图像,并且下采样为$110\times84$的图形、最终输入为$84\times84$大小图像,其大概包括了玩家区域。我们只需要最终的图像,因为我们使用了[Alex Krizhevsky, Ilya Sutskever, and Geoff Hinton. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25, pages 1106–1114, 2012.]中的2D卷积,这个卷积需要方形输入。在本文的算法那中,算法1中的函数$\Phi$就是对最近的四帧动画进行了预处理,并且将其堆叠作为$Q$函数的输入。
使用神经网络将Q参数化有几个方式。考虑到Q是历史动作数据对于动作价值的映射,历史数据与动作数据可以被用于作为神经网络的输入,这些手段已经有人使用。 这种结构的主要缺点就是,在前进时需要对每个动作的价值进行计算,造成了与动作数量成正比的巨大计算成本。关于单个动作的估计价值的输出只与输入状态有关。这种做法的主要好处是,在给定状态时,能够通过神经网络计算所有动作的价值。
现在来讨论适用于全部其中雅达利游戏的结构。神经网络的输入由一个$\Phi$函数产生的$84\times84\times4$的图片构成。第一个隐层由$168\times8$尺寸的、步长为$4$的过滤器输入,激活函数为非线性整流器。第二个隐层$324\times4$尺寸的、步长为$2$的过滤器输入,激活函数也是非线性整流器。最后一个隐层是全连接层,由$256$个整流单元构成。输出层由线性层组成,每个输出对应一个单独的动作。在不同的游戏中,动作范围在$4$到$18$间发生改变。 我们将我们的卷积神经网络训练方法称为Deep Q-Networks(DQN)。
5 实验
目前,我们在7个受欢迎的雅达利游戏上进行了我们的实验:Beam Rider,Breakout,Enduro,Pong,Q*bert,Seaquest,,Space Invaders。在七个游戏中,我们使用了相同的网络结构、学习算法和超参数设置。我们的方法在不同的游戏上具有足够的鲁棒性,无需配合游戏的额外信息。当我们需要让智能体在真实的、固定的游戏上迭代时,我们只做了一个改变,就是对游戏奖励的设置,并且只在训练时进行了改动。 考虑到游戏间分数机制差别很大,我们将所有积极的奖励值设置为了$1$,所有不积极的奖励值设置为了$-1$,其他的所有奖励都是$0$。 如此设置奖励值,可以对意想不到的错误进行限制,并且让学习率可以适用于不同的游戏。与此同时,这可以影响我们的智能体性能,因为这种情况下奖励的题量没有区分。
在这些实验中,我们使用RMSProp的优化算法,训练的批量(mini-batch)为$32$。 训练中,行为策略使用贪婪策略,其中$\epsilon$在前100万步中从1到0.1线性递减,并最终在0.1处固定。我们训练了总共1000万步,经验池大小为100万。
使用上述方法操控雅达利游戏外, 我们还使用了一个简单的帧跳跃的技术。更准确地说,智能体在每$k$步才观察并选择帧图像,而非每一步。 智能体最近一次选择的动作在其跳过的帧上重复。这个技术时考虑到了模拟器进行步进比智能体选择动作需要更少的计算资源,因此这个技术可以让智能体在同样的运算时间下比正常情况多玩大概k次游戏。除了Space Invaders外,我们为所有游戏设置了$k=4$;在Space Invaders中,我们注意到$k=4$会让激光器因为其持续在blink状态而变得不可见。我们使用$k=3$来让激光器可见,而这只会在游戏间造成了很小的超参数改变。
5.1 训练和稳定性
在监督学习中,我们可以很轻易地通过模型在训练集与测试集上的评估效果对模型表现进行追踪。在强化学习中,对训练中的智能体进行精准评价是具有挑战性的。我们的根据[Marc G Bellemare, Yavar Naddaf, Joel Veness, and Michael Bowling. The arcade learning environment: An evaluation platform for general agents. Journal of Artificial Intelligence Research, 47:253–279, 2013.]构建了评判指标,该指标是智能体在一幕游戏或者游戏平均值下生成的总回报,我们在训练时定期对其进行计算。平均总回报这个指标看起来很不稳定,因为在策略上一个小的权重改变就能导致状态分布发生巨大的变化。图2的左边两个子图显示了训练Seaquest和Breakout游戏时平均总回报的变化。这两个平均回报确实十分不稳定,看起来这个学习算法可能不是一个稳定的过程。而另一个更加稳定的指标是策略对于动作价值的估值$Q$函数,这个函数用于估计在任何状态下,以当前的策略智能体可以获得多少折扣后的奖励。我们通过在训练开始前基于随机策略收集了一组固定的状态集,并且基于这个状态集,收集了随着训练进行这些状态对应的最优动作的平均价值。在图2最右侧的两个子图中可以看出,平均动作估值的上升相比于平均总奖励值平滑得多。在其他5个游戏中也是如此。 此外,我们观测到我们进行的与$Q$估值平滑有关的改进,并没有在实验中造成不收敛的情况。这表明了,尽管缺少理论收敛的基础,但是我们能够通过使用强化学习特征与随机梯度下降的方法稳定地训练一个大型神经网络。
5.2 价值函数可视化
图3展示了Seaquest游戏中价值的可视化。 图像显示当一个敌人从屏幕左侧出现(A点),预估价值突然提升。智能体随后对这个敌人进行鱼雷攻击,此时预估价值达到峰值(B点)。最后,当这个敌人消失时,价值大幅度下降(C点)。 图3描述了我们的方法能够观测到价值函数是如何随着合理化的事件序列而变化的。
5.3 主要评价
我们将我们的结果与强化学习文献中那些表现最好的方法进行比较。Sarsa方法使用了Sarsa算法在几个不同的人工的特征集合上学习线性策略,其在雅达利任务上进行学习,而我们的方法在这个特征集上取得了最好的表现成绩。Contingency方法与Sarsa方法使用了同样的基础方案,但是通过一种智能体控制的方法来扩充特征集合。注意到这两个方法都结合了视觉问题中的先验知识,通过使用背景预处理并将128个颜色分别视为单独的通道。由于许多雅达利游戏为每种类型的对象使用了一种不同的颜色,因此将每种颜色作为一个单独的通道类似于为每种对象都生成一个单独的二进制映射编码。相反,我们的智能体只接收未处理的RGB截屏输入,而其必须依靠自己学习检测物体。
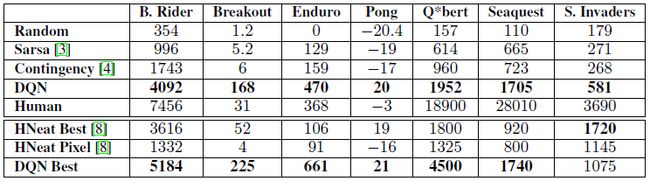
除了记录我们的智能体的数据,我们也记录了人类专家与随机动作选取的表现。人类玩家的表现在他们玩完每个游戏各2个小时后记录奖励的平均值。 注意我们的人类玩家得分比Bellemare等人记录的高很多。 对于我们训练的智能体,我们遵照Bellemare的迭代策略,并且记录了在$\epsilon=0.05$贪婪策略下,固定步数的平均得分。在表1的前五行中,显示了所有游戏的平均得分。我们的方法(在表格中是DQN)在七个游戏的表现比其他学习方法表现都好很多,并且还是在几乎没有对输入进行先验处理的情况下。
我们还考虑了与[Matthew Hausknecht, Risto Miikkulainen, and Peter Stone. A neuro-evolution approach to general atari game playing. 2013.]工作中的进化策略搜索方法相比较,记录在表1的最后三行中。我们为这个工作记录了两个结果集合。其中HNeat Best反映了使用人工检验对象位置与对象类型算法的结果。而HNeat Pixel反映了使用8个颜色通道来进行对象归类的算法效果。
这种方法在很大程度上依赖于找到一个成功利用了漏洞的序列。以这种方式进行学习不太可能推广到随机扰动的情况下。因此,我们只取最高得分的幕进行算法评估。相反,我们的算法是在贪婪控制序列上进行评估的,因此能够在各种评估方式下进行评估。 最终,我们发现,除了Space Invaders,我们的算法在最优分数(第8行)与平均结果(第4行)上都能取得最好的性能。 (Piper蛋窝批注:真正有底气的科研,并不需要尬吹自己在一切实验上表现都很好,这里, DQN 在 Space Invade 上结果就不是最优的)
最后,我们的算法在Breakout,Enduro与Pong游戏上获得了比人类专家更好的表现,在Beam Rider上接近人类表现。Q*bert,Seaquest,Space Invaders这三个游戏比人类的表现差的很远,控制好这三个游戏更加具有挑战性,因为他们需要网络模型去寻找一个长时效性的策略。
6 结论
本文介绍了一个新的基于强化学习的深度学习模型,并且描述了其在只有未处理像素输入下,对于雅达利2600电子游戏的强大控制力。我们提出了一个在线Q-learning的变体,结合了基于经验池技术的随机小批量更新来轻量地训练强化学习的深度网络。无需调整超参数,我们的方法为测试的六个游戏提供了SOTA级别的结果。
感谢你读到最后!我是小拍,一名计算机技术爱好者!觉得文章不错的话,可以点击“在看”支持我一下!有任何批评建议或者合作事宜,可以给我发邮件 [email protected] ,或者关注公众Piper蛋窝,回复「微信」来加我微信联系~