第三章 matlab绘图
- 第三章 matlab绘图
- 一.二维数据曲线的绘制
- 1.单独二维曲线的绘制
- 2.多根二维曲线的绘制
- 1)plot函数的输入参数是矩阵形式
- 2)含多个输入参数的plot的函数
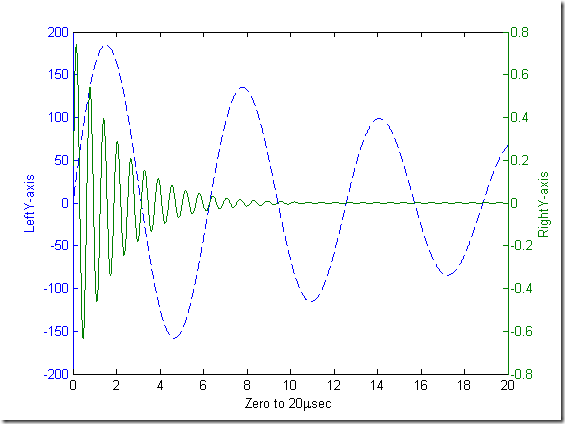
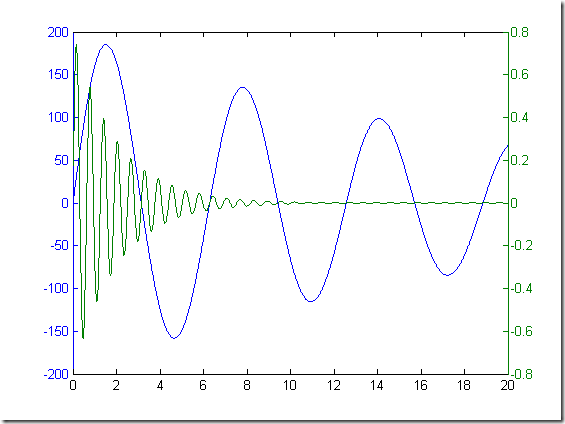
- 3)plotyy函数[AX,H1,H2] = plotyy(x1,y2,x2,y2,'function')
- 3.设置曲线样式 | 颜色,线型,标记符号.
- 4.图形的标注与坐标控制
- 1)图形的标注
- 2)坐标控制
- 5.图形窗口的分割
- 二.其他二维图形的绘制
- 1.特殊坐标图形
- 1)绘制对数坐标图形
- 2)绘制极坐标图形
- 2.特殊二维图形的绘制
- 1)条形图的绘制 bar
- 2)面积图的绘制area
- 3)饼图的绘制pie pie3
- 4)火柴杆图的绘制stem
- 5)矢量图的绘制
- 6)绘制等高线contour
- 为了节约内存,这里运行完成程序后清空.
clc; clear all; close all;
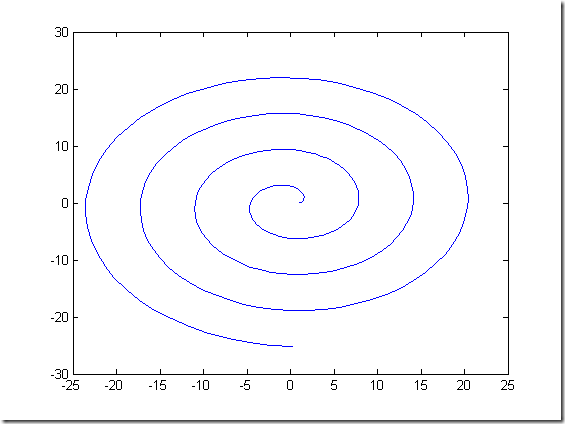
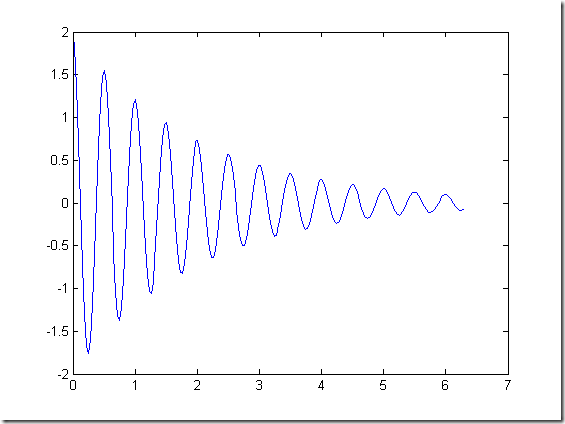
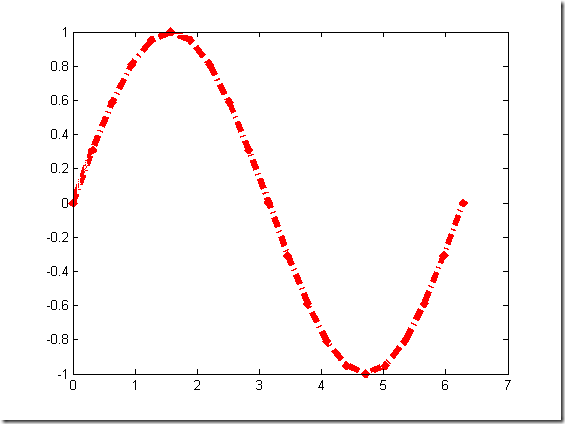
% plot(x,y) % % 在0<=x<=2*pi区间内,绘制曲线y=2*exp(-0.5*x)*cos(4*pi*x) x = 0:pi/100:2*pi; y =2*exp(-0.5*x).*cos(4*pi*x); figure; plot(x,y) % % 绘制曲线x = cost+tsint y = sint -tcost t = 0:0.1:8*pi; x = cos(t)+t.*sin(t); y = sin(t)-t.*cos(t); figure plot(x,y)
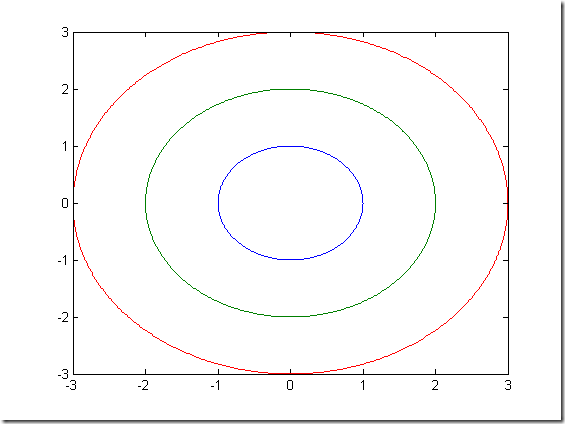
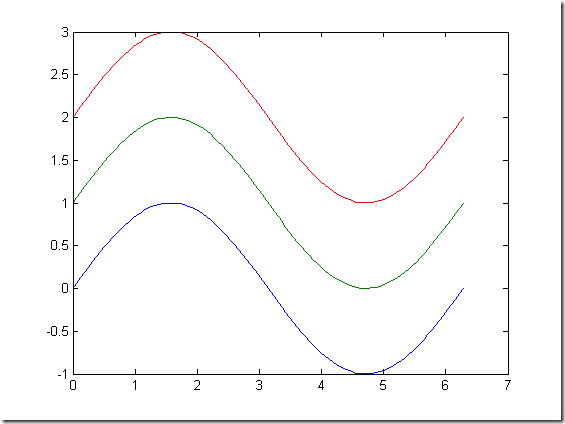
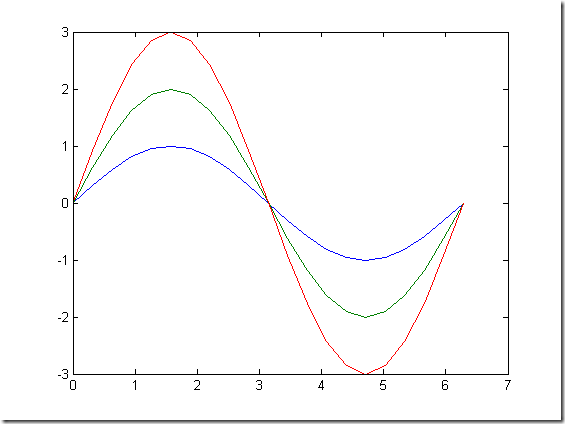
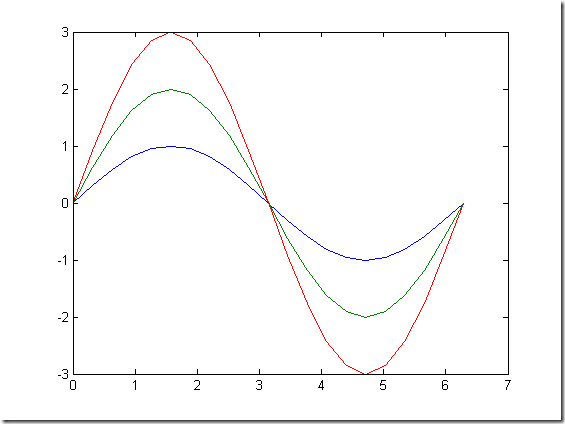
% % 当x是向量时,y是也有一维与x同维的矩阵时. x = linspace(0,2*pi,100); y =[sin(x);1+sin(x);2+sin(x)]; figure plot(x,y) % %x,y是同维矩阵. x = 0:pi/10:2*pi; y = sin(x); figure plot([x;x;x]',[y;y*2;y*3]') % %当输入参数是实矩阵时,则按列绘制没列元素值相对于其坐标下的曲线. t = 0:0.01:2*pi; x = exp(i*t); y = [x;x*2;x*3]'; figure plot(y)
% %当plot函数有多个输入参数,每两个组成一组.
x = 0:pi/10:2*pi;
y = sin(x);
figure
plot(x,y,x,y*2,x,y*3)
% 格式 : % plotyy(x1,y1,x2,y2) % plotyy(x1,y2,x2,y2,'function') % [AX,H1,H2] = plotyy(x1,y2,x2,y2,'function') % % 使用函数plotyy绘制两个数学函数 x = 0:0.01:20; y1 = 200*exp(-0.05*x).*sin(x); y2 = 0.8*exp(-0.5*x).*sin(10*x); figure [AX,H1,H2] = plotyy(x,y1,x,y2,'plot'); % % 添加样式x = 0:0.01:20; y1 = 200*exp(-0.05*x).*sin(x); y2 = 0.8*exp(-0.5*x).*sin(10*x); figure [AX,H1,H2] = plotyy(x,y1,x,y2,'plot'); set(get(AX(1),'Ylabel'),'String','LeftY-axis'); % AX(1)是左侧的y轴 set(get(AX(2),'Ylabel'),'String','RightY-axis'); % AX(2)是右侧的y轴 xlabel('Zero to 20\musec'); % 添加x轴的标签 set(H1,'LineStyle','--'); % H1所代表的曲线. set(H2,'LineStyle','-'); % H2所代表的曲线.
% %-------------------- % 颜色选项 颜色 % b(blue) 蓝色 % g(green) 绿色 % r(red) 红色 % c(cyan) 青色 % m(magenta) 品红色 % y(yellow) 黄色 % b(black) 黑色 % w(white) 白色 % %-------------------- % 线型选项 线型 % - 实线 % : 虚线 % -. 点划线 % -- 双划线 % %-------------------- % 选项 标记符号 % . 点 % O 圆圈 % X 叉号 % + 加号 % * 星号 % s(square) 方块符 % d(diamond) 菱形符 % v 朝下三角符号 % ^ 朝上三角符号 % < 朝左三角符号 % > 朝右三角符号 % p(pentagram) 五角星符 % h(hexagram) 六角星符 % % 以线宽5,红色,点画线,叉号形式绘画x在[0,2*pi]内的正弦函数y=sin(x)的图形. x = 0:pi/10:2*pi; y = sin(x); figure plot(x,y,'r-.X','LineWidth',5);
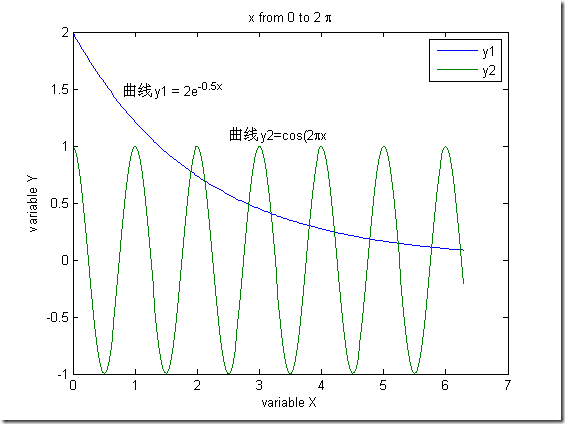
% title(s) 书写图名 % xlabel(s) 横坐标轴名 % ylabel(s) 纵坐标轴名 % legend(s1,s2) 绘制曲线的图例 % text(xt,yt,s) 在图里(xt,yt)坐标处书写字符注释. % %---------------常用的LaTeX字符--------------------- % \alpha α \upsilon υ \sim ~ % \beta β \phi ? \leq ≤ % \gamma γ \chi χ \infty ∞ % \delta δ \psi ψ \clubsuit % \epsilon ? \omega ω \diamondsuit % \zeta ζ \Gamma Γ \heartsuit % \eta η \Delta Δ \spadesuit % \theta θ \Theta Θ \leftrightarrow ? % \vartheta ? \Lambda Λ \leftarrow ← % \iota ι \Xi Ξ \uparrow ↑ % \kappa κ \Pi Π \rightarrow → % \lambda λ \Sigma Σ \downarrow ↓ % \mu μ \Upsilon Υ \circ ° % \nu ν \Phi Φ \pm ± % \xi ξ \Psi Ψ \geq ≥ % \pi π \Omega Ω \propto ∝ % \rho ρ \forall ? \partial ? % \sigma σ \exists ? \bullet ? % \varsigma ? \ni % \div ÷ % \tau τ \cong ? \neq ≠ % \equiv ≡ \approx ≈ \aleph ? % \Im % \Re % \wp % \otimes ? \oplus ? \oslash % \cap ∩ \cup ∪ \supseteq ? % \supset ? \subseteq ? \subset ? % \int ∫ \in ∈ \o ο % \rfloor % \lceil % \nabla % \lfloor % \cdot % \ldots % \perp % \neg % \prime % \wedge % \times % \0 ? % \rceil % \surd % \mid | % \vee % \varpi % \copyright ? % \langle % \rangle % % 在0,2pi区间,绘制曲线y1= 2exp(-0.5x)和y2=cos(2*pi*x),并给图形添加标注. x = 0:pi/100:2*pi; y1=2*exp(-0.5*x); y2 = cos(2*pi*x); figure plot(x,y1,x,y2) title('x from 0 to 2 {\pi}') xlabel('variable X') ylabel('variable Y') text(0.8,1.5,'曲线y1 = 2e^{-0.5x}') text(2.5,1.1,'曲线y2=cos(2{\pi}x') legend('y1','y2')
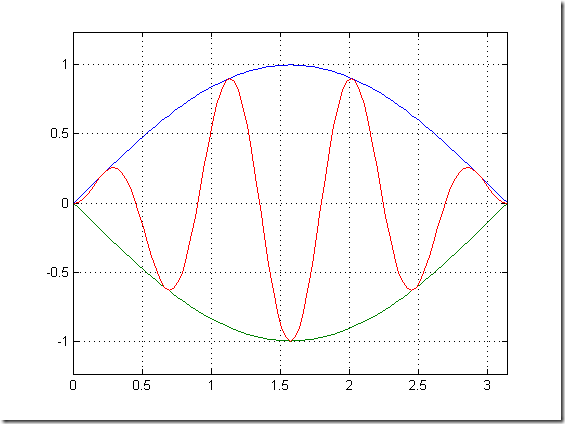
% % axis([xmin xmax ymin ymax]) % %--------------------------------------------- % % 在0,4pi区间内,画出正弦波在y轴介于0和1的部分. x =0:0.1:4*pi; y = sin(x); plot(x,y) axis([-inf inf 0 1]) % %--------------------------------------------- % % 绘制曲线y=sintsin(7t)及其包络线. t = (0:pi/100:pi)'; y1 = sin(t)*[1,-1]; y2 = sin(t).*sin(7*t); figure plot (t,[y1,y2]'); grid on box on axis equal
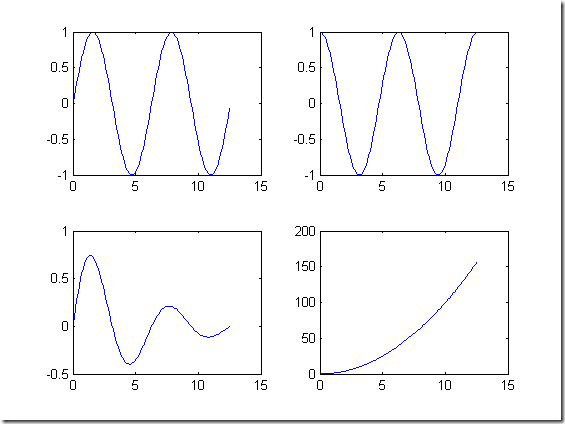
% % subplot(m,n,p) m行n列的第p个绘图区域. % %--------------------------------------------- % %在一个窗口中同时绘制出4个图形. x = 0:0.1:4*pi; subplot(2,2,1); plot(x,sin(x)) %此为左上角图形. subplot(2,2,2); plot(x,cos(x)) %此为右上角图形. subplot(2,2,3); plot(x,sin(x).*exp(-x/5)) %此为左下角图形. subplot(2,2,4); plot(x,x.^2) %此为右下角图形.
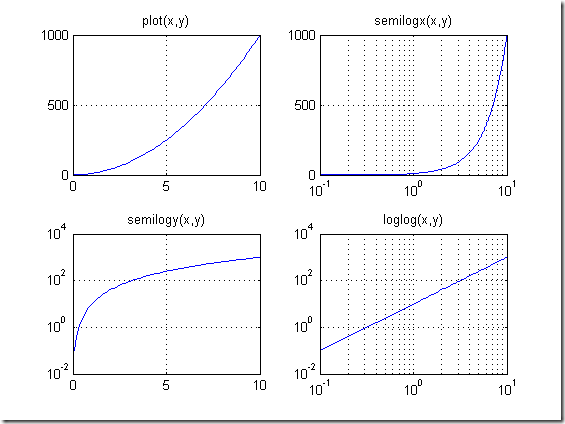
% % semilogx(x1,y1,选项1,x2,y2,选项2...) % % semilogy(x1,y1,选项1,x2,y2,选项2...) % %loglog(x1,y1,选项1,x2,y2,选项2...) % %--------------------------------------------- % %绘制y=10*x*x的对数座标图形和指教线性坐标图形. x = 0:0.1:10; y = 10*x.*x; figure subplot(2,2,1) plot(x,y) title('plot(x,y)') grid on subplot(2,2,2) semilogx(x,y); title('semilogx(x,y)') grid on subplot(2,2,3) semilogy(x,y); title('semilogy(x,y)') grid on subplot(2,2,4) loglog(x,y); title('loglog(x,y)') grid on
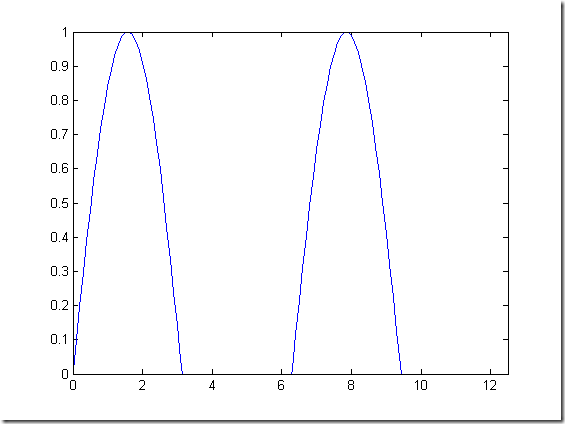
% %polar(t,r,option) % % t角度 % % r幅度向量 % % option选项. % %--------------------------------------------- % %绘制y=2sin(2t-pi/4)cos(2t-pi/4)的极坐标图形,并标注数据点. t = 0:0.01:2*pi; r = 2*sin(2*(t-pi/8)).*cos(2*(t-pi/8)); figure polar(t,r)
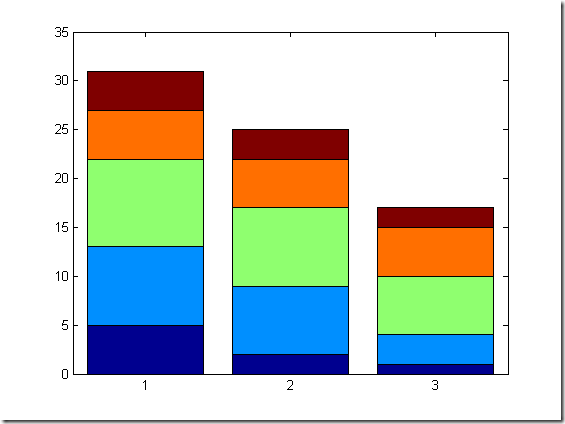
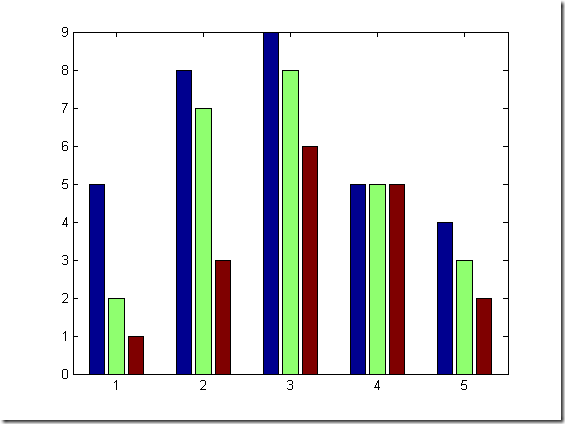
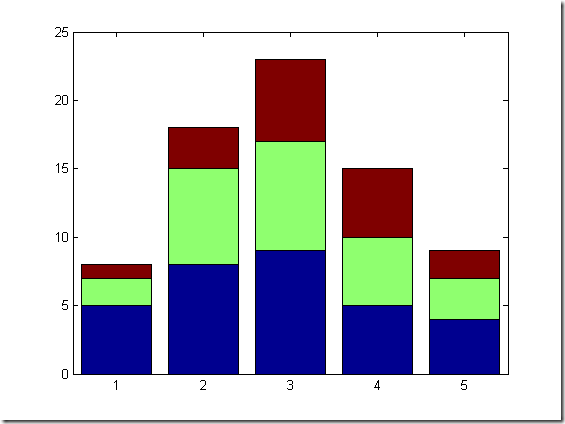
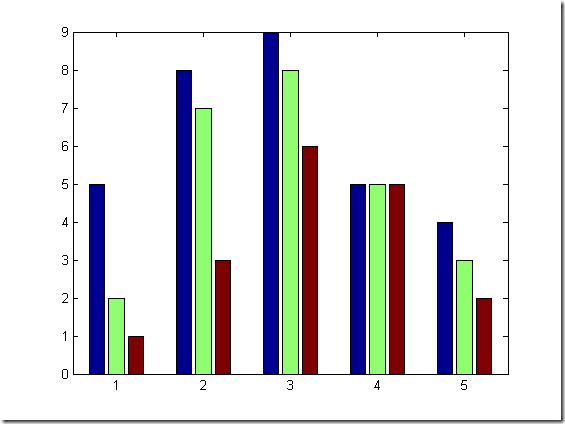
% bar(y,option) 以x=1,2,3...为x坐标,y的对应元素为y坐标画垂直放置的二维条形图 % bar(x,y,option) 以x各个元素为x坐标,y的对应元素为y坐标画垂直放置的二维条形图 % bar(y,'stack') 以x=1,2,3...为x坐标,y的各[行]元素为累加值为y坐标. % bar(y,'group') 以x=1,2,3...为x坐标,y的各[列]元素的累加值为y坐标. % %--------------------------------------------- % %用给定的数据绘制二维条形图 Y=[5 2 1;8 7 3; 9 8 6;5 5 5 ;4 3 2]; bar(Y) figure bar(Y,'stack') figure bar(Y,'group') %似乎group不对头.... figure bar(Y','stack')
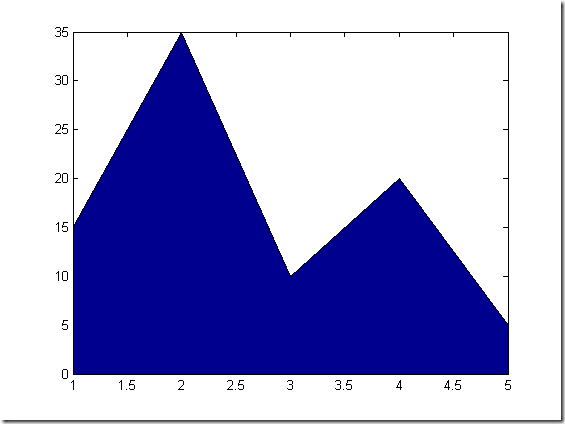
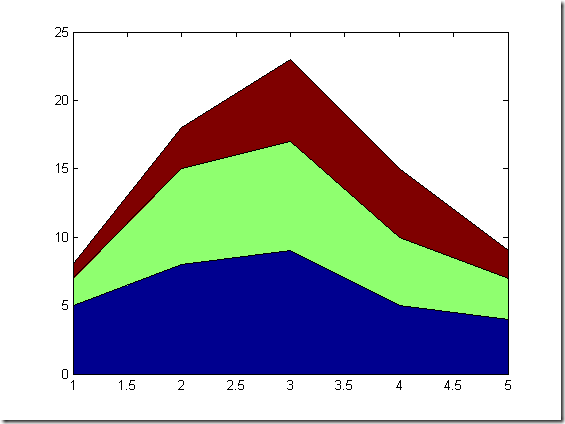
% %area(y) 以x=1,2,3...为x坐标,y的对应元素为y坐标画二维折线图,并填充与x轴的区域. % %area(x,y) 以x各个元素为x坐标,y的对应元素为y坐标画二维折线图,并填充与x轴的区域. y = [15,35,10,20,5]; area(y) Y=[5 2 1;8 7 3; 9 8 6;5 5 5 ;4 3 2]; figure area(Y) %以Y的每一列y为一组值画图.
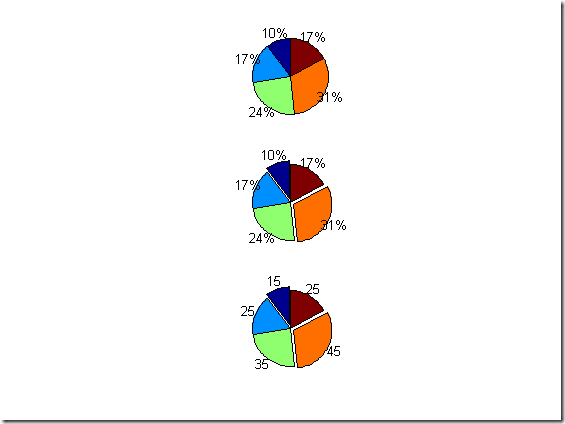
% %pie(y) 绘制每一元素占全部向量元素的总和值的百分比. % %pie(y,explode) explode为与y同维的0,1向量,非0表示对应y元素从饼图中分离出来. % % pie3 绘制3维饼图. y = [ 15 25 35 45 25 ] figure subplot(3,1,1) pie(y) subplot(3,1,2) pie(y,[1 0 0 1 0 ]) subplot(3,1,3) pie(y,[1 0 0 1 0 ],{'15','25','35','45','25'})
y =
15 25 35 45 25
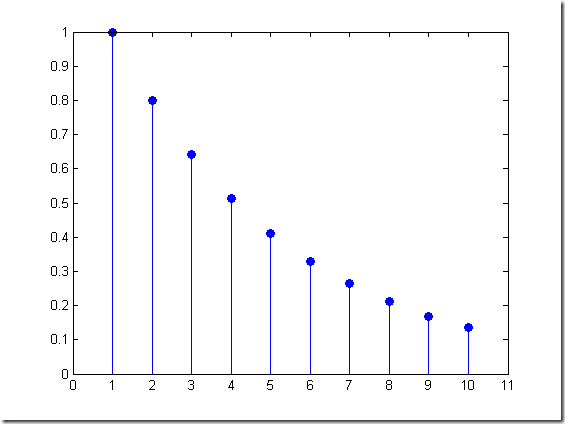
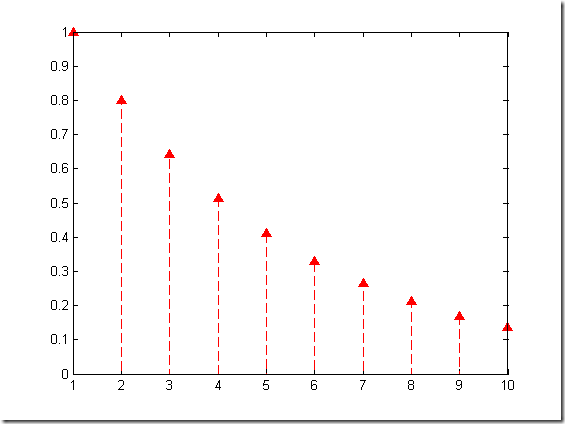
% %stem(y) % %stem(x,y,option) % %stem(x,y,'filled') % %--------------------------------------------- y = linspace(0,2,10) figure stem(exp(-y),'filled') axis([0 11 0 1]) figure stem(exp(-y),'filled','r--^') % 实际使用的是 stem(y,'filled',option) % 其中option为线型,线颜色,点型,点颜色.
y =
0 0.2222 0.4444 0.6667 0.8889 1.1111 1.3333 1.5556 1.7778 2.0000
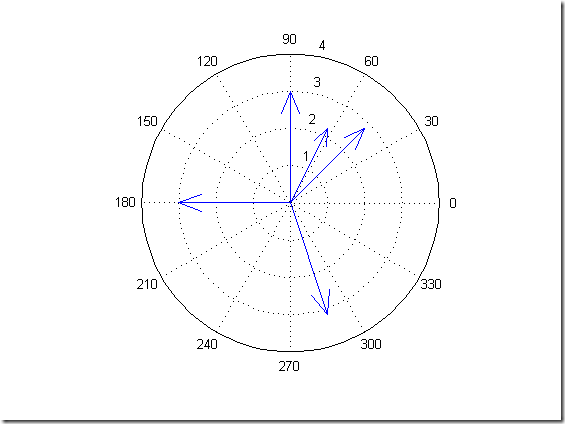
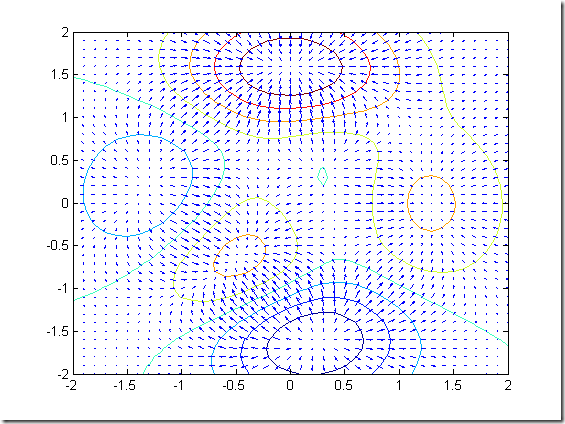
% compass 绘制从源极点散发的矢量 % feather 从一个水平直线等间距出发,图形显示矢量. % quiver 显示2D矢量场. % %--------------------------------------------- z = [1+2j 2+2j 1-3j 3j -3] figure compass(z) figure feather(z) grid on % %--------------------------------------------- % % 【预备知识】 % % FX = gradient(F) % 其中F是一个向量。该格式返回F的一维数值梯度。FX即?F/?x,即沿着x轴(水平轴)方向的导数。 % [FX,FY] = gradient(F) % 其中F是一个矩阵。该调用返回二维数值梯度的x、y部分。FX对应?F/?x, FY对应于?F/?y。 % [FX,FY,FZ,...] = gradient(F) % 这里,F是一个含有N个自变量的多元函数。 % [...] = gradient(F,h) % 这里的h指定了沿着梯度的方向取点的间隔。 % [...] = gradient(F,h1,h2,...) % % contour(X,Y,Z), contour(X,Y,Z,n), and contour(X,Y,Z,v) draw contour plots % of Z使用Z来画等高线 % using X and Y to determine the x- and y-axis limits. X和Y用来定X,Y的限制. % When X and Y are matrices, % they must be the same size as Z and must be monotonically increasing. % % 【预备知识】 % % [X,Y,Z] = peaks(n); %返回Z为高斯分布的离散值.X,Y为画三维曲线在xoy平面的投影区域 % % 使用quiver命令画一个矢量场 n= -2.0:0.1:2.0; [X,Y,Z] = peaks(n); %返回Z为高斯分布的离散值.X,Y为画三维曲线在xoy平面的投影区域 contour(X,Y,Z,8); %1.绘制等高线,等高线分8条等高. hold on [Zx,Zy]= gradient(Z,0.2); %平均0.2间隔采样曲面Z,然后求点处的梯度. quiver(X,Y,Zx,Zy); %2.在点(x,y)处绘制向量(Zx,Zy) hold off
z = 1.0000 + 2.0000i 2.0000 + 2.0000i 1.0000 - 3.0000i 0 + 3.0000i -3.0000
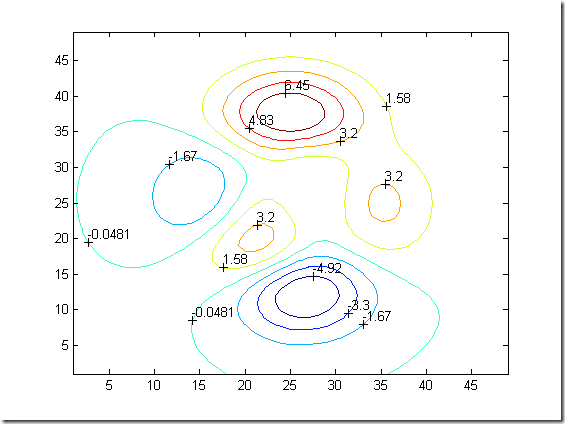
% contour(Z) 绘制矩阵Z的等值线图. % contour(Z,n) 绘制n个等值水平的Z矩阵的等值线图 % c=contourc(Z,n) 计算等高线的坐标 % clable(c) 给等高线加标注. % %----------------------------------- % % 在二维平面上绘制peaks函数的8条等高线. contour(peaks,8) %绘制peaks函数的8条等高线 c = contourc(peaks,8); %计算等高线坐标 clabel(c) %添加等高线标注. % n= -2.0:0.1:2.0; % Z = peaks(n); % contour(Z,8) % c = contourc(peaks,8); % clabel(c)
clear
close all
clc