轮胎的魔术公式(Magic Fomula)模型

本篇结合Adams中的TR_rear_pac89.tir文件，介绍一下魔术公式的基本知识。使用魔术公式的轮胎模型主要有Pacejka ’89、Pacejka ’94、MF-Tyre、MF-Swift四种。

 

1. Pacejka ’89和’94轮胎模型

Pacejka ’89 和’94轮胎模型是以魔术公式主要提出者H. B. Pacejka教授命名的，根据其发布的年限命名。目前有两种直接被ADAMS引用。

魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式就可以完整地表达轮胎的纵向力F_x、侧向力F_y、回正力矩M_z、翻转力矩M_x、阻力矩M_y以及纵向力、侧向力的联合作用工况，故称为“魔术公式”。

魔术公式的一般表达式为：

式中Y(x)可以是侧向力，也可以是回正力矩或者纵向力，自变量x可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率，式中的系数B、C、D依次由轮胎的垂直载荷和外倾角来确定。

Pacejka ’89轮胎模型认为轮胎在垂直、侧向方向上是线性的、阻尼为常量，这在侧向加速度常见范围≤0.4g，侧偏角≤5°的情景下对常规轮胎具有很高的拟合精度。此外，由于魔术公式基于试验数据，除在试验范围的高精度外，甚至在极限值以外一定程度仍可使用，可以对有限工况进行外推且具有较好的置信度。魔术公式正在成为工业标准，即轮胎制造商向整车厂提供魔术公式系数表示的轮胎数据，而不再是表格或图形。

基于魔术公式的轮胎模型还有较好的健壮性，如果没有某一轮胎的试验数据，而使用同类轮胎数据替代仍可取得很好的效果。

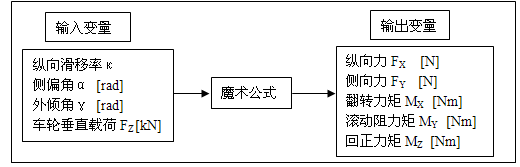
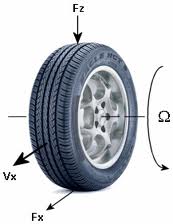
图 基于魔术公式的轮胎模型的输入和输出变量

Pacejka ’89轮胎力与力矩的计算

轮胎纵向力计算公式为：

其中X₁为纵向力组合自变量：X₁=(κ+S_h)，κ为纵向滑移率（负值出现在制动态，-100表示车轮抱死）

C——曲线形状因子，纵向力计算时取B₀值：C = B₀

D——巅因子，表示曲线的最大值：

BCD——纵向力零点处的纵向刚度：

B – 刚度因子：B=BCD/(C×D)

S_h——曲线的水平方向漂移：

S_v——曲线的垂直方向漂移：S_v=0

E——曲线曲率因子，表示曲线最大值附近的形状：

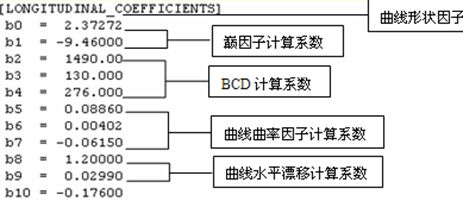
图 轮胎属性文件中的纵向力计算系数数据块

 

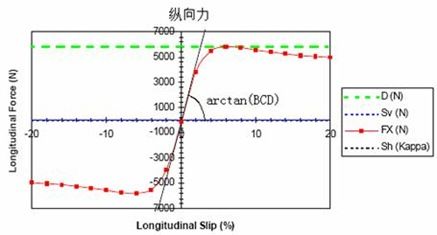
图 Pacejka ’89轮胎纵向力示例

 

轮胎侧向力计算公式为：

此时的X₁为侧向力计算组合自变量：X₁=(α+S_h)，α为侧偏角

C——曲线形状因子，侧向力计算时取A₀值：C = A₀

D——巅因子，表示曲线的最大值：

BCD——侧向力零点处的侧向刚度：

B – 刚度因子：B=BCD/(C×D)

S_h——曲线的水平方向漂移：

S_v——曲线的垂直方向漂移：

E——曲线曲率因子，表示曲线最大值附近的形状：

 

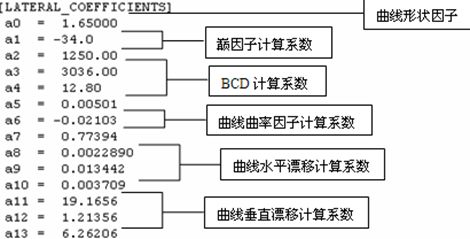
图 轮胎属性文件中的侧向力计算系数数据块

 

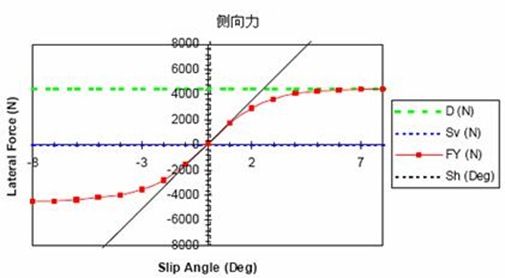
图 Pacejka ’89轮胎纵向力示例

 

轮胎回正力矩计算公式为：

此时的X₁为回正力矩计算组合自变量：X₁=(α+S_h)，α为侧偏角

C——曲线形状因子，回正力矩计算时取C₀值：C = C₀

D——巅因子，表示曲线的最大值：

BCD——回正力矩零点处的扭转刚度：

B – 刚度因子：B=BCD/(C×D)

S_h——曲线的水平方向漂移：

S_v——曲线的垂直方向漂移：

E——曲线曲率因子，表示曲线最大值附近的形状：

 

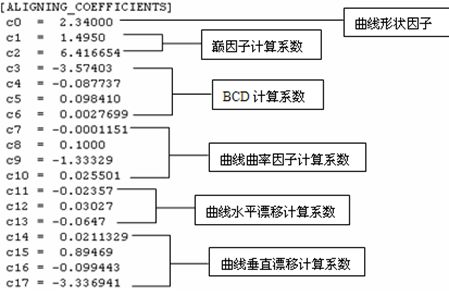
图 轮胎属性文件中的回正力矩计算系数数据块

 

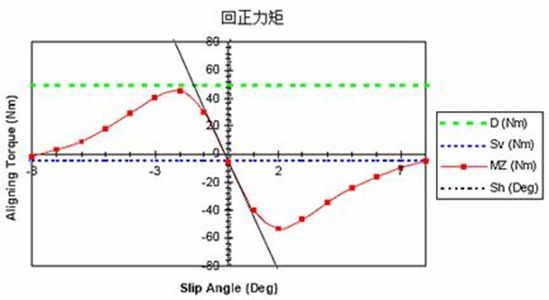
图 Pacejka ’89轮胎回正力矩示例

 

侧偏刚度（Lateral Stiffness）

侧偏刚度在Pacejka ’89和’94轮胎模型中假定是一个常量，在轮胎属性文件的参数PARAMETER数据段中通过LATERAL_STIFFNESS语句设定。

侧向形变D_e：D_e＝Fy /LATERAL_STIFFNESS；

翻转力矩：Mx ＝ -F_z ×D_e；

纵向力和侧偏角联合作用的回正力矩Mz；

M_Z = M_Z,MF + Fx×D_e ，这里M_Z,MF为魔术公式计算所得的回正力矩。

滚动阻力（Rolling resistance）

滚动阻力系数R_R同样是在轮胎属性文件中规定的具体值，滚动阻力矩My：

My = Fz ×R_e×R_R

这里：R_e为轮胎的滚动半径；R_R为滚动阻力系数；Fz垂直载荷（kN）。

平滑过渡（Smoothing）

是否使用平滑过渡也在轮胎属性文件中规定：

² USE_MODE = 1 或 2：关闭平滑过渡

² USE_MODE = 3 或 4：使用平滑过渡

轮胎属性文件TR_rear_pac89.tir全文（示例整车模型MDI_Demo_Vehicle.asy使用的）：

$---------------------------------------------------------------------MDI_HEADER

[MDI_HEADER]

FILE_TYPE = 'tir'

FILE_VERSION = 2.0

FILE_FORMAT = 'ASCII'

(COMMENTS)

{comment_string}

'Tire - XXXXXX'

'Pressure - XXXXXX'

'Test Date - XXXXXX'

'Test tire'

'New File Format v2.1'

$--------------------------------------------------------------------------UNITS

[UNITS]

LENGTH = 'mm'

FORCE = 'newton'

ANGLE = 'radians'

MASS = 'kg'

TIME = 'sec'

$--------------------------------------------------------------------------MODEL

[MODEL]

! use mode 1 2 3 4

! -------------------------------------------

! smoothing X X

! combined X X

!

PROPERTY_FILE_FORMAT = 'PAC89' 轮胎模型关键词

FUNCTION_NAME = 'TYR900' 解算器函数

USE_MODE = 4.0 平滑过渡模式

$----------------------------------------------------------------------DIMENSION

[DIMENSION]

UNLOADED_RADIUS = 340.6 轮胎自由半径

WIDTH = 255.0 轮胎宽度

ASPECT_RATIO = 0.35 高宽比

$----------------------------------------------------------------------PARAMETER

[PARAMETER]

VERTICAL_STIFFNESS = 310.0 纵向刚度系数

VERTICAL_DAMPING = 3.1 纵向阻尼系数

LATERAL_STIFFNESS = 190.0 侧偏刚度

ROLLING_RESISTANCE = 0.0 滚动阻力系数

$-----------------------------------------------------------LATERAL_COEFFICIENTS

[LATERAL_COEFFICIENTS]

a0 = 1.65000

a1 = -34.0

a2 = 1250.00

a3 = 3036.00

a4 = 12.80

a5 = 0.00501

a6 = -0.02103

a7 = 0.77394

a8 = 0.0022890

a9 = 0.013442

a10 = 0.003709

a11 = 19.1656

a12 = 1.21356

a13 = 6.26206

$-------------------------------------------------------------------longitudinal

[LONGITUDINAL_COEFFICIENTS]

b0 = 2.37272

b1 = -9.46000

b2 = 1490.00

b3 = 130.000

b4 = 276.000

b5 = 0.08860

b6 = 0.00402

b7 = -0.06150

b8 = 1.20000

b9 = 0.02990

b10 = -0.17600

$----------------------------------------------------------------------aligning

[ALIGNING_COEFFICIENTS]

c0 = 2.34000

c1 = 1.4950

c2 = 6.416654

c3 = -3.57403

c4 = -0.087737

c5 = 0.098410

c6 = 0.0027699

c7 = -0.0001151

c8 = 0.1000

c9 = -1.33329

c10 = 0.025501

c11 = -0.02357

c12 = 0.03027

c13 = -0.0647

c14 = 0.0211329

c15 = 0.89469

c16 = -0.099443

c17 = -3.336941

注意：属性文件中的单位数据块[UNITS]不用于魔术公式的系数a,b,c。

 

2. 代码

MF5.2的实现代码：

void RPacejka::CalcMF52()

// Pacejka MF5.2 (~2006)

{

   rfloat Fx0,Dx,Cx,Ex,Bx,dfz,Fz0,Fz0_der;             // Nominal load, adapted nominal load

   rfloat kx,k,mux,sign_kx;

   rfloat Shx,Svx,Kx,gamma,gamma_x;

   rfloat Fzn;                     // Fz in Newtons

   rfloat tmp;



   //

   // Global

   //

   k=slipPercentage*0.01f;   // Slip ratio

   Fzn=Fz*1000.0f;

   Fz0=fz0; //4500;

   Fz0_der=lfz0*Fz0;

   dfz=(Fzn-Fz0_der)/Fz0_der;

   gamma=camber/RR_RAD2DEG;

   //

   // Fx (pure slip)

   //

   Shx=(phx1+phx2*dfz)*lhx;

   Svx=Fzn*(pvx1+pvx2*dfz)*lvx*lmux;

   kx=k+Shx;

   if(kx<0)sign_kx=-1.0f;

   else    sign_kx=1.0f;



   gamma_x=gamma*lgax;



   Cx=pcx1*lcx;

   mux=(pdx1+pdx2*dfz)*(1.0f-pdx3*gamma_x*gamma_x)*lmux;     // Different in Pac2006

   Ex=(pex1+pex2*dfz+pex3*dfz*dfz)*(1.0f-pex4*sign_kx)*lex;

   // Limiter on Ex (eq 23)

   if(Ex>1.0f)Ex=1.0f;

   Dx=mux*Fzn;

   Kx=Fzn*(pkx1+pkx2*dfz)*expf(pkx3*dfz)*lkx;                // K=BCD (=stiffness)

   // Low velocity trouble

   tmp=Cx*Dx;

   if(fabs(tmp)<0.001f)

   Bx=Kx/(tmp+0.001f);

   else

   Bx=Kx/tmp;



   tmp=Bx*kx;

   Fx0=Dx*sinf(Cx*atanf(tmp-Ex*(tmp-atanf(tmp))))+Svx;



   //

   // Fy

   //

   rfloat Fy0,Dy,Cy,Ey,By;

   rfloat localMuy;

   rfloat Shy,Svy,Ky;

   rfloat say,sign_alpha_y;

   rfloat gamma_y;

   rfloat alpha;



   alpha=sideSlip/RR_RAD2DEG;

   gamma_y=gamma*lgay;



   Cy=pcy1*lcy;

   localMuy=(pdy1+pdy2*dfz)*(1.0f-pdy3*gamma_y*gamma_y)*lmuy;

   Dy=localMuy*Fzn;

   Ky=pky1*Fz0_der*sinf(2.0f*atanf(Fzn/(pky2*Fz0_der)))*(1.0f-pky3*fabs(gamma_y))*lfz0*lky;    // =BCD=stiffness at slipangle 0



   tmp=Cy*Dy;

   if(fabs(tmp)<0.001f)

     By=Ky/(tmp+0.001f);

   else

     By=Ky/tmp;



   Shy=(phy1+phy2*dfz)*lhy+phy3*gamma_y;

   Svy=Fzn*((pvy1+pvy2*dfz)*lvy+(pvy3+pvy4*dfz)*gamma_y)*lmuy;

   say=alpha+Shy;



   if(say<0)sign_alpha_y=-1.0f;

   else     sign_alpha_y=1.0f;

   Ey=(pey1+pey2*dfz)*(1.0f-(pey3+pey4*gamma_y)*sign_alpha_y)*ley;

   // Limiter on Ey (eq 35)

   if(Ey>1.0f)Ey=1.0f;



   // Lateral base force

   tmp=By*say;

   Fy0=Dy*sinf(Cy*atanf(tmp-Ey*(tmp-atan(tmp))))+Svy;



   //

   // Mz

   //

   rfloat Mzr;

   rfloat t0,Dt,Ct,Bt,alpha_t,Et,gamma_z;

   rfloat Sht,Shf;

   rfloat Br,R0;

   rfloat alpha_r,Dr;

   const float lr=1.0f;        // Not found in paper at lambda section



   R0=r0;

   gamma_z=gamma*lgaz;



   Sht=qhz1+qhz2*dfz+(qhz3+qhz4*dfz)*gamma_z;

   alpha_t=alpha+Sht;



   // Avoid division by zero

   if(fabs(Ky)<0.001f)

   if(Ky<0)Ky=-0.001f;

   else    Ky=0.001f;



   Shf=Shy+Svy/Ky;

   alpha_r=alpha+Shf;

   Bt=(qbz1+qbz2*dfz+qbz3*dfz*dfz)*(1.0f+qbz4*gamma_z+qbz5*fabs(gamma_y))*lky/lmuy;    // Pac2006 adds gamma_y^2 dependence (qbz6)

   Ct=qcz1;

   Dt=Fzn*(qdz1+qdz2*dfz)*(1.0f+qdz3*gamma_z+qdz4*gamma_z*gamma_z)*(R0/Fz0_der)*lt;        // lt=lamba_t?



   Et=(qez1+qez2*dfz+qez3*dfz*dfz)*(1.0f+(qez4+qez5*gamma_z)*(2.0f/3.14159265f)*atanf(Bt*Ct*alpha_t));   // <=1

   // Clamp Et (eq 51)

   if(Et>1.0f)Et=1.0f;



   Br=qbz9*lky/lmuy+qbz10*By*Cy;      // Preferred qbz9=0

   tmp=Bt*alpha_t;

   t0=Dt*cosf(Ct*atanf(tmp-Et*(tmp-atan(tmp))))*cosf(alpha);           // t_alpha_t in the paper

   Dr=Fzn*((qdz6+qdz7*dfz)*lr+(qdz8+qdz9*dfz)*gamma_z)*R0*lmuy;        // *cosf(alpha_t) for Pac2006 (in MF52 this is still in Mzr=... below)

   Mzr=Dr*cosf(Ct*atanf(Br*alpha_r))*cos(alpha);                       // last cos(alpha) is cos(alpha_t) in Pac2006



   // No combined aligning moment

   Mz=-t0*Fy0+Mzr;



   //

   // Combined slip

   //

   // Combine (page 30+)

   // Longitudinal

   float Shxa,Exa,Cxa,Bxa,alpha_s,Gxa0,Gxa;

   Shxa=rhx1;

   Exa=rex1+rex2*dfz;

   Cxa=rcx1;

   Bxa=rbx1*cosf(atan(rbx2*k))*lxal;   // +rbx3*gammaStar*gammaStar) (Pac2006)

   alpha_s=alpha+Shxa;

   Gxa0=cos(Cxa*atan(Bxa*Shxa-Exa*(Bxa*Shxa-atan(Bxa*Shxa))));

   if(fabs(Gxa0)>D3_EPSILON)

   Gxa=cos(Cxa*atan(Bxa*alpha_s-Exa*(Bxa*alpha_s-atan(Bxa*alpha_s))))/Gxa0;

   else

   Gxa=0;        // Or 1 for super grip?

   Fx=Gxa*Fx0;



   // Lateral

   float Dvyk,Svyk,Shyk,Eyk,Cyk,Byk,ks,Gyk0,Gyk;



   Dvyk=muy*Fz*(rvy1+rvy2*dfz+rvy3*gamma)*cosf(atanf(rvy4*alpha));

   Svyk=Dvyk*sin(rvy5*atan(rvy6*k))*lvyka;

   Shyk=rhy1+rhy2*dfz;

   Eyk=rey1+rey2*dfz;

   Cyk=rcy1;

   Byk=rby1*cosf(atanf(rby2*(alpha-rby3)))*lyka;

   ks=k+Shyk;

   Gyk0=cosf(Cyk*atanf(Byk*Shyk-Eyk*(Byk*Shyk-atanf(Byk*Shyk))));

   Gyk=cosf(Cyk*atanf(Byk*ks-Eyk*(Byk*ks-atanf(Byk*ks))))/Gyk0;



   Fy=Gyk*Fy0+Svyk;



   // Aligning torque

   float alpha_r_eq,alpha_t_eq,Mzr,Fy_der;

   float sign_alpha_t,sign_alpha_r;

   float kk,s,t;



   if(alpha_t>=0)sign_alpha_t=1.0f;

   else          sign_alpha_t=-1.0f;

   if(alpha_r>=0)sign_alpha_r=1.0f;

   else          sign_alpha_r=-1.0f;

   kk=Kx/Ky;

   kk=(kk*kk*k*k);     // kk^2*k^2

   alpha_r_eq=sqrtf(alpha_r*alpha_r+kk)*sign_alpha_r;

   alpha_t_eq=sqrtf(alpha_t*alpha_t+kk)*sign_alpha_t;

   s=(ssz1+ssz2*(Fy/Fz0_der)+(ssz3+ssz4*dfz)*gamma)*R0*ls;

   Mzr=Dr*cosf(atanf(Br*alpha_r_eq))*cosf(alpha);

   Fy_der=Fy-Svyk;

   // New pneumatic trail

   tmp=Bt*alpha_t_eq;

   t=Dt*cosf(Ct*atanf(tmp-Et*(tmp-atanf(tmp))))*cosf(alpha);



   // Add all aligning forces

   Mz=-t*Fy_der+Mzr+s*Fx;



   // Postprocess; negate for Racer?!

   Fy=-Fy;

   Mz=-Mz;



   // Static results

   latStiffness=-By*Cy*Dy;     // There's that '-' again for lateral force (Fy)

   longStiffness=Bx*Cx*Dx;

}

 

MF6.1实现代码：

rfloat   RPacejka::CalcMz96()

// Calculates aligning moment

{

   rfloat Mz;

   rfloat B,C,D,E,Sh,Sv;

   rfloat FzSquared;

     

   // Calculate derived coefficients

   FzSquared=Fz*Fz;

   C=c0;

   D=c1*FzSquared+c2*Fz;

   E=(c7*FzSquared+c8*Fz+c9)*(1.0f-c10*fabs(camber));

   if((C>-D3_EPSILON&&C<D3_EPSILON)||

      (D>-D3_EPSILON&&D<D3_EPSILON))

   {

     B=99999.0f;

   }   else

   {

     B=((c3*FzSquared+c4*Fz)*(1-c6*fabs(camber))*expf(-c5*Fz))/(C*D);

   }

   Sh=c11*camber+c12*Fz+c13;

   Sv=(c14*FzSquared+c15*Fz)*camber+c16*Fz+c17;

     

   Mz=D*sinf(C*atanf(B*(1.0f-E)*(sideSlip+Sh)+

         E*atanf(B*(sideSlip+Sh))))+Sv;

   return Mz;

}

// Fx - longitudinal

rfloat RPacejka::CalcFx96()

// Pacejka96 model

// Calculates longitudinal force (Fx)

// From G. Genta's book, page 63

// Note that the units are inconsistent:

//   Fz is in kN

//   slipRatio is in percentage (=slipRatio*100=slipPercentage)

//   camber and slipAngle are in degrees

// Resulting forces are better defined:

//   Fx, Fy are in N

//   Mz     is in Nm

{

   rfloat B,C,D,E;

   rfloat Fx;

   rfloat Sh,Sv;

   rfloat uP;

   rfloat FzSquared;

   

   // Calculate derived coefficients

   FzSquared=Fz*Fz;

   C=b0;

   uP=b1*Fz+b2;

   D=uP*Fz;

   

   // Avoid div by 0

   if((C>-D3_EPSILON&&C<D3_EPSILON) || (D>-D3_EPSILON&&D<D3_EPSILON))

   {

     B=99999.0f;

   } else

   {

     B=((b3*FzSquared+b4*Fz)*expf(-b5*Fz))/(C*D);

   }

   

   E=b6*FzSquared+b7*Fz+b8;

   Sh=b9*Fz+b10;

   Sv=b11*Fz+b12;

   

   // Notice that product BCD is the longitudinal tire stiffness

   longStiffness=B*C*D; // *RR_RAD2DEG;    // RR_RAD2DEG == *360/2PI

   

   // Remember the max longitudinal force (where sin(...)==1)

   maxForce.x=D+Sv;

   

   // Calculate result force

   Fx=D*sinf(C*atanf(B*(1.0f-E)*(slipPercentage+Sh)+E*atanf(B*(slipPercentage+Sh))))+Sv;

 

  return Fx;

}

// Fy - lateral

rfloat RPacejka::CalcFy96()

// Pacejka 96

// Calculates lateral force

// Note that B*C*D is the cornering stiffness, and

// Sh and Sv account for ply steer and conicity forces

{

   rfloat B,C,D,E;

   rfloat Fy;

   rfloat Sh,Sv;

   rfloat uP;

   

   // Calculate derived coefficients

   C=a0;

   uP=a1*Fz+a2;

   D=uP*Fz;

   E=a6*Fz+a7;

   

   // Avoid div by 0

   if((C>-D3_EPSILON&&C<D3_EPSILON) || (D>-D3_EPSILON&&D<D3_EPSILON))

   {

     B=99999.0f;

   } else

   {

     if(a4>-D3_EPSILON&&a4<D3_EPSILON)

     {

       B=99999.0f;

     } else

     {

       // Notice that product BCD is the lateral stiffness (=cornering)

       latStiffness=a3*sinf(2*atanf(Fz/a4))*(1.0f-a5*fabs(camber));

       B=latStiffness/(C*D);

     }

   }

   

   Sh=a8*camber+a9*Fz+a10;

   Sv=(a111*Fz+a112)*camber*Fz+a12*Fz+a13;

   

   // Remember maximum lateral force

   maxForce.y=D+Sv;

   

   // Calculate result force

   Fy=D*sinf(C*atanf(B*(1.0f-E)*(sideSlip+Sh)+

   E*atanf(B*(sideSlip+Sh))))+Sv;



   return Fy;

}