1.线段树介绍
线段树是基于区间的统计查询,线段树是一种 二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN),线段树是一颗 平衡二叉树。
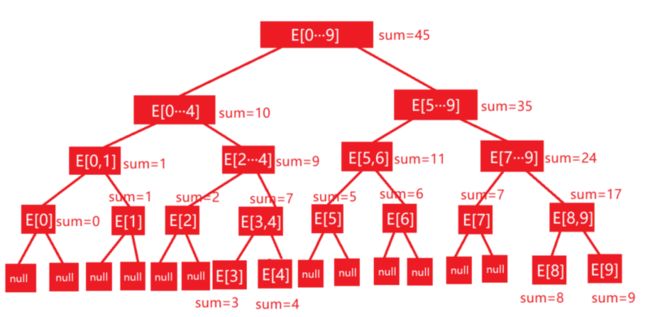
2.线段树示意图
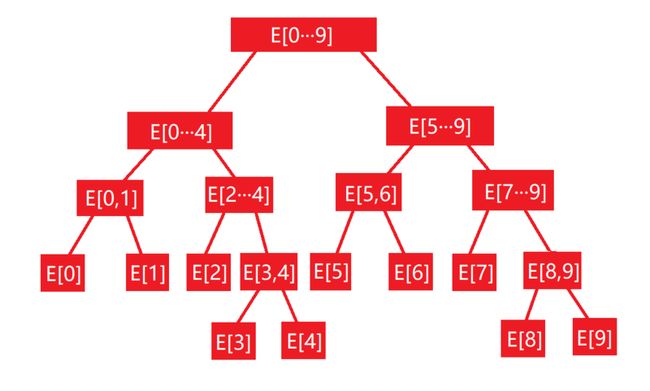
如下图所示,数组 E中,假设区间 0-9 一共 10 个元素,每个儿子节点区间元素的个数都是父亲节点元素个数的一半,若出现 奇数 的情况,则右儿子元素区间比 左儿子 元素区间多一个:
Tips:如图所示的中节点中区间指的是数组
E 的索引值。
3.线段树需要空间分析
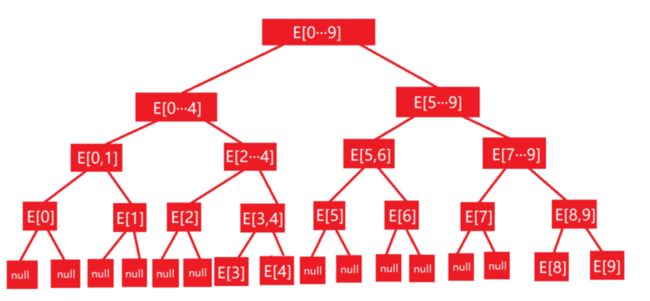
假设我们把 线段树 看做是一颗 满二叉树,并且不考虑添加元素的情况(即区间固定),对于区间有 n 个元素的数组若 n=2^k(k是正整数) 则需要 2n 的空间,最差的情况是若 n=2^k+1 则需要 4n 的空间,如下图所示,最下面一层没有元素的节点使用 null 填充:
Tips: 若索引是从i=0开始的,左儿子left(i) = 2*i+1,右儿子right(i) = 2*i+2,parent(i) = (i-1)/2 取整;
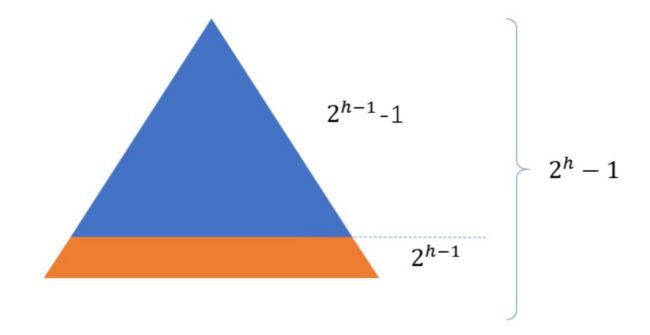
对于满二叉树来说,需要的节点数如下:
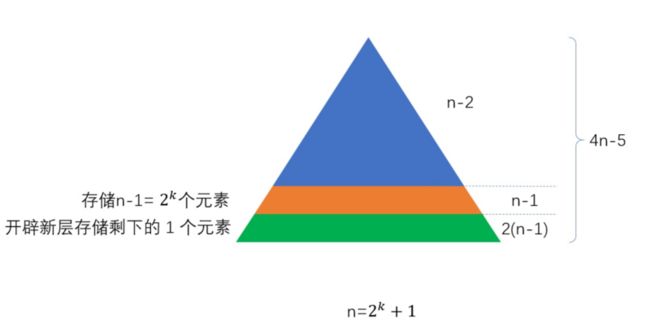
若当 n=2^k+1 需要的的空间数:
Tips:对于区间有n个元素的数组若n=2^k(k是正整数)则需要2n的空间,最差的情况是若n=2^k+1则需要4n的空间就足够了。
4.定义 SegmentTree 线段树类
其中定义了 leftSon($i) 方法,表示求某个节点左儿子节点索引值的方法,rightSon($i) 表示求某个节点右儿子节点 索引值 的方法:
data[$i] = $arr[$i];
}
//若是静态语言需要开 4n 空间来表示 $this->tree
}
public function getSize() {
return count($this->data);
}
public function get(int $index) {
if ($index < 0 || $index >= count($this->data)) {
echo "索引错误";
exit;
}
return $this->data[$index];
}
/**
* 获取某个节点儿子节点索引,若索引是从 i=0 开始的,左儿子 left(i) = 2*i+1
* @param $i
* @return int
*/
private function leftSon($i): int {
return $i * 2 + 1;
}
/**
* 获取某个节点右儿子节点索引,若索引是从 i=0 开始的,右儿子 left(i) = 2*i+2
* @param $i
* @return int
*/
private function rightSon($i): int {
return $i * 2 + 2;
}
}5.创建线段树
接下来使用递归思想去 创建线段树,下面给出递归函数 PHP 代码:
if ($left == $right) {
$this->tree[$i] = $this->data[$left]; //处理递归到叶子节点时 并赋值最原始的 $data 对应的索引值
} else {
$leftSon = $this->leftSon($i); //左儿子索引
$rightSon = $this->rightSon($i); //右儿子索引
$mid = $left + ceil(($right - $left) / 2);//求区间中值
$this->buildSegmentTree($leftSon, $left, $mid - 1); //递归左儿子树
$this->buildSegmentTree($rightSon, $mid, $right); //递归右儿子树
$this->tree[$i] = $this->merge->operate($this->tree[$leftSon], $this->tree[$rightSon]); //这里是根据业务来定节点需要存储的元素
}Tips:其中节点元素存储的值需要根据业务来定,如上面代码表示的是每个节点存储的是区间求和的值,很显然这种方式不灵活,用户在实例化该类的时候可以传入一个merge对象用于元素操作的。
6.节点元素计算规则
上述SegmentTree类中可以在 __construct() 方法中传入一个 $merge 对象,$merge 中可以定义一个 operate() 方法计算得出节点元素值,如下:
merge = $merge;
for ($i = 0; $i < count($arr); $i++) {
$this->data[$i] = $arr[$i];
}
//若是静态语言需要开 4n 空间来表示 $this->tree
//递归创建线段树
$this->buildSegmentTree(0, 0, count($this->data) - 1);
}
private function buildSegmentTree(int $i, int $left, int $right) {
if ($left == $right) {
$this->tree[$i] = $this->data[$left]; //处理递归到叶子节点时 并赋值最原始的 $data 对应的索引值
} else {
$leftSon = $this->leftSon($i); //左儿子索引
$rightSon = $this->rightSon($i); //右儿子索引
$mid = $left + ceil(($right - $left) / 2);//求区间中值
$this->buildSegmentTree($leftSon, $left, $mid - 1); //递归左儿子树
$this->buildSegmentTree($rightSon, $mid, $right); //递归右儿子树
$this->tree[$i] = $this->merge->operate($this->tree[$leftSon], $this->tree[$rightSon]); //这里是根据业务来定节点需要存储的元素
}
}
public function getSize() {
return count($this->data);
}
public function get(int $index) {
if ($index < 0 || $index >= count($this->data)) {
echo "索引错误";
exit;
}
return $this->data[$index];
}
/**
* 获取某个节点儿子节点索引,若索引是从 i=0 开始的,左儿子 left(i) = 2*i+1
* @param $i
* @return int
*/
private function leftSon($i): int {
return $i * 2 + 1;
}
/**
* 获取某个节点右儿子节点索引,若索引是从 i=0 开始的,右儿子 left(i) = 2*i+2
* @param $i
* @return int
*/
private function rightSon($i): int {
return $i * 2 + 2;
}
}6.1 Merge 类定义
如下定义就可以很灵活的处理每个节点的计算规则:
class Merge{
public funcrion operate($left,$right){
//这里可以定义需要操作的规则
return $left+$right; //如求平均值,这里可以 return ($left+$right)/2;
}
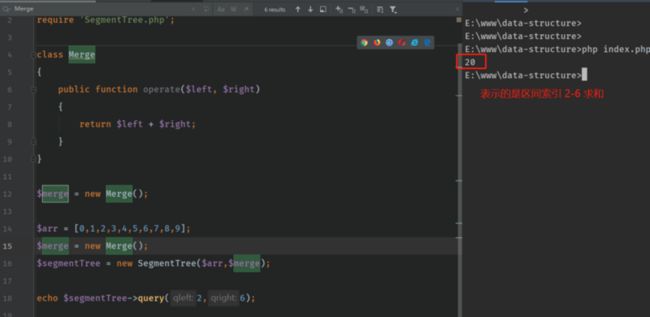
}7. 求和演示
若是各个线段区间存储的是区间求和,则 Merge 类中的 operate() 方法返回是两个元素的和,代码如下:
输出如下:
8. 线段树的区间查询
这里以查询 [2-6] 区间为例,若要查询区间 [2-6] 的求和需要根据区间来寻找需要求的值,示意图如下: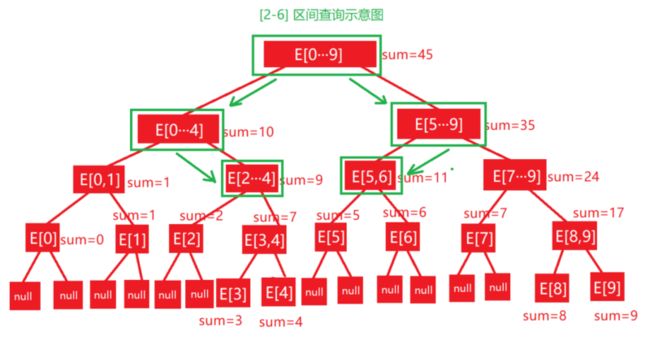
PHP 代码使用递归思想实现如下:
public function query($qleft, $qright) {
if ($qleft < 0 || $qright >= count($this->data) || $qright < $qleft) {
echo "索引范围错误";
exit;
}
return $this->recursionQuery(0, 0, count($this->data) - 1, $qleft, $qright);
}
/**
* 递归查询区间
* @param $left 当前节点区间左端值
* @param $right 当前节点区间右端值
* @param $qleft 需要查询的区间左端值
* @param $qright 需要查询的区间右端值
*/
private function recursionQuery($i, $left, $right, $qleft, $qright) {
$mid = $left + ceil(($right - $left) / 2);//求区间中值向上取整
//先处理满足区间条件的情况
if ($qleft == $left && $qright == $right) { //查询左右端和当前节点左右端重合
return $this->tree[$i];
} elseif ($qright < $mid) { //查询左右端在中值左边,那么结果区间在左儿子树
return $this->recursionQuery($this->leftSon($i), $left, $mid - 1, $qleft, $qright);
} elseif ($qleft >= $mid) { //查询左右端在中值右边,那么结果区间在右儿子树
return $this->recursionQuery($this->rightSon($i), $mid, $right, $qleft, $qright);
} else { //中值在查询左右端中间 将区间分成两边,结果在左右儿子树上都有
$leftSon = $this->recursionQuery($this->leftSon($i), $left, $mid - 1, $qleft, $mid - 1);
$righttSon = $this->recursionQuery($this->rightSon($i), $mid, $right, $mid, $qright);
return $this->merge->operate($leftSon, $righttSon);
}
}9.完整 PHP 代码
9.1 SegmentTree 类
merge = $merge;
for ($i = 0; $i < count($arr); $i++) {
$this->data[$i] = $arr[$i];
}
//若是静态语言需要开 4n 空间来表示 $this->tree
//递归创建线段树
$this->buildSegmentTree(0, 0, count($this->data) - 1);
}
public function query($qleft, $qright) {
if ($qleft < 0 || $qright >= count($this->data) || $qright < $qleft) {
echo "索引范围错误";
exit;
}
return $this->recursionQuery(0, 0, count($this->data) - 1, $qleft, $qright);
}
/**
* 递归查询区间
* @param $left 当前节点区间左端值
* @param $right 当前节点区间右端值
* @param $qleft 需要查询的区间左端值
* @param $qright 需要查询的区间右端值
*/
private function recursionQuery($i, $left, $right, $qleft, $qright) {
$mid = $left + ceil(($right - $left) / 2);//求区间中值向上取整
//先处理满足区间条件的情况
if ($qleft == $left && $qright == $right) { //查询左右端和当前节点左右端重合
return $this->tree[$i];
} elseif ($qright < $mid) { //查询左右端在中值左边,那么结果区间在左儿子树
return $this->recursionQuery($this->leftSon($i), $left, $mid - 1, $qleft, $qright);
} elseif ($qleft >= $mid) { //查询左右端在中值右边,那么结果区间在右儿子树
return $this->recursionQuery($this->rightSon($i), $mid, $right, $qleft, $qright);
} else { //中值在查询左右端中间 将区间分成两边,结果在左右儿子树上都有
$leftSon = $this->recursionQuery($this->leftSon($i), $left, $mid - 1, $qleft, $mid - 1);
$righttSon = $this->recursionQuery($this->rightSon($i), $mid, $right, $mid, $qright);
return $this->merge->operate($leftSon, $righttSon);
}
}
private function buildSegmentTree(int $i, int $left, int $right) {
if ($left == $right) {
$this->tree[$i] = $this->data[$left]; //处理递归到叶子节点时 并赋值最原始的 $data 对应的索引值
} else {
$leftSon = $this->leftSon($i); //左儿子索引
$rightSon = $this->rightSon($i); //右儿子索引
$mid = $left + ceil(($right - $left) / 2);//求区间中值
$this->buildSegmentTree($leftSon, $left, $mid - 1); //递归左儿子树
$this->buildSegmentTree($rightSon, $mid, $right); //递归右儿子树
$this->tree[$i] = $this->merge->operate($this->tree[$leftSon], $this->tree[$rightSon]); //这里是根据业务来定节点需要存储的元素
}
}
public function getSize() {
return count($this->data);
}
public function get(int $index) {
if ($index < 0 || $index >= count($this->data)) {
echo "索引错误";
exit;
}
return $this->data[$index];
}
/**
* 获取某个节点儿子节点索引,若索引是从 i=0 开始的,左儿子 left(i) = 2*i+1
* @param $i
* @return int
*/
private function leftSon($i): int {
return $i * 2 + 1;
}
/**
* 获取某个节点右儿子节点索引,若索引是从 i=0 开始的,右儿子 left(i) = 2*i+2
* @param $i
* @return int
*/
private function rightSon($i): int {
return $i * 2 + 2;
}
}9.2 输出演示代码
query(2,6);代码仓库 :https://gitee.com/love-for-po...
扫码关注爱因诗贤
![]()