什么是“图”
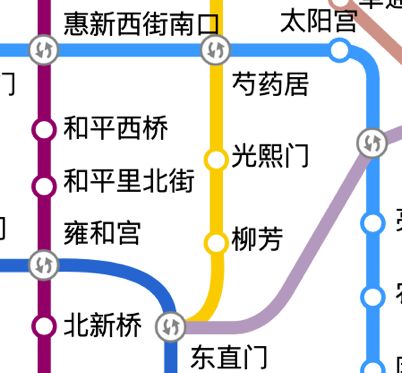
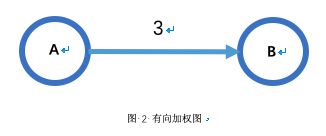
图”由节点和边组成。上面的地铁线路图中从“芍药居”出发到“太阳宫”需要3分种可以用下“图”表示。“图”中描述了“A”和“B”互为邻节点,其中3代表从节点“A”到“B”那条边的权重,边有权重的图称为“加权图”,不带权重的图称为“非加权图”。边上的剪头代表只能从A到B且需要的成本为3,这种边代有方向的图称为“有向图”。
如果“A”能到“B”同时“B”也可以到”A”且成本同样为3则称为“无向图”
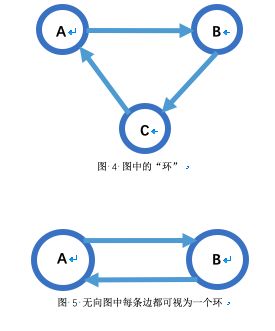
如果存在节“C”使得“A”到 “B”,“B”可以到“C”,“C”又可以到“A”则称“A”、“B”、“C”为一个“环”。 无向图中每一条边最可看为一个环。
狄克斯特拉算法
- 狄克斯特拉算法的试用范围
- 它用于计算加权图中的最短路径
- 只适用于有向无环图,(算法中会屏蔽环路)
- 不能将它用于包含负权边(边的权重为负值)的图
- 算法举例
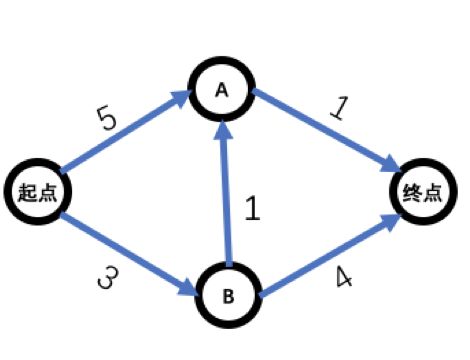
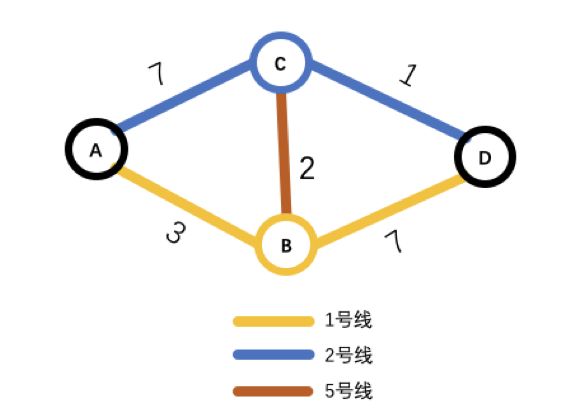
有如下“有向加权图”, 我们要从“起点”出发到“终点”。
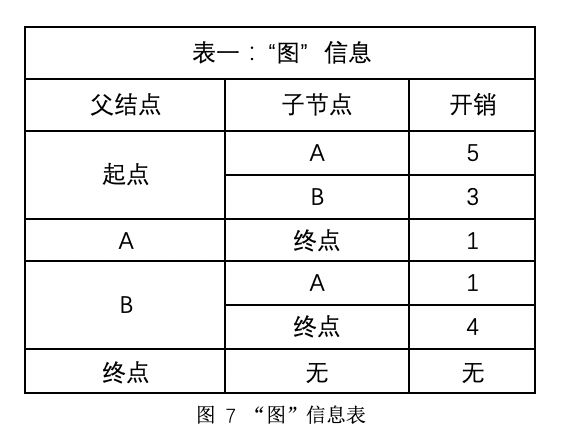
首先需要四个表,用于存储相关信息。
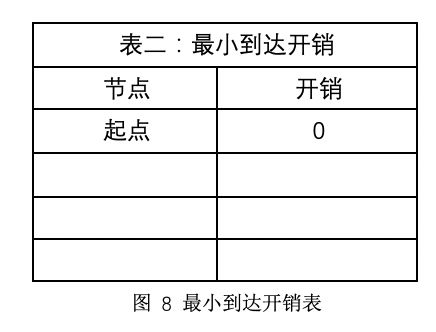
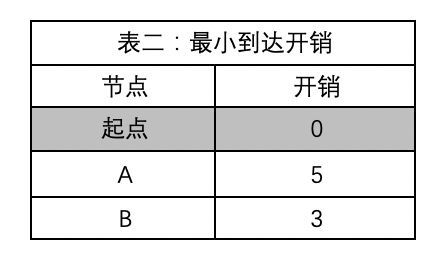
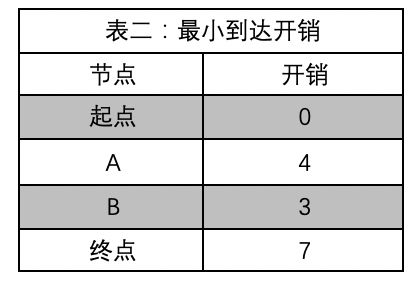
表二: 用于存储每结点从起点出发的最小成本, 开始时只有“起点”成本为0
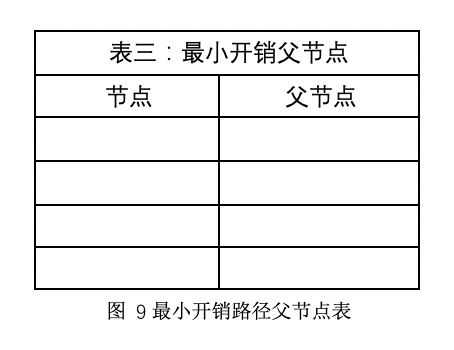
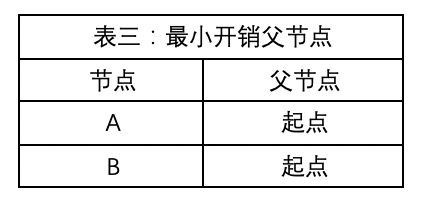
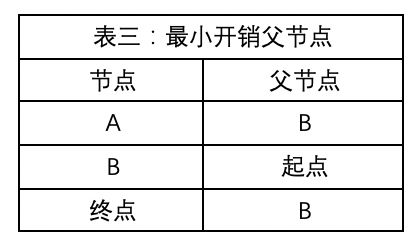
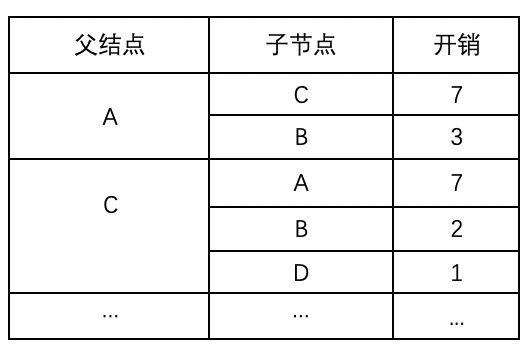
表三:最小开销路径上每结点的父结点
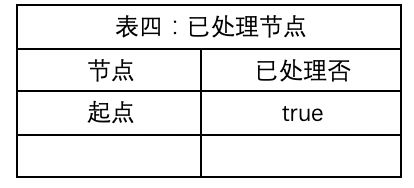
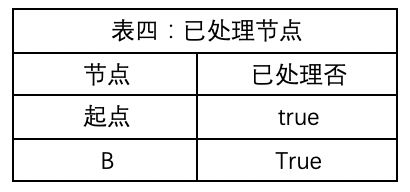
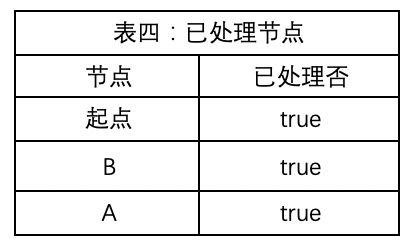
表四:记录结点处理状态
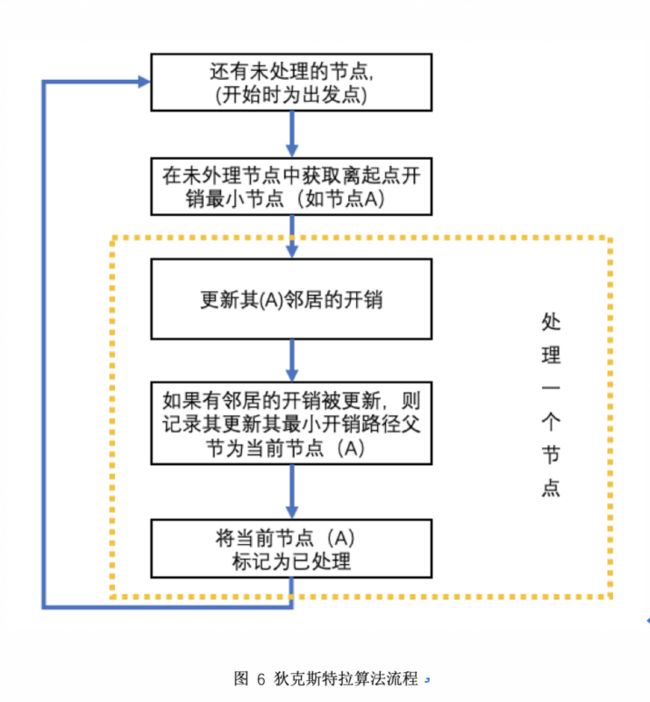
算法流程如下:
1) 从表二及表四中找出最小开销的未处理节点,开始时只有“起点”
2) 从表一中看到从起点出发可以到达A和B开销分别为5和3,更新表二
3) 更新表三记录当前到达A、B点的最小开销父结点为起点
4) 更新表四记录已处理过起点,完成对一个节点的处理
5) (第二轮)从表二及表四中找出未处理过的最小开销的节点“B”(到达成本3)
6) 从表一中看到从B出发可以到达节点A和终点开销分别为1和4
- 由于从B到A的开销1加B的当前的最小到达开销3小于表二中A现有的最小开销5所以更新表二A的最小开销为4并更新表三中A节点的最小到达开销父节点为B。
- 在表二中添加“终点”开销为7 (B到达开销3加B到终点开销4)
- 表三中添加终点父结点为B
7) 记录B点已处理过
8) (第三轮)从表二及表四中找出未处理过的最小开销的节点“A”
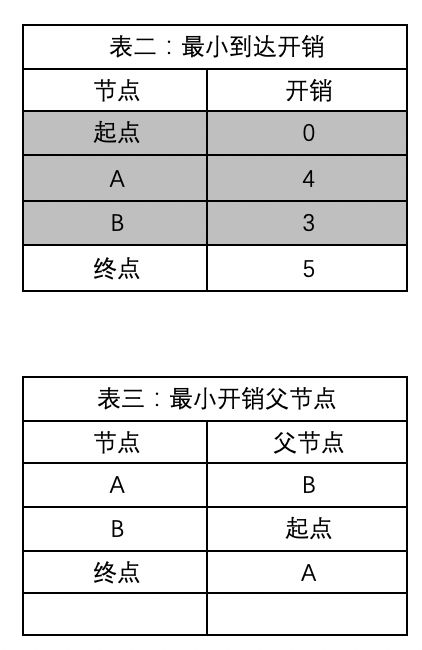
9) 从点A出表可到达终点,点A当前最小到达成本为4 加上A到终点的开销1小于表二中终点当前的最小开销,所以更新表二中终点的开销为5 并更新表三中终点父节点为A
10) 记录A点已处理
11) (第四轮) 从表二及表四中找出未处理过的最小开销的节点:“终点“
12) 由于终点无指向结点无需再处理,支接标记已处理完成终点
13) (第五轮)已无未处理结点完成操作
14) 最终结果
从表二中我们知道终点的最小到达开销为5
从表三中我们可以从终点的父结点一路推出最小开销路径为: 终点 < A < B < 起点
4.代码实现(TypeScript)
/** * 狄克斯特拉查找结果 */
export interface DijkstraFindResult {
/** 差找的图 */
graph: Map>;
/** 开始节点 */
startNode: T_node;
/** 结束节点 */
endNode: T_node;
/** 是否找到 */
isFind: boolean;
/** 最小成本路径节点链*/
parents: Map;
/** 结果路径 */
path: T_node[];
/** 每节点最小到达成本 */
arriveCosts: Map;
}
/**
* 查找未处理过的最小成本节点
* @param costs key:节点信息, value:当前到达成本
* @param processed key:节点信息 value: 是否已处理过
*/
function findMinCostNode( costs: Map, processed: Map): T_node | null {
var minCost: number = Number.MAX_VALUE;
var minCostNode: T_node | null = null;
for (const [node, cost] of costs) {
if (cost < minCost && !processed.get(node)) {
minCost = cost;
minCostNode = node;
}
}
return minCostNode;
}
/**
* 返回从开始节点到结束节点路径
* @param endNode 结束节点
* @param parents key:节点A value:节点A父节点
*/
function getPath( endNode: T_node, parents: Map): T_node[] {
let path = [endNode];
let nParent = parents.get(endNode);
while (nParent) {
path.push(nParent);
nParent = parents.get(nParent);
}
path.reverse();
return path;
}
/**
* 狄克斯特拉查找(找出成本最短路径)
* - 用于加权(无负权边)有向图无环图
* @param graph 要查找的"图", Map<节点 ,Map<相邻节点,到达成本>>
* @param startNode 开始节点
* @param endNode 结束节点
*/
export function dijkstraFind(
graph: Map>,
startNode: T_node,
endNode: T_node): DijkstraFindResult {
/** 到节点最小成本 * k:节点 * v:从出发点到节点最小成本 */
let arriveCosts: Map = new Map();
/** 最小成本路径父节点 k:节点A v: 节点A在最小成本路径上的父节点 */
let parents: Map = new Map();
/** 已处理节点 k: 节点 v: 是否已处理过 */
let processedNode: Map = new Map();
// 设置起点成本为零
arriveCosts.set(startNode, 0);
// 当前节点
let currentNode: T_node | null = startNode;
// 当前节点到达成本
let currentNodeCost: number = 0;
// 当前节点邻节点
let neighbors: Map;
let isFind: boolean = false;
while (currentNode) {
// 标记是否找到目标结点
if (currentNode === endNode) isFind = true;
// 这里costs中一定会有node对映值所以强制转型成number
currentNodeCost = arriveCosts.get(currentNode);
neighbors = graph.get(currentNode) || new Map();
//遍历邻节点更新最小成本
for (const [neighborNode, neighborCost] of neighbors) {
// 邻节点之前算出的最小到达成本
let tmpPrevMinCost = arriveCosts.get(neighborNode);
let prevCost: number = tmpPrevMinCost === undefined ? Number.MAX_VALUE : tmpPrevMinCost;
// 邻节点经过当前节点的成本
let newCost = currentNodeCost + neighborCost;
// 如果经当前结点成本更小,更新成本记录及邻节点最小成本路径父结点
if (newCost < prevCost) {
arriveCosts.set(neighborNode, newCost);
parents.set(neighborNode, currentNode);
}
}
// 记录已处理结点
processedNode.set(currentNode, true);
// 找出下一个未处理的可到达最小成本结点
currentNode = findMinCostNode(arriveCosts, processedNode);
}
// 从起始点到终点路径
let path: T_node[] = [];
if (isFind) {
path = getPath(endNode, parents);
}
return {
isFind: isFind,
path: path,
graph: graph,
arriveCosts: arriveCosts,
parents: parents,
startNode: startNode,
endNode,
};
} //eof dijkstraFind
// 测试
function objToMap(obj: any): Map {
let map: Map = new Map();
for (let k in obj) {
map.set(k, obj[k]);
}
return map;
}
/** 图 */
const graph: Map> = new Map();
graph.set("start", objToMap({ a: 5, b: 3 }));
graph.set("a", objToMap({ end: 1 }));
graph.set("b", objToMap({ a: 1, end: 4 }));
graph.set("end", new Map());
let result = dijkstraFind(graph, "start", "end");
console.log(result);
// 输出
/*
{
isFind: true,
path: [ 'start', 'b', 'a', 'end' ],
graph: Map {
'start' => Map { 'a' => 5, 'b' => 3 },
'a' => Map { 'start' => 5, 'end' => 1, 'b' => 1 },
'b' => Map { 'start' => 3, 'end' => 4, 'a' => 1 },
'end' => Map { 'a' => 1, 'b' => 4 }
},
arriveCosts: Map {
'start' => 0,
'a' => 4,
'b' => 3,
'end' => 5
},
parents: Map {
'a' => 'b',
'b' => 'start',
'end' => 'a'
},
startNode: 'start',
endNode: 'end'
}
*/ 求地铁两站间最小用时路径
把上例中的“图”看成一个地换线路图:现在我们要人A站到D站
将狄克斯特拉算法应用于地铁图对比上面的例子有几个问题.
问题1: 地铁为一个无向图,如A可以到B,B也可以到A ,所以描述图信息时双向的图信息都 要录入,如:
问题2:图中第条边都是一个环,且如A,B,C也可组成一个环是否会对结果产生影响?
不会,因为算法中每次选出的处理节点都是到达成本最小的节点,只有从这个节出发到下一个节点成本更底时才会更新最小成本表和父节点表,且处理过的结点不会再次处理。
问题3: 如何处理换乘线路用时问题?
如:1号线换5号线需要2分种, 5号线换2号线要1分钟。
上图中我们可以看出不考虑换乘从A到D的最少用时路径为:
A > B > C > D
如果算上换乘线路时间最短用时路径为:
A > C > D
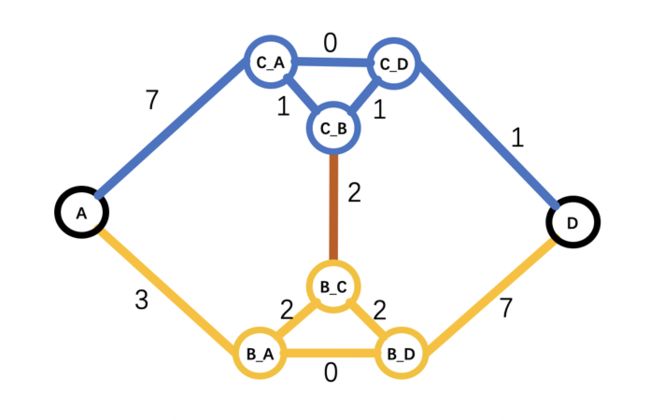
那么如何处理呢?我们可以把换乘站内的换乘路径看成一个局部的图并将其嵌入地铁图中,如:
上图中B结点由 B_A,B_D, B_C 三个结点代替。其中 B_A到B_C,B_D 到B_C 权重相同(也可以不同)代表从1号线换5号线用时2分钟,B_A到B_D权重为0代表从A经由B到D不需要换乘。将上图作为新的算法输入数据就可算出考虑换乘用时的最少用时路径。
参考:
《算法图解》【美】Aditya Dhargava
注:
狄克斯特拉算法部分主要参考算法图解