稳定学习:发掘因果推理和机器学习的共同基础
近年来,因果推理在人工智能研究社区中的热度逐渐提升,许多深度学习领域的顶级科学家也多次指出:因果推理在机器学习中会起到关键性的作用。
因此,近期很多研究方向的工作都或多或少地与因果推理有所结合。在11月27日由「智源社区」举办的 NeurIPS 2020中国预讲会上,来自清华大学计算机科学与技术系的崔鹏副教授发表了主题为「稳定学习:发掘因果推理和机器学习的共同基础」的演讲,崔鹏表示,「我们将站在机器学习的角度,探讨如何看待因果推理。」
本篇文章经 AI 科技评论整理,崔鹏修改并确认。
崔鹏是清华大学长聘副教授,于2010年获得清华大学博士学位,研究兴趣包括大数据环境下的因果推理与稳定预测、网络表征学习,及其在金融科技、智慧医疗及社交网络等场景中的应用。他在数据挖掘和多媒体领域的著名会议和期刊上发表了100多篇论文,并先后获得7项国际会议及期刊最佳论文奖。他于2015年获得ACM中国新星奖,并于2018年获得CCF-IEEE CS青年科学家奖,目前是CCF的杰出会员以及IEEE的高级会员。
作者 | Mr Bear
转载自:AI科技评论
实际上,「因果」的概念在哲学领域已经经历了数百年的发展。上世纪二十年代,「因果」的概念在统计领域出现,也具有相当长的发展历史。至今,「因果」已经成为了一个独立、成熟的研究方向,越来越多机器学习领域的研究者试图通过引入因果的相关概念来解决机器学习中的一些基础问题。
在本次演讲中,崔鹏结合其研究组近年来的相关研究工作,针对如何「将因果与机器学习相结合」这一问题进行了分享。
自 2016 年起,崔鹏的团队开始深入研究如何将因果推理与机器学习相结合,并最终形成了「稳定学习」(stable learning)的研究方向。从宏观的角度来看,稳定学习旨在寻找因果推理与机器学习之间的共同基础,从而应对一系列有待解决的问题。
在演讲中,崔鹏首先介绍了当下人工智能存在的风险,即不可解释性和不稳定性,并指出,关联统计是导致这些风险的重要原因。而结合因果推断的机器学习可以克服这两个缺陷,实现稳定学习。值得一提的是,从因果角度出发,可解释性和稳定性之间存在一定的内在关系,即通过优化模型的稳定性亦可提升其可解释性。
然后,崔鹏介绍了如何通过「混淆变量平衡」的思想实现稳定学习,并指出其具有理论保障。实验结果也表明:「训练和测试时环境差异越大,采用因果方法相对于关联方法取得的性能提升也就越大」,从而展现了因果推断对于降低机器学习风险、克服关联统计缺陷的优势,以及引领机器学习下一个发展方向的潜力。
以下是演讲全文,AI科技评论进行了不改变原意的整理,文章已经过崔鹏修改及确认。
直播地址:https://hub.baai.ac.cn/view/4413
01
研究背景
如今,人工智能技术的应用研究进入了「深水区」,暴露出现有的机器学习方法存在的许多风险和短板。
近年来,互联网为人工智能技术提供了主要的发展「土壤」,催生了许多面向互联网场景的人工智能应用。然而,对于这些技术而言,其技术性风险并不大。
例如,如果搜索引擎或者推荐系统犯了错,并不会招致非常严重的后果。在这样的背景之下,人工智能从业者往往采用了「性能驱动」(performance driven)的方式来优化这些人工智能技术,即我们重点关注该技术在完成目标任务时直观体现出的性能,而并不太关注该技术发生错误时的风险。
然而,在当今人工智能技术应用的大趋势下,越来越多的人工智能应用并不仅仅局限于互联网场景,它们逐渐被用于与人类的生产生活息息相关的一些领域(如医疗健康、法律、交通运输、金融科技),这些领域往往是风险敏感(risk sensitive)的,即人工智能技术产生的错误会招致较大的系统性风险。例如,在医疗健康领域中,此类技术会关系到人的生命安全;而在司法领域,此类技术则关系到社会公平与正义。
因此,我们正面临着人工智能技术从「性能驱动」到「风险敏感」的过渡期,需要更多地关注技术性风险,使人工智能技术可以在高风险的领域中得以广泛而深入的应用。
02
人工智能技术存在的风险
在讨论现有人工智能技术所面临的风险时,我们首先需要关注模型的可解释性问题。如今的深度学习模型大多都是黑盒模型。例如,给定一张医学 CT 影像,我们的算法可以以一定的准确率判断患者患有何种疾病,但是却很难通过某种指标给出人类可以理解的、做出该判断的依据,类似的人类无法理解机器学习系统输出的情况还有很多。
实际上,对于医疗、军事、金融等风险敏感性的应用领域,我们可以预见:「人在回路中」(human-in-the-loop)将是人工智能技术未来被广泛使用的一种模式。
这是因为,对于这些决策存在较高风险的任务而言,当人工智能系统面临的场景十分复杂时,系统很难达到绝对的高精度,并说服人类无条件地信任模型的预测、决策结果。
而要想实现「人在回路中」的模式,首先需要存在人和机器都能够理解的「共同语言」,否则人和机器就无法协作。因此,人工智能技术的可解释性问题严重制约着「人在回路中」的模式,极大地限制了人工智能算法在高风险领域应用的可能性。
此外,统计机器学习等机器学习方法都是建立在数据的独立同分布假设上,我们要求从同一个分布中随机抽样得到训练数据和测试数据,即训练数据和测试数据的概率分布相同。当满足独立同分布假设时,我们可以证明,从理论上说,许多现有的机器学习模型的性能是有所保障的。
然而,在真实场景下,独立同分布假设过于理想,我们实际上并不能保证训练数据和测试数据一定符合某种分布。在开发学习模块的过程中,我们会使用某种训练数据,但是当我们将开发好的模块应用到各种实际场景下时,实际输入数据的分布可能相较于训练数据存在系统性的偏移。
由于现在大多数的机器学习模型都是基于独立同分布假设开发的,当测试数据分布与训练数据分布有系统性偏移时,模型的性能可能降至非常低的水平。举例而言,近年来有许多研究者从事对抗性攻击的研究,当测试数据由对抗性样本组成时,模型的性能甚至可以降至 0。因此,我们需要考虑机器学习模型的稳定性问题,当模型被应用于不同场景下时,我们需要保证模型具有稳定的性能。
示例 1:图像分类
以图像分类为例,尽管当前的模型在我们设计好的理想的环境下取得了很好的性能,但是在更加真实的设定下,该问题还远未得以理想解决。
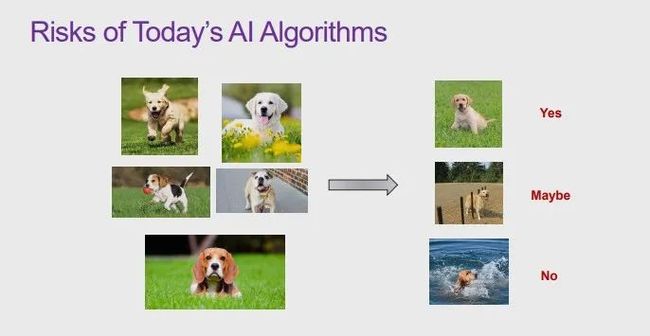
假设我们需要训练一个狗的分类器,此时由包含狗的图片组成的训练数据的分布可能存在一些偏差(bias)。比如在大部分图片中,狗位于草地上,而在另一些数量较少的图片中,狗则处于水泥地上。
在使用符合这种数据分布的训练数据训练好模型后,我们对模型进行测试。如果测试样例为「草地上的狗」时,模型的准确率可能非常高;当测试样例为「沙滩上的狗」时,模型的准确率可能会降至 70% 到 80%;而当测试样例为「水中的狗」时,模型可能会完全失效。
这是因为,「水中的狗」的特征分布相较于训练数据(草地上的狗)是一种非常极端的情况,模型对于这种新的测试样本基本没有判别能力。可见,对于上述简单的图片分类问题,当模型面临现实中比较具有挑战性的环境时,仍然不能被很好地解决。
示例 2:癌症存活率预测
当我们需要基于医疗数据构建一个癌症存活率预测模型(即预测癌症病人可以继续存活的时间)时,也可能存在学习模型不够稳定的问题。
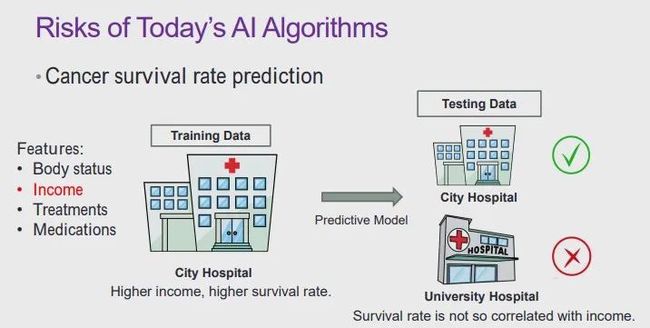
举例而言,假设我们使用的大部分训练数据来自于城市医院等盈利性医院。在对病人建模时,我们会提取其身体状况、治疗方案、收入水平等指标。此时,「收入水平」这项特征的预测能力也许会很强。这可能是因为在盈利性医院中,病人收入水平越高,就可以出更高的价钱买到更好的药,找到更好的医生,得到更好的治疗方案,存活率也就可能高一些。当我们使用从城市医院收集到的数据训练好预测模型后,如果将该模型应用到城市医院的癌症存活率预测任务中,由于训练数据和测试数据概率分布基本一致,所以模型的性能会很高。
然而,如果我们将上述模型应用到大学医学院附属的医院中,就可能会存在非常大的预测性偏差。这是因为,「收入水平」对于在医学院中的癌症存活率预测任务来说,是一个较弱的预测性因子,甚至会对预测起到较大的干扰作用。通常而言,在医学院的医院中,病人用的药和接受的治疗方案可能并不依赖于其支付的费用,而依赖于医学院本身的研究目的。因此,在不同的场景下,这种癌症存活率预测模型的可靠性实际上较差。
03
机器学习模型面临的困境
就当下的人工智能技术而言,由于缺乏可解释性,所以模型的使用者无法理解模型做出预测和决策结果的原因;另一方面,如果模型并不能在各种场景下维持足够稳定的高性能,我们也无法充分信任这些模型。
目前,我们面临着人工智能模型的「可解释性」和「稳定性」都不能得以充分保证的窘境。实际上,如果我们能够保证模型具有足够稳定的高性能,对模型「可解释性」的要求在某种程度上也可以适当降低。
以汽车驾驶为例,并不是所有人都明白汽车的工作原理,但是由于汽车技术在各个层面上都足够可靠,我们仍然可以安心驾驶汽车。
那么,导致当前的人工智能技术面临这种困境的原因是什么呢?在崔鹏看来,当前的大多数机器学习模型都是以「关联统计」为基础的,这也许是造成这种困境的原因之一。
实际上,关联统计手段在某些情况下会存在一些弊端,可靠性无法得以保证。
首先,关联性本身是不可解释的。如图 9 所示,直观地看,红色的曲线与黑色曲线应该高度相关。然而,红色的曲线实际上表示渔船上落水人员的溺死率,而黑色曲线则表示肯塔基州的结婚率。显然,尽管红黑两条曲线相关程度很高,这两份数据其实并没有太大的关系,这种曲线的相关性无法得到解释。
当我们把问题推广到大数据环境下任意的两个趋势性变量时,这两个变量可能并不存在任何物理意义上的关系,但是由于变量 A 和 B 同时为增大趋势或同时为减小趋势,基于关联统计的模型就会认为这两个变量正相关;同理,当 A 和 B 的变化趋势相反时,基于关联的模型则会认为这两个变量负相关。然而,我们无法解释这两种趋势变量的关联性。
因此,对于基于关联统计构造的模型而言,由于我们本身就无法保证关联性的可解释性,所以也就无法从根本上保证模型的可解释性。
另一方面,关联性本身也是不稳定的。如前文所述,关联性的存在与数据分布有很大的关系。如图 10 所示,在训练关于狗的图片分类器时,由于训练数据中包含大量「草地上的狗」,草地和狗的标签之间会形成强相关的关系。当我们在测试时向模型输入「沙滩上的狗」时,图片背景中没有草地,然而模型在训练时会学习到草地和狗之间的强相关性,它会认为背景中没有草地的图片中出现狗的概率也会很小,此时分类模型的置信度也会有所降低。
可见,当我们在测试中切换到与训练数据不同的分布时,关联性是不稳定的。因此,许多研究者将目光投向了「因果性」。
例如,狗的特征空间中,红色的边界框包含一些训练数据中的相关特征,而黄色的边界框中的特征也与狗的标签高度相关。然而,这两种与标签高度相关的边界框中的特征的性质是不同的,黄色边界框中狗的身体上的特征是「因果特征」。对于人类而言,正是因为人类看到了黄色框中的标签才为图片赋予了狗的标签。
当我们依赖「因果特征」进行预测时,即使我们在测试中更换到与训练数据不同的分布,这种因果结构很可能可以保证模型的稳定性,进行更稳定的预测。
04
使用关联性的正确方式
然而,机器学习领域目前暴露出来的问题并不完全是由于「关联性」本身所带来的,它们在更大的程度上是由于我们使用「关联性」的方式造成的。实际上,「关联性」的产生机制有以下三种:
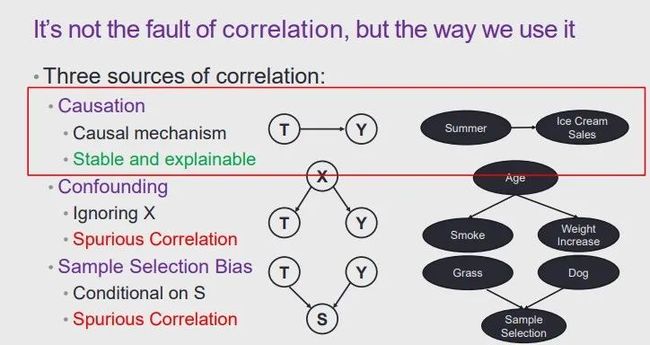
因果:由于 T 导致了 Y,所以 T 和 Y 有所关联(例如,夏天导致冰淇淋销量上升,则夏天与冰淇淋销量之间存在关联),这种因果机制是稳定且可解释的。
混淆:当 X 会导致 T 和 Y 时,T 和 Y 之间就会产生关联(例如,年龄增长可能会导致人倾向于抽烟,而年龄增长可能也会导致人的体重上升,则抽烟和体重上升之间可能会形成关联)。此时 X 的混淆导致 T 和 Y 产生了关联,这种关联实际上是一种虚假的关联,它不可解释也不稳定。
样本选择偏差:如果变量 S 的取值是由T和Y的取值所共同决定,通过控制 S 可以使 T 和 Y 产生关联。在如图 10 所示的例子中,由于存在样本选择偏差(在大多数图片中,狗都在草地上),会使得狗和草地之间会产生关联。从本质上说,这种关联也是虚假关联,是不稳定且不可解释的。
由此可见,在上述三种产生关联的方式中,只有「因果」才是稳定且可解释的,另外两种产生关联的方式都会导致虚假关联。
然而,在我们现在设计机器学习模型的过程中,我们并没有试图区分不同的关联方式。在这种对数据中关联性较为盲目的建模过程中,会产生大量由于「混淆」和「样本选择偏差」导致的虚假关联,从而导致了模型的不可解释和不稳定。因此,我们需要为设计机器学习框架寻找一种新的统计基础。
05
因果与机器学习的结合
实际上,人们很难在定义「因果」的问题上达成共识。从哲学的视角上看,「如何定义因果」、「因果是否存在」都是具有争议的问题。但是从机器学习研究者的角度来说,我们更加关注是否存在一种更好的统计的方式,能够发现数据之间存在的更本质的关联。在此,我们将为「因果」给出一个实用性的定义。
在如图 12 所示的三角形框架中,为了探究 T 是否会导致 Y,我们首先控制住除变量 T 之外所有其它的变量 X。在控制 X 不变的条件下,我们对 T 施加一定的影响,如果 Y 会随着 T 的变化而变化,我们则称 T 对 Y 有因果效应。我们将因果效应的大小定义为:对 T 施加单位扰动时,Y 发生变化的程度。以上就是从干预的角度出发,对因果的一种解释。
将因果的概念引入机器学习领域,会带来一系列好处。在上文中提到的对狗的图像进行分类的例子中,「草」和狗的标签、「狗的鼻子」和狗的标签之间都存在强关联,从关联的层面上说二者区别不大。
然而,从因果的层面上来看,假设 T 代表「草」、Y 代表狗的标签。给定两组数据,在其它特征(例如,狗的鼻子)都相同的情况下,一组数据中有草地,另一组数据中没有草地。我们会发现,这两组数据中狗的标签的百分比分布并没有显著差别。这是因为只要图片中出现了狗的鼻子,无论出现草地与否,都会包含狗。
在这种情况下,我们会发现「草」对标签 Y 实际上并没有因果效应。相对应地,如果令 T 代表「狗的鼻子」,在两组数据中都出现草地的情况下,一组包含狗的鼻子,另一组不包含狗的鼻子,则两组数据中 Y 的百分比分布肯定会存在差异。
因此,通过度量,我们发现「狗的鼻子」对狗的标签有因果效应。在因果的框架下进行度量时,「草」对于狗的标签存在非常弱的因果关系,而「狗的鼻子」和狗的标签存在非常强的因果关系。
可见,如果我们在学习问题中依赖「因果」进行预测,模型的可解释性和稳定性都会得到提升。在此基础之上,崔鹏的团队提出了「稳定学习」的概念。
06
稳定学习
假设我们利用符合分布 1 的训练数据训练机器学习模型,如果我们在测试阶段使用的是同样符合「分布 1」的数据,那么这种情况就是满足独立同分布假设的学习问题。
此外,当我们在测试时使用的是与「分布 1」不同的「分布 n」的数据,我们就需要通过迁移学习技术针对「分布 n」对模型进行优化。
然而,尽管迁移学习技术可以在一定程度上解决这种特征分布偏移的问题,但它所面临的场景仍然不是最普适性的情况。这是因为,在迁移学习框架下,尽管并不要求测试数据和训练数据的分布必须一致,但是我们需要知道测试数据的分布才能进行进一步的域适应。不幸的是,在实际情况下,我们往往无法控制测试数据如何产生。
因此,我们希望在将模型应用到不同的数据分布下的时候,针对准确率的方差进行优化,使准确率的波动可控或者为一个极小的量。同时,另一个需要优化的目标是模型的平均性能。如果我们能够保证模型在不同环境下具有可靠的模型性能,并且能够优化性能波动的方差,那么就可以实现「稳定学习」。
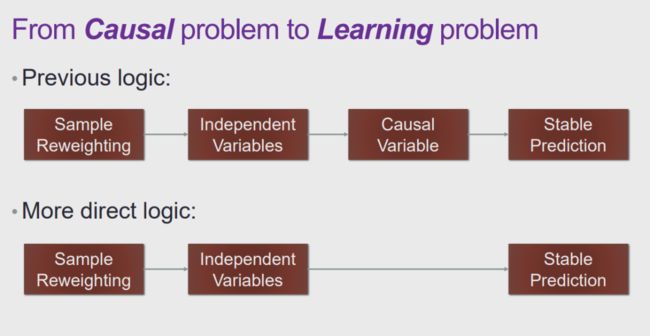
我们将基于因果推理中的「混淆变量平衡」的思想来实现稳定学习。在因果推理领域中,如果我们想要根据可观测的数据估计 T 对 Y 的因果效应,首先要控制其余的所有变量 X 不变。然而实际上,当我们将数据划分为 T=0 和 T=1 的两组后,并不能保证两组数据中变量 X 的分布保持一致。
因此,我们往往会通过使用「直接混淆变量平衡」(directly confounder balancing),即对试验组和对照组两组数据的样本进行加权,使得这两组数据加权后的 X 分布一致,此时这种设定就可以满足上文中对因果效应的定义。实际上,这种操作是通过样本加权的方式使得 T 和 X 相互独立。当 T 和 X 独立之后,度量 T 与 Y 之间的关联性等价于计算 T 与 Y 之间的因果效应。
当我们试图将上述思想推广到机器学习领域中时,一个重要的差异是:在因果领域中,我们度量的是单个变量对输出变量的因果效应,而在机器学习领域中我们需要使用所有的输入变量预测输出变量。
因此,稳定学习旨在将上述思想推广到全局的层面上,试图学习一组样本权重,通过样本加权的方式使所有的输入变量之间都相互独立,从而可以利用现有的基于关联的模型实现基于因果的预测。
07
理论保障
崔鹏在 KDD 2018 上发表的论文「Stable Prediction across Unknown Environments」中,从理论上证明了存在这样的一组权重:即当样本量足够大时,我们可以学习到一组样本权重,使任意的一个干预变量(treatment)都可以与其余所有变量相独立。
在这篇论文中,崔鹏团队的证明是以无限的样本规模为条件的,但在实际应用中,我们无法保证训练样本量无穷大。因此,我们需要在在有限样本的条件下进行一定的优化或近似。
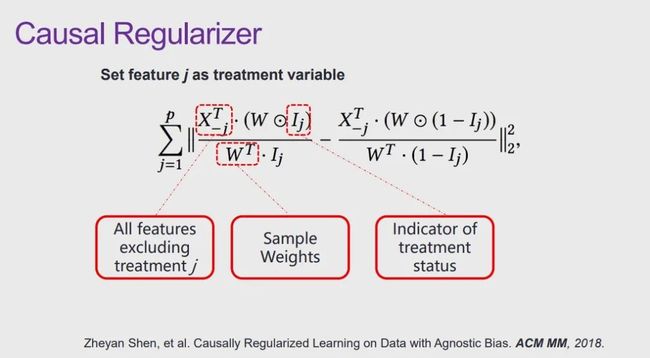
我们引入样本权重W,设计这样一个正则项:对于输入样本的某一维特征,将其作为干预变量T,然后将其余的特征作为需要控制的 X,计算加权后实验组和对照组的样本矩的差的二范数,这一值越小,表明试验组和对照组越平衡;对于输入样本的每一维特征都重复这一过程,将算出的各个二范数加起来,就得到我们所需要的正则项。
在学到样本权重 W 后,我们可以通过一种很自然的方式,在不对现有模型(回归模型、深度学习模型等等)进行较大修改的前提条件下,使用原本基于关联的模型就可以倾向于产生包含因果关系的结果。
具体而言,在上面的优化目标中,我们在 Logistic 的损失中加入了样本权重 W,并额外增加了上面提到的正则项,然后我们迭代优化样本权重W和回归系数β。在最优情况下,干预变量和混淆变量独立,我们估计出的回归系数就暗示了变量 x_i 对输出的因果贡献。
实验验证
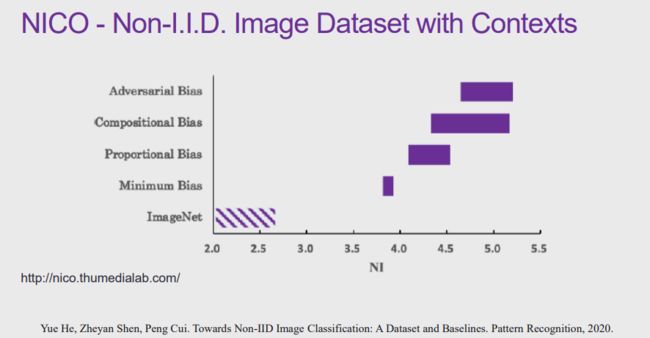
崔鹏团队在各种任务设定下对上述方法进行了验证。在图像分类任务中,团队发布了一个新的数据集「NICO」,它与 ImageNet 最大的区别是:NICO 数据集中的每张图像除了带有类别标注之外,还具有环境标注(例如,在沙滩上、在家中、在草地上等等),每一种环境可能对应数百张图像。
我们希望用包含其中一些环境的数据来训练模型,再用包含其它环境的数据测试模型,即测试模型时使用的环境在训练数据中并不存在,从而评价模型是否能在不同环境下保持稳定的性能。
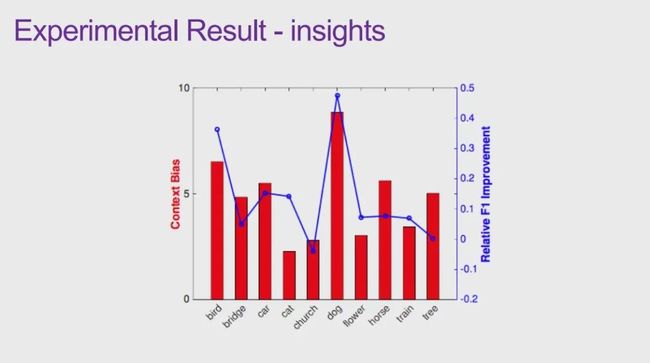
如图 21 所示,红色的竖条为每一类图片的训练数据和测试数据背景环境的差异程度,蓝色折现代表我们通过对样本重新加权将关联模型转换为因果模型后取得的性能提升。可见,训练和测试时环境差异越大,采用因果方法相对于关联方法取得的性能提升也就越大。
同时,通过可视化的方法,我们发现因果模型和基于关联的模型会为不同的特征赋予高权重。如图 22 所示,图中红色的部分是因果模型更为关注的特征,而绿色部分是基于关联的模型更为关注的特征。可见因果模型会自动地赋予目标本身的一些特征以高权重,而基于关联的模型还会赋予一些背景上的特征以高权重。因此,在模型的可解释性层面上,这两种模型的差别较大。
连续变量的稳定学习
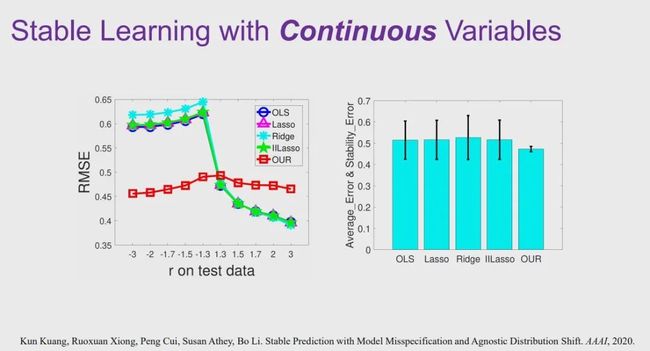
在上文中,我们介绍了对于二值离散变量的稳定学习。在这之后,崔鹏团队又将稳定学习推广到了连续变量的情况下。
如图 24 所示,在连续变量的情况下,采用稳定学习方法后,模型的跨环境的稳定性有很大的提升,误差率在不同环境下的方差有显著的降低。
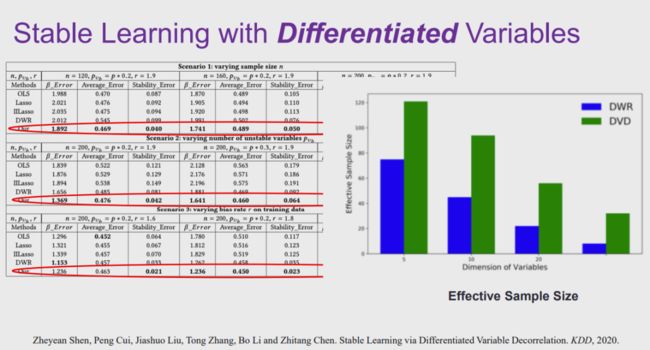
实际上,想要使得所有变量都相互独立是比较困难的目标,这要求我们拥有大量的训练样本。崔鹏团队在 KDD 2020 的论文「Stable Learning via Differentiated Variable Decorrelation」中,针对输入数据中的部分变量,进行使其独立的优化。
08
从因果问题到学习问题
除了从因果的角度对稳定学习进行解释,我们也可以从机器学习的角度出发思考稳定学习问题。
从机器学习的角度来说,模型之所以不稳定是因为它不能够估计出真实的数据产生机制。而估计的模型和真实模型之间的估计误差存在一个上界「2(δ/γ)」,其中 δ 为偏置项的上界,而 γ^2 为输入变量的中心化后的协方差矩阵的最小特征值。γ 描述了输入变量之间的共线性,即它们之间的相关程度。当我们消除掉变量之间的相关性后,γ 就会增大,从而使得估计误差的上界降低。因此,从统计学习的角度来看,我们对输入变量进行独立性的优化,也可以保证模型的稳定性。
09
结语
因果推断与机器学习相结合是一个方兴未艾的研究领域,具有很广阔的探索空间。最近,崔鹏团队为了推动这一领域的研究进展也发布了 NICO 数据集,供有志于从事该领域研究的研究者使用。
当下的人工智能技术往往不能很好地泛化到未知的环境,这是因为这些模型通常只做到了知其「然」(即关联性)而不知其「所以然」(即因果性)。而稳定学习的目标正是在于寻找目前的机器学习方法与因果推理之间的共同基础,从而推进这两个方向的融合。
点击左下角“阅读原文”,观看视频!