复旦大学961-数据结构-第三章-查找（1）-查找的基本概念；对线性关系结构的查找,顺序查找,二分查找

961全部内容链接

查找的基本概念

1. 查找：从一组数据集合中找出符合要求的数据，这个过程称为查找，有两种情况，查找成功和查找失败
2. 查找表：用于查找的数据集合称为查找表，由同一种数据类型组成。可以是数组或链表等数据类型。一般包括四种操作：增删改查。
3. 静态查找表：如果对于一个表，只对该查找表进行查找操作，则称为静态查找表。若对该表进行增删改操作，则该表称为动态查找表
4. 关键字：数据元素中唯一表示该数据的项的值。使用基于关键字的查找，查找结果应该是唯一的（其实可以不唯一，但只能返回一个），如学生表中的学号。
5. 平均查找长度：在查找过程中，一次查找的长度是指在一次查找过程中，要进行关键字比较的次数。平均查找长度(Average search length)是指在所有的查找中关键字比较次数的平均值，公式为：
   $$ASL=\sum _{i=1}^n{P}_i{C}_i$$
   其中，n是查找表的长度，P_i 是第i个元素被查找的概率，一般认为每个元素被查找的概率相等，所以P_i = 1/n 。C_i 是查找第i个元素需要比较的次数。

对线性关系结构的查找

无序表顺序查找

/**
 * 依次遍历，若找到，返回数组下标，若没找到，则返回-1
 */
public static int indexOf(Object[] array, Object x) {
     
    if (array == null) return -1;
    for (int i = 0; i < array.length; i++) {
     
        if (array[i] == x) return i;
    }
    return -1;
}

平均查找长度的计算
$$AS{L}_{成功}=\frac{1+2+\cdots +n}{n}=\frac{1+n}{2}$$
查找不成功时，显然要与所有的元素都对比，所以ASL(失败) = n

有序表的顺序查找

有序表和无序表不一样的地方在于，若比对过程中，如果要查找的元素已经小于当前所在的元素时（假设从小到大），就不用比对后面的了，可以直接返回查找失败。所以对于成功的平均查找长度没有改变，但失败的平均查找长度变小了。

$$\begin{array}{rl}& \\ & AS{L}_{失败}=\frac{1+2+\cdots +n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1}\end{array}$$
公式解释：对于具有n个元素的有序表，共有n+1种查找失败的情况（假设每个查找失败的情况概率相同）。所以分母是n+1。具体参见以下表格进行理解（假设n=4）：

有序表		1		2		3		4
查找失败	(-∞,1)		(1,2)		(2,3)		(3,4)		(4, +∞)
对比次数	1		2		3		4		4

如上述该表格，有序表的元素分别为(1,2,3,4)，所以查找失败的情况有五种，即第二行的五种。每种的对比次数分别是1,2,3,4,4。查找元素区间(3,4)时与4对比，当查找区间(4,+∞)时，也是与4对比，因为4后面没有元素了，所以与4对比完就会直接跳出循环。所以该表的查找失败的平均查找长度为：
$$AS{L}_{失败}=\frac{1+2+3+4+4}{4+1}=\frac{14}{5}$$

Java代码为：

/**
 * 依次遍历，用x与数组中元素比较，若相等，则返回数组下标。若大于，则继续遍历，若小于，直接返回-1
 * 默认该数组是从小到大排序的
 */
public static int indexOf(Comparable[] arrays, Object x) {
     
    if (arrays == null) return -1;
    for (int i = 0; i < arrays.length; i++) {
     
        int result = arrays[i].compareTo(x);
        if (result == 0) return i; // 如果相等，则返回数组下标
        else if (result > 0) return -1; // 如果x
        // 如果x>arrays[i]，则什么都不做，进行下一轮循环
    }
    return -1;
}

二分查找（折半查找）

二分查找仅适用于①顺序存储（数组），②有序表。
基本思想为：先对比数组最中间的元素，若小于该元素（大于时同理）。则递归的对比左边的中间的元素，然后依次递归，直到查找到或查找失败。

其查找成功和查找失败的平均时间复杂度为$$O({\log }_{2}n)$$

判定树

假设有一个有序表(7,10,13,16,19,29,32,33,37,41,43)，将其画成判定树就是如下的形式：

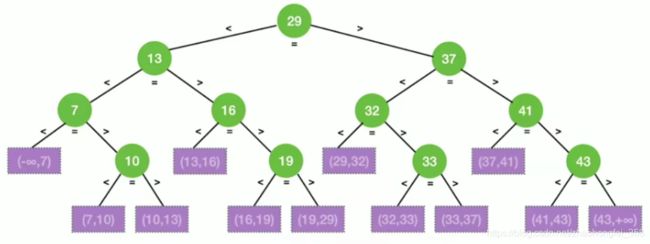
具体画法为：

1. 取中间元素（向下取整）作为根节点，然后其左边的元素和右边的元素分别作为其左子树和右子树
2. 对左子树和右子树分别进行1中的递归操作。直到所有的节点都被画到树中

根据该判定树，可以很容易的推出二分查找成功的平均查找长度，推导过程见如下表格：

层数	该层元素个数	匹配成功该层元素的对比次数
1	2^0=1	1
2	2^1=2	2
3	2^2=4	3
…	…	…
h	2^(h-1)	h

所以，成功的平均查找长度为：
$$AS{L}_{成功}=\frac{1\times 2^0+2\times 2^1+3\times 2^2+\cdots +h\times 2^{h-1}}{n}=\frac{n+1}{n}{\log }_2(n+1)-1\approx {\log }_2(n+1)-1$$
其中n为节点的总数。

二分查找Java代码（非递归）

public static int binarySearch(Comparable[] arrays, Object x) {
     
    if (arrays == null) return -1;
    int left = -1;  // 记录左边界，若这里使用0，则后面都需要相应的改变
    int right = arrays.length; // 记录右边界
    while (left < right - 1) {
      // 当左边界与右边界重合或大于右边界或两个挨着时，查找失败，退出循环
        int mid = (left + right) / 2;
        int result = arrays[mid].compareTo(x);
        if (result == 0) return mid; // 查找成功
        else if (result > 0) right = mid; // x在mid的左边，所以缩短右边界
        else left = mid; // x在mid的右边，所以缩短左边界
    }
    return -1; //查找失败
}

二分查找Java代码（递归）

private static int binarySearch(Comparable[] arrays, Object x, int left, int right) {
     
    if (left > right) return -1;  // 若左边界大于右边界，则说明查找失败
    int mid = (left + right) / 2; 
    int result = arrays[mid].compareTo(x); 
    if (result == 0) return mid;  // 查找成功，返回数组下标
    else if (result > 0) return binarySearch(arrays, x, left, mid - 1); // x在左边，缩小右边界
    else return binarySearch(arrays, x, mid + 1, right); // x在右边，缩小左边界
}

private static int binarySearch(Comparable[] arrays, Object x) {
     
    if (arrays == null) return -1;
    return binarySearch(arrays, x, 0, arrays.length - 1); // 定义边界为 [0,n-1]，n为数组长度
}