复旦大学961-数据结构-第五章-图（一）图的基本概念；图的存储结构,邻接矩阵,邻接表

961全部内容链接

图的基本概念

图的定义

图的定义：图G是由顶点集V和边集E组成，记为G=(V,E)，其中V(G)表示图G中顶点的有限非空集（就是G中的顶点，图不可以是空图）。E(G)表示图G中的顶点之间的关系（边）集合。|V| 表示图G顶点的个数，也称图G的阶，E={(u,v)|u∈V, v∈V}，用 |E| 表示图G中边的条数。图不可以是空图，可以没有边，但不能没有顶点

图的分类

1. 有向图

若图中的边是有向边（也称为弧）时，该图称为有向图。

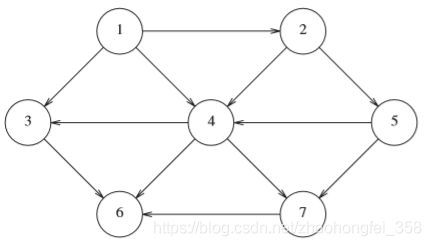
有向边(弧)记为 (v，w是顶点，表示从v->w)，v称为弧尾，w称为弧头，称为从顶点v到顶点w的弧，也称v邻接到w，或w邻接自v。如图所示，使用符号语言表示，则为
$$\begin{gathered} G=(V,E) \\ V=\{1,2,3,4,5,6,7\} \\ E=\{<1,2>,<1,3>,<1,4>,<2,4>,\cdots \} \end{gathered}$$

2.无向图

图中的边没有方向，则图称为无向图，边称为无向边。

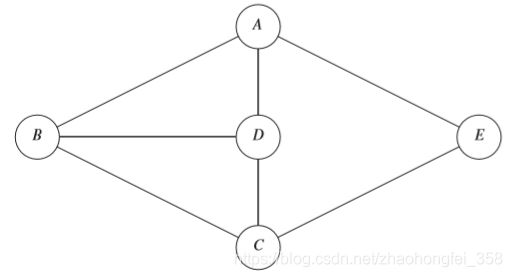
此时，边记为 (v,w)，v，w为顶点，其中 (v,w) = (w,v)。如图所示，用符号语言表示则为：
$$\begin{gathered} G=(V,E) \\ V=\{A,B,C,D,E\} \\ E=\{(A,B),(A,D),(A,E),(B,D),(B,C),(C,E),(D,C)\} \end{gathered}$$

3. 简单图

一个图中，若满足两个条件：

1. 不存在重复边
2. 不存在顶点到自身的边

则该图称为简单图。数据结构中仅讨论简单图

4. 多重图

如果一个图不是简单图，那么它就是多重图。

5. 完全图（也称为简单完全图）

完全图，首先要是一个简单图。第二，能有边的地方一定要有边，那么这个图就成为完全图。完全图又分为无向完全图和有向完全图。无向完全图就是每两个顶点之间一定有一条无向边。而有向完全图是每两个顶点之间一定都有两条方向不同的有向边。

无向完全图边的数量：n(n-1)/2
有向完全图边的数量：n(n-1)

6. 子图

将图G，删除一部分边和一部分顶点得到的图G’，称为图G的子图。类似树中子树的概念。若只删除部分边而不删除顶点，则G’称为G的生成子图。

7. 连通、连通图和连通分量

如果图中的两个顶点之间存在路径，则称两个顶点是连通的。比如 A->B->C，这种的，A和C就是连通的。若图中的任意两个顶点都是连通的，则该图称为连通图。无向图中的极大连通图称为连通分量。

极大连通子图：

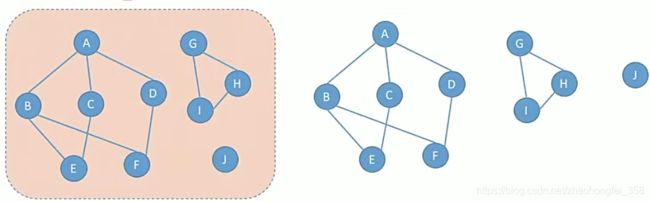
如图所示，橙色部分是一个图。它可以分为三个极大连通子图，即白色区域的。极大连通分量要求子图必须连通，且包含其所有的顶点和边。

极小连通子图：
极小连通子图既要保持连通，又要使得边数最少的子图。

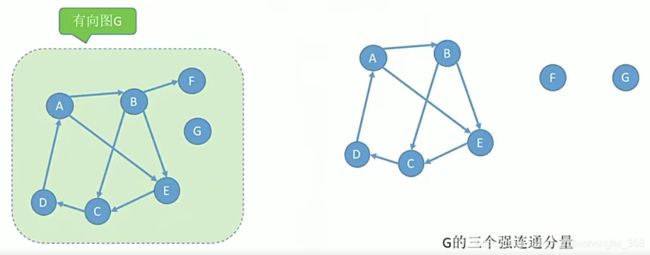
8.强连通图、强连通分量

这两个概念是针对有向图的。如果有向图中，任意两个顶点之间都有路径，则称该图为强连通图。有向图中的极大强连通子图称为有向图的强连通分量。

极大强连通子图：

9. 生成树、生成森林

将一个图砍去一些边，然后把它变成一颗树，那这棵树就称为它的生成树。若一个图存在多个连通分量，把所有的连通分量都给弄成树，组成一个森林。这个森林就称为这个图的生成森林

10. 顶点的度、入度和出度

度的概念类似于树中度的概念。

对于无向图，度是依附于该节点边的数量。

对于有向图，入度就是有多少边指向该节点。出度是指从这个节点出去多少边。

11. 边的权和网

为图的每一条附一个权值，则该图称为带权图，也称为网。

12. 稠密图和稀疏图

边很多的图称为稠密图，边很少的图称为稀疏图。一般认为当 |E| < |V| log|V|时，将G视为稀疏图。

13.路径、路径长度和回路

路径是指一个顶点到另一个顶点都经过了哪些顶点。比如 A->B->C。那么A到C的路径就是A,B,C。其中经过的边的数量称为路径长度。若是第一个顶点和最后一个顶点相同（自身到自身），则该路径称为回路或环。若一个图的顶点数为n, 边数大于 n-1，则该图一定存在回路。

14. 简单路径、简单回路

若一个路径中，不存在重复的路径（顶点），则该路径称为简单路径。若除第一个和最后一个外，不存在重复的路径（顶点）的回路，称为简单回路。

15. 距离

两个节点之间最短的那个路径的长度，称为两个节点之间的距离。若两个节点之间不存在路径，则距离为无穷。

16. 有向树

一个顶点的入度为0，其余节点的入度均为1的有向图，称为有向树。

图的存储结构

图的ADT

public interface Graph<VertexType> {
     

    VertexType[] neighbors(VertexType x); // 返回图中节点x邻近的顶点，,...中的y1,y2

    void insertVertex(VertexType x); // 插入顶点x

    void addEdge(VertexType x, VertexType y); // 插入边  或 (x,y)

    int getVertexNumber(); // 获取顶点的数量

    VertexType getVertexByIndex(int i);  // 根据下标获取节点  
}

图的表示方法

邻接矩阵

使用一个二维数组来表示整个图。arr[n][n] ,其中n为顶点数量。a[i][j] 表示顶点i和顶点j之间是否有边，一般1代表有边，0代表无边。

对于无向图，矩阵是一个对称矩阵。如图：

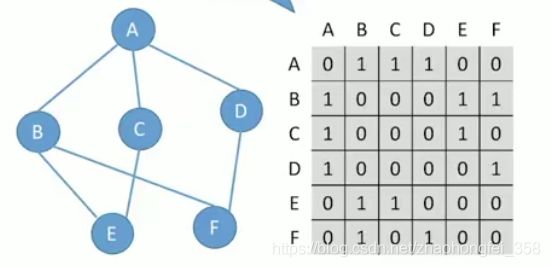
对于有向图，若i->j有边，则arr[i][j] = 1,若j->i，无边，则arr[j][i] =0 ，所以有向图不一定是一个对称矩阵

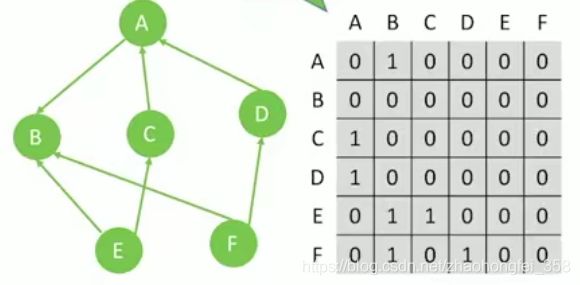
邻接矩阵的特点：

1. 是对称矩阵（无向图）
2. 适合稠密图
3. 可以采用压缩矩阵优化空间
4. 空间复杂度为O(n²)，n为图的节点数|V|

无向图的Java实现

// 邻接矩阵实现无向图
public class AdjacencyMatrixUndirectedGraph<VertexType> implements Graph<VertexType> {
     

    VertexType[] vertexes;  // 节点表
    int[][] edges;  // 边表
    int vertexNumber; // 当前节点数

    public AdjacencyMatrixUndirectedGraph(int maxVertexNum) {
     
        // 初始化
        vertexes = (VertexType[]) new Object[maxVertexNum];
        edges = new int[maxVertexNum][maxVertexNum];
    }

    // 找出顶点x在表中的位置
    private int findIndex(VertexType x) {
     
        for (int i = 0; i < vertexes.length; i++) {
     
            if (x == vertexes[i]) {
     
                return i;
            }
        }
        throw new RuntimeException("图中不包含顶点");
    }

    @Override
    public VertexType[] neighbors(VertexType x) {
     
        ArrayList<VertexType> result = new ArrayList<>();
        int[] edges = this.edges[findIndex(x)];
        for (int i = 0; i < edges.length; i++) {
     
            if (edges[i] == 1) {
     
                result.add(vertexes[i]);
            }
        }
        return (VertexType[]) result.toArray();
    }

    @Override
    public void insertVertex(VertexType x) {
     
        if (vertexNumber >= vertexes.length) {
     
            throw new RuntimeException("容量已满"); // 或进行扩容
        }
        vertexes[vertexNumber] = x; // 将x插入到顶点表的末尾
        vertexNumber++; // 顶点数量+1
    }

    @Override
    public void addEdge(VertexType x, VertexType y) {
     
        int xIndex = findIndex(x);
        int yIndex = findIndex(y);
        edges[xIndex][yIndex] = 1;  // 因为是无向图，所以 (x,y)和(y,x)都要复制为1
        edges[yIndex][xIndex] = 1;
    }

    @Override
    public int getVertexNumber() {
     
        return vertexNumber;
    }

    @Override
    public VertexType getVertexByIndex(int i) {
     
        return vertexes[i];
    }

    public void printGraph() {
     
        System.out.print("\t");
        for (int i = 0; i < vertexNumber; i++) {
     
            System.out.print(vertexes[i] + "\t");
        }
        System.out.println();

        for (int i = 0; i < vertexNumber; i++) {
     
            System.out.print(vertexes[i] + "\t");
            for (int j = 0; j < vertexNumber; j++) {
     
                System.out.print(edges[i][j] + "\t");
            }
            System.out.println();
        }
    }
}

邻接表

如果图是稀疏图，若使用邻接矩阵法，则会有大量的0，显然会很浪费空间。所以引入了邻接表法。邻接表是顺序存储+链式存储实现的，如图所示：

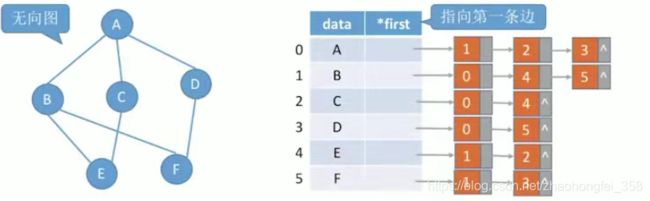
数组中存储的是各个顶点，以及顶点的路径。如图，A顶点有三条路径，分别指向BCD，其下标分别为1,2,3。而1,2,3这三条数据又用一个链表进行存储。1,2,3的顺序没有要求，只是为了表示A节点与BCD节点之间存在边。

若为有向图，原理类似。