复旦大学961-数据结构-第三章-查找（2）-Hash查找法,常见的Hash函数,hash冲突的概念,解决冲突的方法(开散列方法/拉链法,闭散 列方法/开址定址法),二次聚集现现象

961全部内容链接

Hash查找法

Hash表是什么？

Hash表也叫散列表，就是一组数据集合，像List一样，就是存储一组数据，但是它有自己独特的方式。比如在Java中，HashSet与ArrayList一样，都是Collection集合的子类。

Hash表的基本原理

假设现在有一组数据

61，12，46，13，17，28，19，70

如果我们想找里面是否包含28的话，可以将其放入ArrayList中，然后从第一个开始遍历，判断每一项是否与28相等。

那有没有什么方法，不用遍历，瞬间就可以知道这个集合中是否包含28呢。使用Hash表可以解决这个问题。

假设有一个Mod，它的作用是取余

Mod(x) = x % 10

我们初始化一个大小为10数组arr，初始值都为0

0	1	2	3	4	5	6	7	8	9
0	0	0	0	0	0	0	0	0	0

此时，我们对于上面的数字，先进行取余操作，然后根据余数，将其放入对应数组下标中。如：

Mod(61) = 61%10 = 1

所以应该放在61放在arr[1]中。将上述所有数据放入数组中，则如下图所示

0	1	2	3	4	5	6	7	8	9
70	61	12	13	0	0	46	17	28	19

此时，如果要查询28是否在这个集合中，则只需要先对28取余，得到8，然后判断arr[8]是否等于28即可。这样就是就是实现了快速查找。时间复杂度仅为O(1)。

上述描述中，Mod函数被称为 Hash函数，也叫散列函数

假设现在又来了一个数字，为38，取余后，也得8，但是此时arr[8]已经被占用了。那么这种现象就称为冲突。

Hash表要解决的最大的两个问题就是：

1. 如何选择Hash函数，原则是：尽可能等概率，均匀分布，减少冲突
2. 如何解决冲突

常见的Hash函数

1. 直接定址法

直接取关键字作为Hash值，或进行线性变换后的值作为Hash值

H(key) = key  或  H(Key) = a × key + b

这种方法实现简单，不会产生冲突。但是会造成空间的极大浪费。

2. 除留余数法

假定表长为m，取一个不大于m，且接近m的质数p，然后对p求余。

H(key) = key % p

3. 数字分析法

分析要被散列的集合，取相对随机的部分作为散列结果。如，要散列的数据的关键字为身份证号：

412314199607207598
// 6位地区+8位生日+4位随机数

4. 平方取中法

将关键字平方后，取中间几位作为散列地址。具体取多少，视情况而定。这样的好处是，散列地址与关键字每位都有关系，所以分布相对比较均匀。

Hash冲突的概念

散列函数可能会把两个或两个以上的不同关键字映射到同一地址（就是对不同的数据，计算出的hash值一样），这种情况称为Hash冲突，这些发生碰撞的不同关键字称为同义词。

解决冲突的方法

1. 开放定址法

计算hash地址后，发现该地址已经被占用了，那么就找其他的，不属于它的位置，然后放进去。比如：hash函数为对8取余。那 hash(1) =1 和hash(9) = 1，假设先来后到，1先来，那么9就冲突了，那么9就可以放在其他位置，比如放在2位置。

对于放在哪个位置，又可以有下面几种方法：

1.1 线性探测法

就是依次往后探测，直到找到一个可以存放的位置。比如，hash(9)=1, 但是1位置已经被占了，那就看看2有没有，如果2也被占了，那就看3，依次类推。

缺点是会出现大量元素在相邻的散列地址上“聚集”，这种现象称为二次聚集现象。造成查找效率低下

1.2 平方探测法

探测的顺序为

$$0^2,1^2,-1^2,2^2,-2^2，\cdots$$

假设数组长度为20，目前10位置冲突了，那么往后找的时候，分别找 11,9,14,6，依次类推。

优点为可以避免堆积，缺点为不能探测Hash表上的所有位置

1.3 再散列法

用另一个Hash函数求出探测时的增量

1.4 伪随机法

增量使用随机数

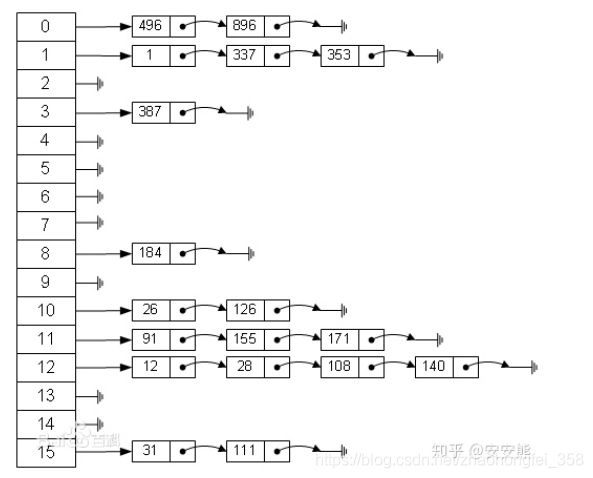
2.拉链法

如果Hash地址一样，那么就依次往后排，按先来后到的方式。就像这个样子。可以使用数组，也可以使用链表。

二次聚集现象

在上面 开放定址法 的 线性探测法 有提到