机器学习入门实战---波士顿房价预测
波士顿房价预测
波士顿房价数据集介绍
波士顿房价数据说明:此数据源于美国某经济学杂志上,分析研究波士顿房价( Boston HousePrice)的数据集。数据集中的每一行数据都是对波士顿周边或城镇房价的情况描述。本问题是一个回归问题。每个类的观察值数量是均等的,共有 506 个观察,13 个输入变量和1个输出变量。
数据特征:
- CRIM: 城镇人均犯罪率
- ZN: 住宅用地所占比例
- INDUS: 城镇中非住宅用地所占比例
- CHAS: 虚拟变量,用于回归分析
- NOX: 环保指数
- RM: 每栋住宅的房间数
- AGE: 1940 年以前建成的自住单位的比例
- DIS: 距离 5 个波士顿的就业中心的加权距离
- RAD: 距离高速公路的便利指数
- TAX: 每一万美元的不动产税率
- PTRATIO: 城镇中的教师学生比例
- B: 城镇中的黑人比例
- LSTAT: 地区中有多少房东属于低收入人群
- MEDV: 自住房屋房价中位数(也就是均价)
一、加载需要的包
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import numpy as np
二、数据预处理
(1)读入数据和观察数据 看看是否需要进行数据预处理。如是否需要 1. 去除唯一属性;2. 处理缺失值;3. 特征编码;4. 数据标准化、正则化; 5. 特征选择(降维)
dataset = load_boston()
x_data = dataset.data
y_data = dataset.target
name_data =dataset.feature_names
print(name_data)
输出结果:
[‘CRIM’ ‘ZN’ ‘INDUS’ ‘CHAS’ ‘NOX’ ‘RM’ ‘AGE’ ‘DIS’ ‘RAD’ ‘TAX’ ‘PTRATIO’
‘B’ ‘LSTAT’]
(2)特征工程-可视化各个特征与房价的关系
for i in range(13):
plt.subplot(7,2,i+1) #7行2列第i+1个图
plt.scatter(x_data[:,i],y_data,s=10) #横纵坐标和点的大小
plt.title(name_data[i])
plt.show()
print(name_data[i],np.corrcoef(x_data[:i]),y_data)
#打印刻画每个维度特征与房价相关性的协方差矩阵
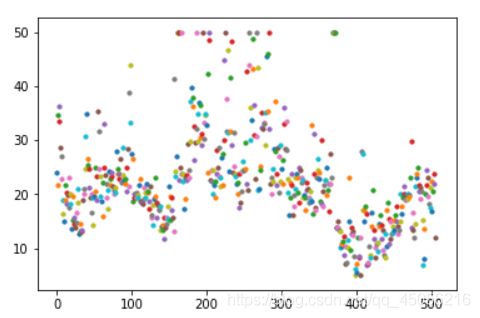
查看房价数据分布,发现有一部分数据等于50,视为异常数据
for i in range(len(y_data)):
plt.scatter(i,y_data[i],s=10) #横纵坐标和点的大小
(3)、特征工程-处理数据 基于散点图,分析因变量与自变量的相关性,把不相关的数据剔除。经过上面散点图的分析,可以看到数据异常的变量需要特殊处理,根据散点图分析,房屋的’RM(每栋住宅的房间数)’,‘LSTAT(地区中有多少房东属于低收入人群)’,'PTRATIO(城镇中的教师学生比例)’特征与房价的相关性最大,所以,将其余不相关特征剔除。
i_=[]
for i in range(len(y_data)):
if y_data[i] == 50:
i_.append(i)#存储房价等于50 的异常值下标
x_data = np.delete(x_data,i_,axis=0) #删除样本异常值数据
y_data = np.delete(y_data,i_,axis=0) #删除标签异常值
name_data = dataset.feature_names
j_=[]
for i in range(13):
if name_data[i] =='RW'or name_data[i] == 'PTRATIO'or name_data[i] == 'LSTAT' : #提取'RM'、'PTRATIO'、'LSTAT'三个主要特征
continue
j_.append(i)#存储其他次要特征下标
x_data = np.delete(x_data,j_,axis=1)#在总特征中删除次要特征
print(np.shape(y_data))
print(np.shape(x_data))
for i in range(len(y_data)):
plt.scatter(i,y_data[i],s=10)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test =train_test_split(x_data,y_data,random_state = 0,test_size = 0.20)
print(len(X_train))
print(len(X_test))
print(len(y_train))
print(len(y_test))
输出结果:
392
98
392
98
(5)、数据归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
X_train = min_max_scaler.fit_transform(X_train)
X_test = min_max_scaler.fit_transform(X_test)
#标签归一化的目的是什么呢,实验证明,归一化之后结果好了0.1左右
y_train = min_max_scaler.fit_transform(y_train.reshape(-1,1)) #转化为任意行一列
y_test = min_max_scaler.fit_transform(y_test.reshape(-1,1)) #转化为一列
三、模型训练
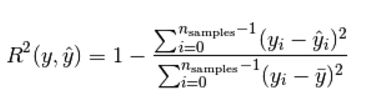
越接近1效果越好,为0表示与取均值接近,为负则表示连平均值都不如
1.线性回归
from sklearn import linear_model
#请完成线性回归的代码,生成lr_y_predict作为测试集的预测结果
lr = linear_model.LinearRegression() #选择线性回归模型
lr.fit(X_train,y_train) #模型的训练
lr_y_predict = lr.predict(X_test) #预测数据
from sklearn.metrics import r2_score
score_lr = r2_score(y_test,lr_y_predict)
score_lr
其中lr_y_predict为预测出的结果,score_lr表示的为使用测试数据查看该模型训练是否较好
结果:0.6439270371515048
2.岭回归
#请完成岭回归的代码,并设置适当的alpha参数值
rr=linear_model.Ridge() #选择模型岭回归
rr.fit(X_train,y_train) #模型的训练
rr_y_predict=rr.predict(X_test)
score_rr = r2_score(y_test,rr_y_predict)
score_rr
结果:0.6393923188987708
3.lasso
lassr = linear_model.Lasso(alpha=.0001)
lassr.fit(X_train,y_train)
lassr_y_predict=lassr.predict(X_test)
score_lassr = r2_score(y_test,lassr_y_predict)
print(score_lassr)
4.SVR
from sklearn.svm import SVR
svr_rbf = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=.1) #高斯核
svr_lin = SVR(kernel='linear', C=100, gamma='auto') #线性核
svr_poly = SVR(kernel='poly', C=100, gamma='auto', degree=3, epsilon=.1,
coef0=1) #径向基核函数
svr_rbf_y_predict=svr_rbf.fit(X_train, y_train).predict(X_test)
score_svr_rbf = r2_score(y_test,svr_rbf_y_predict)
svr_lin_y_predict=svr_lin.fit(X_train, y_train).predict(X_test)
score_svr_lin = r2_score(y_test,svr_lin_y_predict)
svr_poly_y_predict=svr_poly.fit(X_train, y_train).predict(X_test)
score_svr_poly = r2_score(y_test,svr_poly_y_predict)
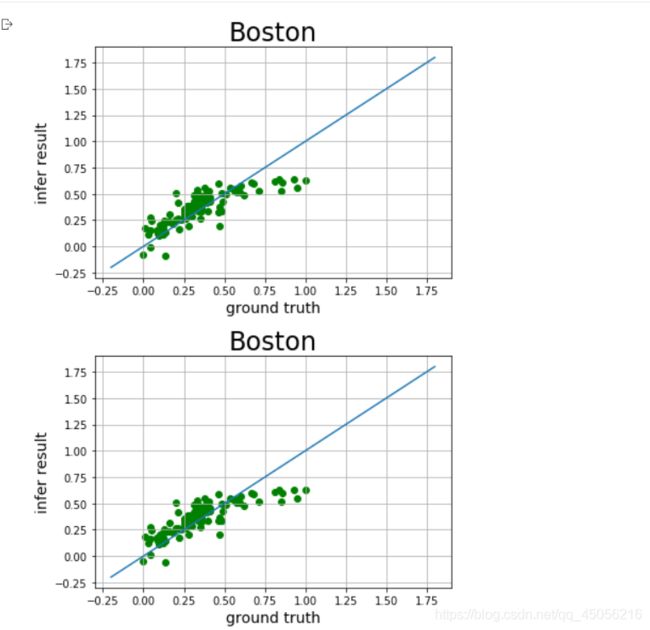
#绘制真实值和预测值对比图
def draw_infer_result(groud_truths,infer_results):
title='Boston'
plt.title(title, fontsize=24)
x = np.arange(-0.2,2)
y = x
plt.plot(x, y)
plt.xlabel('ground truth', fontsize=14)
plt.ylabel('infer result', fontsize=14)
plt.scatter(groud_truths, infer_results,color='green',label='training cost')
plt.grid()
plt.show()
draw_infer_result(y_test,lr_y_predict)
draw_infer_result(y_test,rr_y_predict)
draw_infer_result(y_test,lassr_y_predict)
draw_infer_result(y_test,svr_rbf_y_predict)
draw_infer_result(y_test,svr_lin_y_predict)
draw_infer_result(y_test,svr_poly_y_predict)
print("score of lr:",score_lr)
print("score of rr:",score_rr)
print("score of lassr:",score_lassr)
print("score of svr_rbf:",score_svr_rbf)
print("score of svr_lin:",score_svr_lin)
print("score of svr_poly:",score_svr_poly)