Kmeans 算法理论和Python实现(一)——简单K-Means实现
#1. Kmeans算法原理
##1.1 Kmeans算法介绍
聚类算法是一种无监督学习方法,将相似的对象归到同一个簇中。在K-Means算法中,我们将所有的数据划分到K个不同的簇中并且每一个簇的中心是该簇中所有的节点的均值计算得到,因此称为K—均值算法。
在机器学习中聚类和分类算法最大的不同在于,分类的目标事先是已知的,而聚类则不同,聚类的目标是未知的。分类产生的结果是分类前已经知晓的结果,而聚类产生的结果是未知的,因此聚类别称为无监督的学习方式。
##1.2 Kmeans算法原理
K-Means算法是发现给定数据集中的K个簇而簇的个数K是用户给定的数据信息,每一个簇通过簇的质心来描述,质心是通过该类中的所有点求平均值得到。
在K-Means算法中,算法的流程如下:
(1)随机选择K个点作为初始质心
(2)对所有的点计算寻找最近的质心为该点所属的质心,并计算到该质心的距离。
(3)对各个节点划分好的点通过求该簇所有节点的均值计算该簇新的质心。
(4)重复步骤(2)对所有的节点重新进行划分,直到所有的簇的质心不再改变。
在计算节点与质心之间的距离时,我们通常采用欧式距离进行计算计算公式如下:
d i s t = s q r t ( ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + . . . + ( x i − y i ) 2 ) dist=sqrt((x_1-y_1)^2+(x_2-y_2)^2+...+(x_i-y_i)^2) dist=sqrt((x1−y1)2+(x2−y2)2+...+(xi−yi)2)
根据上述描述的过程Kmeans算法执行的过程主要为:计算质心——划分节点——重新计算的过程,接下来我们考虑如何实现K-Means算法
#2. Kmeans算法Python实现
##2.1 初始化质心
def Random_initCentroids(dataSet, k):
numSamples, dim = dataSet.shape
centroids = zeros((k, dim))
#随机生成聚类中心
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataSet[index, :]
return centroids
在上述代码中,在所有的数据节点中随机选择一个节点作为聚类中心,在Random_initCentroids()中通过随机的选择所有的点中的任意K个作为聚类中心。其中Random_initCentroids()传入的参数分别为:
dataSet和k值,在随机选择时同样同样的可以在每一个特征的最小值和最大值之间随机选取一个值作为初始的质心。
##2.2 计算节点距离
def euclDistance(vector1, vector2):
return sqrt(sum(power(vector2 - vector1, 2)))
上述代码用于计算两个向量之间的距离,也就是节点vector1和节点vector2之间的距离在这里的距离表示的欧式距离。
##2.3 Kmeans聚类
def kmeans(dataSet, k,medthod):
numSamples = dataSet.shape[0]
# first column stores which cluster this sample belongs to,
# second column stores the error between this sample and its centroid
clusterAssment = mat(zeros((numSamples, 2)))
clusterChanged = True
## 初始化聚类中心
if medthod == 0:
centroids = Random_initCentroids(dataSet, k)
else:
centroids = maxDis_initCentroids(dataSet, k)
while clusterChanged:
clusterChanged = False
## 对每一个点计算聚类中心
for i in range(numSamples):
minDist = 100000.0
minIndex = 0
## 寻找最近的聚类中心
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
##更新节点所属的簇判断迭代是否继续
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist ** 2
## 更新聚类中心
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis=0)
print('Congratulations, cluster complete!')
return centroids, clusterAssment
在上述的Kmeans聚类算法中主要的执行过程如下:
(1)初始化聚类中心
根据下面的代码可知,在我们这里定义了两种初始化聚类中心的方式一种为上面讲述的Random_initCentroids()随机选取聚类中心的方式,另外一种为maxDis_initCentroids()方式,第二种聚类方式我们在下面做详细的介绍。
clusterAssment = mat(zeros((numSamples, 2)))
clusterChanged = True
## 初始化聚类中心
if medthod == 0:
centroids = Random_initCentroids(dataSet, k)
else:
centroids = maxDis_initCentroids(dataSet, k)
(2)计算每一个结点所有的簇
对数据集中的所有节点计算出距离最小的质心,并将该节点划分到质心所属的簇。
while clusterChanged:
clusterChanged = False
## 对每一个点计算聚类中心
for i in range(numSamples):
minDist = 100000.0
minIndex = 0
## 寻找最近的聚类中心
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
##更新节点所属的簇判断迭代是否继续
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist ** 2
(3)更新质心
对统计簇中每一个点的每一维特征的均值作为新的质心,并重复上述步骤(2)直到所有簇的质心都不再发生改变为止。
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis=0)
##2.4 数据可视化
在Python中我们可以通过matplotlib对二维的数据进行可视化。
def showCluster(dataSet, k, centroids, clusterAssment):
numSamples, dim = dataSet.shape
printCluster(dataSet, centroids, clusterAssment)
if dim != 2:
print("Sorry! I can not draw because the dimension of your data is not 2!")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark):
print
"Sorry! Your k is too large! please contact Zouxy"
return 1
# draw all samples
for i in range(numSamples):
markIndex = int(clusterAssment[i, 0])
plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ' ##2.5 数据输出
输出整个数据集的所有簇的质心以及每一个每一个数据项对应的簇和该簇的质心。
def printCluster(dataSet, centroids, clusterAssment):
numSample,dim = dataSet.shape
i = 0;
for a in centroids:
print("Cluster ",i,"centroids is ",a);
i = i + 1
for i in range(numSample):
print("the node ",dataSet[i]," belong to the cluster",clusterAssment[i],"the centroids is ",centroids[int(clusterAssment[i,0])]);
##2.6 测试代码
from numpy import *
import time
import matplotlib.pyplot as plt
## step 1: load data
from src.Kmeans import kmeans, showCluster
print("step 1: load data...")
dataSet = []
fileIn = open('../data/Iris.txt')
#read each line in the file
for line in fileIn.readlines():
linedata = []
lineArr = line.strip().split(',')
for data in lineArr:
linedata.append(float(data));
dataSet.append(linedata)
print("step 2: clustering...")
dataSet = mat(dataSet)
k = 3
centroids, clusterAssment = kmeans(dataSet,k,1)
## step 3: show the result
print("step 3: show the result...")
showCluster(dataSet, k, centroids, clusterAssment)
#3. 运行结果
在测试算法的聚类效果时,我们分别选取了两个数据集进行聚类,一个是在参考的博客中给出的数据集,是一个二维的数据集,一个失鸢尾花数据集。
##3.1 二维数据集
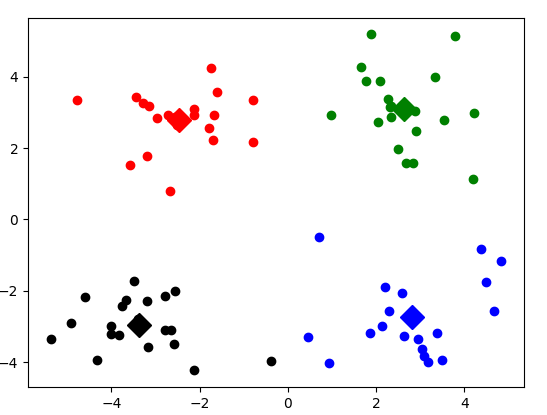
下面如下图1为matplotlib绘制出的二维图像,我们将所有的数据一共聚成4个类,根据下述图中的显示的结果可知,Kmean算法具有较好的聚类效果。
对于聚类后的输出数据如下图2所示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hgCTyw9f-1595748821806)(Image/2.png)]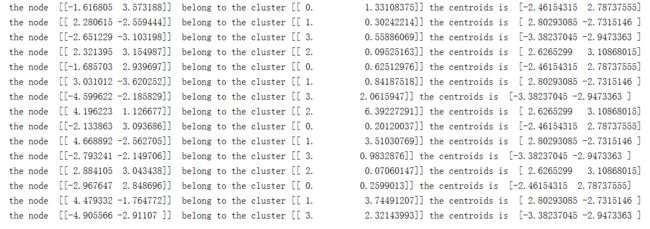
##3.2鸢尾花数据集
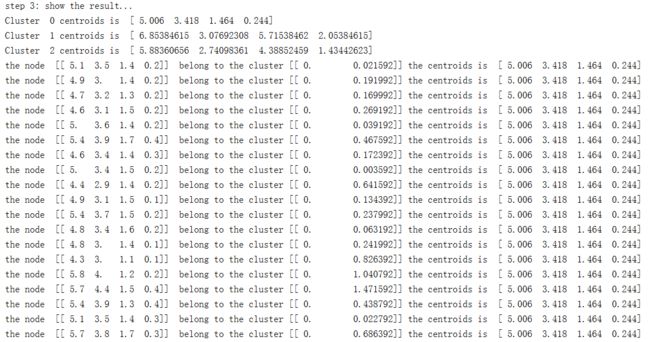
对于鸢尾花数据集聚类的结果输出如下所示,我们将数据结果一共聚类成3个类。
#4. Kmeans算法的优缺点及改进方法
##4.1 Kmens算法的优点
(1)实现简单,易于理解
##4.2 Kmeans算法的缺点
(1)可能收敛到局部最小值,在大规模数据集上收敛较慢
(2)只适用于数值型的数据
(3)对初始质心的比较敏感。
(4)无法聚类非球状数据
(5)在较大数据集上收敛速度慢
##4.3 Kmeans聚类性能提高
为了解决聚类算法对处置敏感性的问题,防止Kmeans算法收敛到最小值的可能收敛到局部的最小值,我们通过改变质心的初始化方式来解决这一问题,根据上述描述的方式,我们在初始化聚类中心时采用随机初始化聚类中心的方式。为了减小聚类中心对初始值的敏感性,我们对聚类中心的初始化方式有以下两种:
(1)通过最大距离的方式初始化聚类中心。
根据下述的代码可知,通过maxDistance初始化聚类中心时,第一个质心通过随机选取,在此之后所有质心的选择都选择与当前已经选择作为质心的点最远的点作为新的质心。
def maxDistance(dataSet,centroids,numCentroids):
numSamples,dim = dataSet.shape;
maxDis = 0;
maxindex = 0;
for i in range(numSamples):
distance = 0;
for j in range(numCentroids):
distance = euclDistance(dataSet[i,:],centroids[j,:]) + distance;
if distance > maxDis:
maxDis = distance;
maxindex = i;
centroids[numCentroids,:] = dataSet[maxindex,:]
(2)通过分层聚类初始化聚类中心
通过Canopy进行分层聚类,在每一个Canopy中选择一个点作为质心进行聚类,得到最终的聚类结果。
此外还有一些聚类的后处理方式以及二分K-均值聚类算法在之后进行描述
博客源代码下载地址