kmeans结合Canopy算法的python实现

一. 实验目的及原理

通过分析K-Means聚类算法的聚类原理，利用高级编程语言实现K-Means聚类算法，并通过对样本数据的聚类过程，加深对该聚类算法的理解与应用过程

二. 数据的准备及预处理

实验所用编程语言：python
开发环境：PyCharm
实验所用数据集：随机生成的100组横纵坐标取值范围在（0，100）的坐标点

三．算法设计

设计算法前的思考：

k-means算法本身的逻辑和实现并不复杂，计算的复杂度较低，并且保持有较好的伸缩性，因此不仅适用于小数据集，也同样适用于大数据背景下的数据聚类分析。但其的缺点也很明显，算法本身的性能十分依赖与初始值K的确定以及初始中心点的设立，以及对噪声敏感。为了解决k-means算法的这些问题，引进Canopy算法，为k-means算法先粗略生成K个中心点，k-means算法使用这K个中心点将大大减少其本身的迭代次数。

对于Canopy算法，其本质上是根据T1、T2两个参数确定簇和簇的中心点，大于T1会被认为是离本簇中心点过远因而去除，小于T2会被认为离本簇的中心点过近，因此不适宜做另一个簇的中心点。通过这两点逻辑对数据集的每一个点进行筛选，首先会排除掉过于偏离的噪声点，同时，也会生成一定数量的相对距离较为合理的中心点。但是，Canopy算法的缺点也很明显，就是其两个参数T1和T2的确立问题，关于这一点我在网上也没有找到相关的较为科学高效方法。
以下是Canopy算法的具体实现步骤：

1. 对原数据集进行一定规则的排序，这个排序是任意的，但是排序后其顺序不可改变。
2. 设定初始阈值T1、T2，且T1 > T2。
3. 从数据集中随机取一个点作为中心点，计算其与其他点的距离，若距离小于T1但大于T2，则认为与其计算的点属于这个中心点所在的Canopy集内；若距离小于T2，则认为与其计算的点与中心点距离过近，不适宜再做中心点，于是将其从列表中删除。
4. 重复2、3步直到清空数据集。
5. 这时会得出n个中心点，通常将这n个中心点作为k-means算法的初始中心点，n为初始K
   遍历n个中心点所在的簇，如果某一簇的点的数量少于一定数目，则认为此处存在噪声点，因此直接删除此中心点和其所在的簇

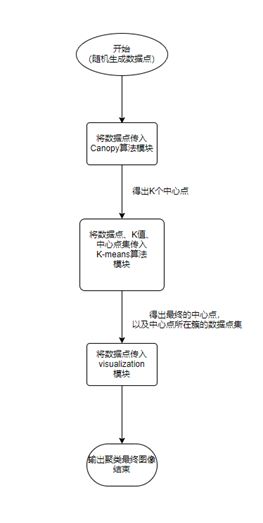
算法流程设计

算法的具体代码

Main类

from kmeans import k_means, canopy, visualization
import random
import numpy as np


points = []
center_points = []
K = 0
for i in range (0, 100):
    x = random.randint(0, 100)
    y = random.randint(0, 100)
    point = [x, y]
    points.append(point)
points = np.array(points)
# print(points)

canopy = canopy.Canopy(points, t1=75, t2=50)
canopy_cluster = canopy.find_cluster_by_canopy()
for i in canopy_cluster:
    center_points.append(i[0].tolist())
print("中心点集：", end=" ")
print(center_points)
K = len(center_points)

# for i in range (0, 4):
#     x = random.randint(0, 100)
#     y = random.randint(0, 100)
#     point = [x, y]
#     center_points.append(point)
kmeans = k_means.KMeans(points, center_points, K)
center_points, kmeans_cluster = kmeans.find_cluster_by_kmeans()
# print("更新后的中心点集：", end=" ")
print(center_points)
for i in kmeans_cluster:
    print(i)

visual = visualization.Visualization(center_points, kmeans_cluster)
visual.visual()

canopy类

import numpy as np
import math

class Canopy:
    dataset = []
    t1 = 0
    t2 = 0

    def __init__(self, dataset, t1, t2):
        self.dataset = dataset
        self.t1 = t1
        self.t2 = t2

    def euclidean_distance(self, point1, point2):
        return math.sqrt(pow(point1[0]-point2[0], 2) + pow(point1[1]-point2[1], 2))

    def get_index(self):
        return np.random.randint(len(self.dataset))

    def find_cluster_by_canopy(self):
        canopy_cluster = []
        while(len(self.dataset) != 0):
            center_set = []
            delete_set = []
            index = self.get_index()
            center_point = self.dataset[index]
            self.dataset = np.delete(self.dataset, index, 0)
            for i in range(len(self.dataset)):
                point = self.dataset[i]
                distance = self.euclidean_distance(point, center_point)
                if distance < self.t1:
                    center_set.append(point)
                if distance < self.t2:
                    delete_set.append(i)
            self.dataset = np.delete(self.dataset, delete_set, 0)
            canopy_cluster.append((center_point, center_set))
            canopy_cluster = [cluster for cluster in canopy_cluster if len(cluster[1]) > 1]
        return canopy_cluster

kmeans类

import math

class KMeans:
    dataset = []
    center_pointset = []
    K = 0

    def __init__(self, dataset, center_pointset, K):
        self.dataset = dataset
        self.center_pointset = center_pointset
        self.K = K

    def euclidean_distance(self, point1, point2):
        return math.sqrt(pow(point1[0]-point2[0], 2) + pow(point1[1]-point2[1], 2))

    def set_euclidean_distance(self, set1, set2):
        if len(set1) == 0 or len(set2) == 0:
            return 1
        flag = 0
        for i in range(len(set1)):
            if self.euclidean_distance(set1[i], set2[i]) != 0:
                flag = 1
                break
        return flag

    def find_center_point(self, list):
        xsum = 0
        ysum = 0
        length = len(list)
        for data in list:
            xsum += data[0]
            ysum += data[1]
        return [xsum // length, ysum // length]

    def find_cluster_by_kmeans(self):
        kmeans_clusters = []
        count = 0
        old_center_pointset = self.center_pointset
        new_center_pointset = []
        flag = self.set_euclidean_distance(old_center_pointset, new_center_pointset)
        while count < 50 and flag != 0:
            if count != 0:
                old_center_pointset = new_center_pointset
            kmeans_clusters = [[] for _ in range(self.K)]
            for data in self.dataset:
                dist = []
                for i in range(len(old_center_pointset)):
                    distance = self.euclidean_distance(data, old_center_pointset[i])
                    dist.append(distance)
                kmeans_clusters[dist.index(min(dist))].append(data.tolist())
            count += 1
            new_center_pointset = []
            for cluster in kmeans_clusters:
                new_center_pointset.append(self.find_center_point(cluster))
            flag = self.set_euclidean_distance(old_center_pointset, new_center_pointset)
            print("更新后的中心点集：", end=" ")
            print(new_center_pointset)
        return new_center_pointset, kmeans_clusters

visualization类

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号


class Visualization:
    center_points = []
    kmeans_cluster = []

    def __init__(self, center_points, kmeans_cluster):
        self.center_points = center_points
        self.kmeans_cluster = kmeans_cluster

    def format_point(self):
        lenth = len(self.kmeans_cluster)
        x_center_point = []
        y_center_point = []
        x_points = [[] for _ in range(lenth)]
        y_points = [[] for _ in range(lenth)]
        for center_point in self.center_points:
            x_center_point.append(center_point[0])
            y_center_point.append(center_point[1])
        for points in range(lenth):
            for point in self.kmeans_cluster[points]:
                x_points[points].append(point[0])
                y_points[points].append(point[1])
        return x_center_point, y_center_point, x_points, y_points

    def visual(self):
        x_center_point, y_center_point, x_point, y_point = self.format_point()
        fig, ax = plt.subplots()
        colors = ['r', 'g', 'b', 'y', 'c', 'm']
        for i in range(len(x_point)):
            ax.scatter(x_point[i], y_point[i], c=colors[i])
        ax.scatter(x_center_point, y_center_point, marker='*', s=200, c='black')
        plt.show()

四．算法测试结果

在具体的实验过程中，Canopy算法参数的设置上，我将T1设置为75，T2设置为50，这样Canopy生成的中心点数量基本是4个，也有少数生成5个中心点的情况出现。为了进行算法性能的对比，我将算法分为了两组，一组是直接随机生成K个中心点，我将K设置为4；一组是通过Canopy算法生成K个中心点。
我分别对两组进行了20次的重复实验，得出的k-means的中心点迭代次数如下表：

第一组的代表结果（背景图是我自己的pycharm壁纸，和本算法无关）：

第二组的代表结果：

从以上的结果可以看出，通过Canopy算法和k-means算法的结合，数据的聚类取得了良好的效果，并且有了Canopy算法帮助，使得k-mean在进行中心点的迭代次数大大减少（不使用时20次的重复实验得出的迭代次数平均值为11.35次，使用Canopy算法之后迭代次数的平均值降低到4次）。