R语言课程设计之-深圳房价预测模型

R语言课程设计之-深圳房价预测模型

目录
一、 摘要： 3
二、 R语言简介 3
三、 商品房价和时间的非线性模型 3
(一) 数据准备（导入数据）: 3
(二) 建立非线性模型 4
四、 影响房价的多因素的多元线性回归模型 6
(一) 模型的建立 6
(二) 模型的求解 7
(三) 模型总结 13
五、 房价预测及模型的对比评价 13
(一) 指数方程预测房价 13
(二) 多元线性回归预测房价 13
六、 总结 14
(一) 建议 14
(二) 心得 14
(三) 参考文献 14
摘要：
利用 R 语言优秀的统计计算和统计制图特点,对多元统计模型进行 分析。本文建立的模型主要是讨论深圳商品房的房价问题。
本文的数据来源于《深圳统计年鉴2019》和国家统计局，其中本文选取了比较接近现如今的2010-2018年的数据。考虑到商品房不同于一般商品，它不仅提供居住功能，同时还能带来收租收益，或产生增值活动。因此，在对当前深圳房价进行预测时，本文主要从深圳生产总值，在岗职工平均工资，年末人口，社会商品零售总额，商品房销售面积，房地产开发商业用房投资额六个方面来考虑对于商品房房价的影响。
R语言简介
R是用于统计分析、绘图的语言和操作环境。R是属于GNU系统的一个自由、免费、源代码开放的软件，它是一个用于统计计算和统计制图的优秀工具。
R是一套完整的数据处理、计算和制图软件系统。其功能包括：数据存储和处理系统；数组运算工具（其向量、矩阵运算方面功能尤其强大）；完整连贯的统计分析工具；优秀的统计制图功能；简便而强大的编程语言：可操纵数据的输入和输出，可实现分支、循环，用户可自定义功能。
与其说R是一种统计软件，还不如说R是一种数学计算的环境，因为R并不是仅仅提供若干统计程序、使用者只需指定数据库和若干参数便可进行一个统计分析。R的思想是：它可以提供一些集成的统计工具，但更大量的是它提供各种数学计算、统计计算的函数，从而使使用者能灵活机动的进行数据分析，甚至创造出符合需要的新的统计计算方法。
商品房价和时间的非线性模型
数据准备（导入数据）:
为了方便展示，我们分别为本文选取的六个因素设置为：
t：时间, y商品房平均销售价格, x1深圳生产总值, x2在岗职工平均工资, x3年末人口, x4社会商品零售总额, x5商品房销售面积, x6房地产开发商业用房投资额。
代码如下:

sz<-read.csv(“file:///C:/Users/admin/Desktop/price forecast.csv”,header = T,row.names=1)
show(sz)

数据如图:

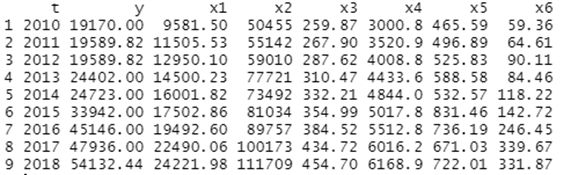
建立非线性模型
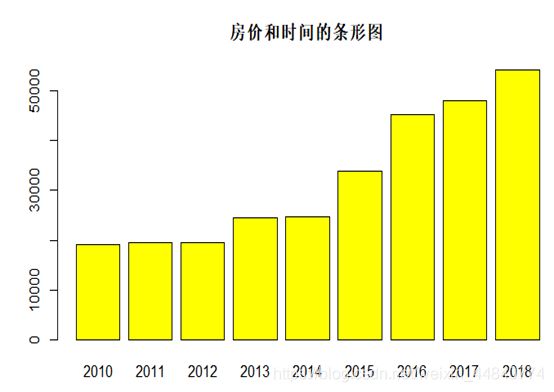
首先画出y关于t的条形图，代码如下:
newdata <-sz[,c(1,2)]
barplot(newdata$y,newdata$t,names.arg=t,col = “yellow”,main = “房价和时间的条形图”)
绘制条形图：

然后画出y关于t的散点图，代码如下:
plot(t,y)
绘制散点图:

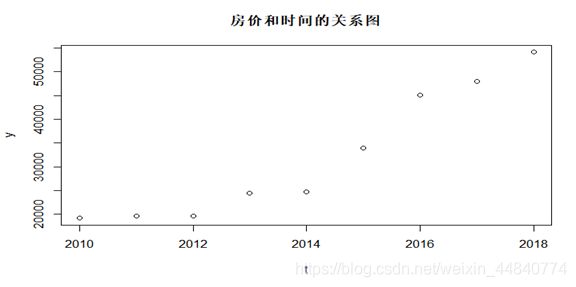
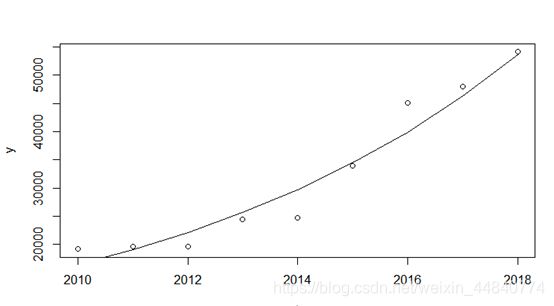
由散点图可知，初步认为y与t成指数关系，利用R语言进行拟合检验。对指数函数y=ae^bt两边取自然对数得：lny=lna+bt，令y_1=lny，a_1=lna则可将其化为一元线性函数y_1=a_1+bt对y取对数并进行一元线性回归的R语言程序为：
y1=log(y)
reg=lm(y1~t)
summary(reg)
得到结果为：

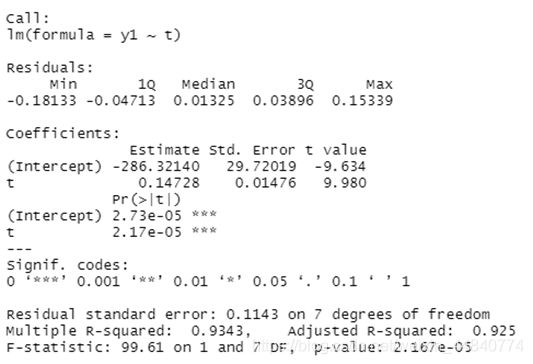
则可知常数项a_1=-286.32140，变量系数b=0.14728得到回归方程如下： y_1=-286.3214+0.14728t
将a=e^a1得到a的值为4.489479e-125，得到y关于t的指数方程为：
y=( 4.489479e-125)exp(0.14728t)
将得到的曲线与原散点图进行比较，代码为：
plot(t,y)
a1=-286.32140
a=exp(a1)
b=0.14728
yy=aexp(bt)
lines(t,yy)

如图：

影响房价的多因素的多元线性回归模型
模型的建立
y商品房平均销售价格；x1深圳生产总值；x2在岗职工平均工资；x3年末人口；x4社会商品零售总额,；x5商品房销售面积,；x6房地产开发商业用房投资额。则建立这6个关于y的多元线性回归模型：
y=β_0+β_1 x_1+β_2 x_2+β_3 x_3+β_4 x_4+β_5 x_5+β_6 x_6+ε
公式中的：β_0，β_1，β_3，β_4，β_5，β_6为未知参数，ε为随机误差，且认为ε服从正太分布。对于公式中未知参数的估计采用最小二乘法，求相关系数R^2，并做显著性检验，证明模型的建立是正确的。
模型的求解
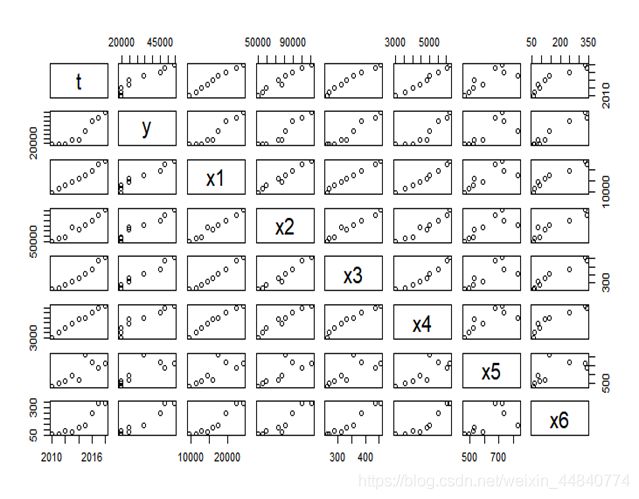
为了确定商品房销售价格与各变量之间的关系，分别作出y与x_i
的散点图，代码如下：
plot(sz)
如图：

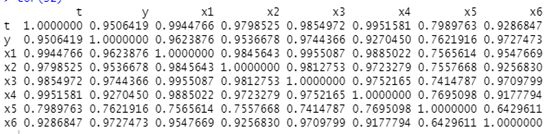
利用cor（sz）得到相关矩阵并整理得：

并分别对y与x_i的相关性进行检验，检验代码如下：
cor.test(y,x1)
cor.test(y,x2)
cor.test(y,x3)
cor.test(y,x4)
cor.test(y,x5)
cor.test(y,x6)
得到结果如下：

综上结果可知，在α=0.05的条件下,六个变量与y的性关系都较好。
对六个变量进行多元回归方程，代码如下：

reg1=lm(y~x1+x2+x3+x4+x5+x6)
summary(reg1)
结果如下图：

图7 多元回归分析结果
对系数进行显著性检验，由结果可知，β_0，β_1，β_3，β_4，β_5，β_6的P值均大于0.05，故不能拒绝原假设，认为这些变量效果不明显，可以认为这些系数为零
对方程进行检验，残差的标准差为2929,而相关系数R^2=0.9544，P值小于0.05，效果明显，故拒绝原假设，即认为y与各个变量之间存在线性关系。 
根据P值，选择剔除一个变量，对回归模型进行优化，故剔除x1,则reg2=lm(y~x2+x3+x4+x5+x6)
Summary(reg2)
结果如下：

对方程进行检验，残差的标准差为2396,而相关系数R^2=0.9695，P值小于0.05，效果明显，故拒绝原假设，即认为y与剔除x1后的变量之间存在线性关系。
根据P值，选择剔除一个变量，对回归模型进行优化，故剔除x3，则：reg3=lm(y~x2+x4+x5+x6)
summary(reg3)
结果如下：

对方程进行检验，残差的标准差为2093,而相关系数R^2=0.9767，P值小于0.05，效果明显，故拒绝原假设，即认为y与剔除x1和x3后的变量之间存在线性关系。
根据P值，选择剔除一个变量，对回归模型进行优化，故剔除x4，则：reg4=lm(y~x2+x5+x6)
summary(reg4)

结果如下

对方程进行检验，残差的标准差为2414,而相关系数R^2=0.969，P值小于0.05，效果明显，故拒绝原假设，即认为y与剔除x1、x3和x4后的变量之间存在线性关系。
继续剔除x2：
reg5=lm(y~x5+x6)
summary(reg5)
结果如图：

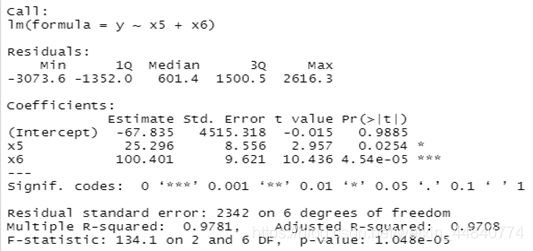
对系数进行显著性检验，由结果可知，β_5，β_6在0.05条件下，均拒绝原假设，认为具有很好的效果。
对方程进行检验，残差的标准差为2342,而相关系数R^2=0.9708，P值小于0.05，效果明显，故拒绝原假设，即认为y与各变量之间存在线性关系。
模型总结
通过5次回归，最终得到最优的多元线性模型为：
y=-67.835+25.296x5+100.401x6
从该模型分析可知，在所选的因素中，只有x5商品房销售面积和x6房地产开发商业用房投资额被保留下来，而x1深圳生产总值, x2在岗职工平均工资,x3年末人口, x4社会商品零售总额被剔除。
房价预测及模型的对比评价
指数方程预测房价
本文共预测得到两个预测模型及其预测值为：
y关于t的指数方程为：
y=( 4.489479e-125)exp(0.14728t)
对y进行预测的代码为：
tt=2019:2021
yy=aexp(btt)
yy
运行结果为：[1] 62126.01 71984.06 83406.37
可见2019-2021年的预测值分别为：62126.01、71984.06、83406.37。其中2019年均价62126.01元与网络流传的深圳商品房均价65516元（非官方）相差不大，偏差比例为5.17%。附图：

多元线性回归预测房价
Y关于影响因素的多元线性回归模型：
y=-67.835+25.296x5+100.401x6
预测值与收集的实际数据对比如下图：

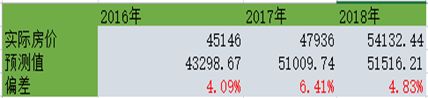
可知多因素线性回归模型有较好的预测值，预测偏差均较小。
总结
建议
根据房价时间模型，房价将随着时间呈指数增长之势，因此必须出台相关政策，有效抑制房价增长。根据多元线性模型，房价与各个自变量的正负相关性就是各个变量前系数的正负。要抑制房价的增长，可以通过使系数为正的自变量增长率减少，系数为负的自变量增长率增加来达到目的。
心得
学习一个软件，并将其应用于实践，可以快速提高软件的应用能力和对软件的理解。本文从用R语言读入数据表，到做初步的相关分析和一元非线性和多元线性回归，各个步骤的实施，对R语言基本操作和软件包有了一个更深入的了解和认识，为进一步的学习打下了基础。另外，在学习的时候，要从资料中进行学习和归纳，将各个方法用R语言去实践，多多使用，只有日积月累才能日渐精深。
对于模型的建立方面：在自变量的选择上虽然查找了相关的资料，但是考虑可能仍然有所欠缺，而且从其相关分析图可知，6个自变量并不是相互独立的，这使得最后得出房价与各自变量的正负相关性有误差。
参考文献
Robert I.Kabacoff[美].R语言实战（第二版），2016
（来源于国家统计局和《深圳统计年鉴2019》）

关注公众号，发送“r模型”获取数据，代码等资料，自己亲自试一试吧！！！
如果觉得有用的就点个赞吧(#.#)