浅析网格数据np.meshgrid()及等高线plt.contour()原理
在做支持向量机决策边界绘制时,或多或少都会遇到这两个问题。
1.当我们将两个一维数组传入np.meshgrid()后,它的内部是怎么实现的?
2.当我们准备好的数据放入plt.contour()后,他是如何绘制等高线的?
在这过程中我们用到两个包:
import matplotlib.pyplot as plt
import numpy as np
准备数据:
x = np.linspace(-2, 2, 5)
y = np.linspace(-2, 2, 5)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2 - 1
接下来我们看一下,np.meshgrid()将我们的x, y转成什么样的网格了。
数据如下:
x: [-2. -1. 0. 1. 2.]
y: [-2. -1. 0. 1. 2.]
网格数据X.shape为(5, 5),数据内容如下:
[[-2. -1. 0. 1. 2.]
[-2. -1. 0. 1. 2.]
[-2. -1. 0. 1. 2.]
[-2. -1. 0. 1. 2.]
[-2. -1. 0. 1. 2.]]
网格数据Y.shape为(5, 5),数据内容如下:
[[-2. -2. -2. -2. -2.]
[-1. -1. -1. -1. -1.]
[ 0. 0. 0. 0. 0.]
[ 1. 1. 1. 1. 1.]
[ 2. 2. 2. 2. 2.]]
通过观察我们发下,经过X, Y = np.meshgrid(x, y)操作,它将我们的x数据纵向复制了5份,而将Y 转置之后横向复制了5份。那么它复制的个数5是按照自己的长度呢?还是另一个坐标的数结构呢?通过下面例子可知:
x = [1, 2]
y = [3, 4, 5]
X, Y = np.meshgrid(x, y)
print(X)
print(Y)
控制台输出:
[[1 2]
[1 2]
[1 2]]
[[3 3]
[4 4]
[5 5]]
另一个问题,这样做是什么原理?既然说np.meshgrid()做出来的数据是网格数据,那么我们将X, Y 绘制出来看看:
plt.figure(figsize=(6, 4))
ax1 = plt.gca()
ax2 = plt.gca()
ax1.vlines(x=X, ymin=Y[0], ymax=Y[4], colors='r', linestyles='-.', linewidth=0.5)
ax2.hlines(y=X, xmin=Y[0], xmax=Y[4], colors='g', linestyles='-.', linewidth=0.5)
plt.scatter(X, Y)
我们分别单独观察X,Y以及X,Y的组合图:
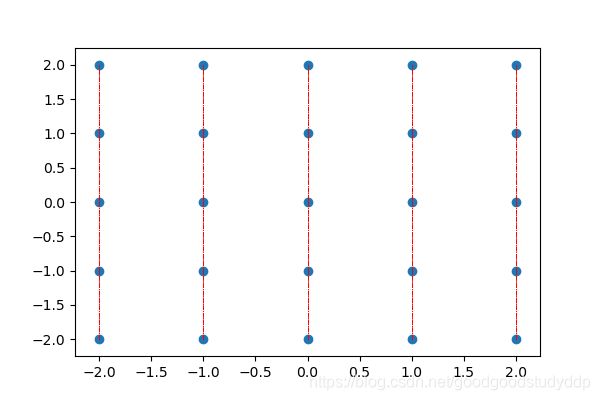
上图即是x: [-2. -1. 0. 1. 2.]数据纵向复制5份的效果即为X。
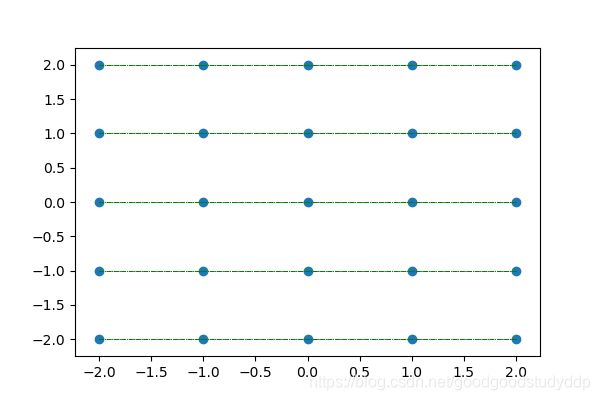
上图即是y: [-2. -1. 0. 1. 2.]数据转置后横向复制5份的效果即为Y。
下面是X, Y 的组合效果:

我们发下,np.meshgrid()真的将我们的x, y数据做成了网格。而X, Y矩阵对应位置的数据就是图中相应位置点的坐标。而且,网格形状也是(5 x 5)。
接下来我们谈谈等高线。什么是等高线:把地面上海拔高度相同的点连成的闭合曲线,并垂直投影到一个水平面上,并按比例缩绘在图纸上,就得到等高线。一句话说就是再一个平面上将使得Z = f(x, y)的Z值相等的众多坐标点(注意:不止一个坐标点,这一点后边会有所体现。)相连即为高度值为Z的等高线。
OK,上述生成的网格那么优美,我们必须得搭配一个更优美的曲线x^2 + y^2= 1 来做我们的等高线喽。即Z = f(x, y) = x^2 + y^2 - 1。
将我们的X, Y带入f(X, Y)得到Z形式也是(5x5),数据如下:
[[ 7. 4. 3. 4. 7.]
[ 4. 1. 0. 1. 4.]
[ 3. 0. -1. 0. 3.]
[ 4. 1. 0. 1. 4.]
[ 7. 4. 3. 4. 7.]]
如果仔细观察,你会发现Z的形状与X,Y的形状相同,更更更重要的是,Z的形状与我们的网格图相对应(不是噎住了, 为了强调这种对应关系对生成等高线的重要性)!
接下来呢?上代码+图,生成我们的等高线:
ax = plt.gca()
cor = ax.contour(X, Y, Z, [-1, 0, 1, 3])
plt.clabel(cor, fontsize=10)
plt.show()
生成图:
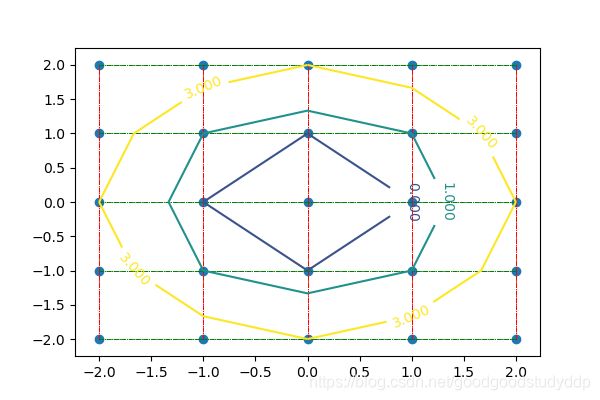
最后,但不是最不重要的是:我们指出让在 [-1, 0, 1, 3]四个等高线上下标签,但是-1没有被写出来???
如果我们只写[-1],会出现如下警告:
UserWarning: No contour levels were found within the data range.
cor = ax.contour(X, Y, Z, [-1])
此处,与前面某处呼应,即只有不止一个点带入f(x, y)中有相同值时,等高线才产生!
OK,Class is over.