智能优化算法:海鸥优化算法-附代码
2019智能优化算法:海鸥优化算法-附代码
文章目录
- 2019智能优化算法:海鸥优化算法-附代码
-
- 1.原理
- 2.SOA算法
-
- 1.迁徙 ( 全局搜索 )
- 2.攻击 ( 局部搜索 )
- 3.算法伪代码:
-
- 1.主程序框架
- 2.计算适应值 (P s ) 过程
- 3.更新最佳海鸥位置和适应值过程
- 3.运行结果图:
- 4.参考文献:
- 5.Matlab代码地址:[https://mianbaoduo.com/o/bread/Z5WVlZs=](https://mianbaoduo.com/o/bread/Z5WVlZs=)
- 6. Python代码
摘要:本文简单介绍智能优化算法-海鸥优化算法[1][2]
1.原理
海鸥是遍布全球的海鸟,海鸥种类繁多且大小和身长各不相同。 海鸥是杂食动物,吃昆虫、鱼、爬行动物、两栖动物和蚯蚓等。 大多数海鸥的身体覆盖着白色的羽毛,经常用面包屑来吸引鱼群, 用脚发出雨水落下的声音来吸引藏在地下的蚯蚓。海鸥可以喝淡水和盐水,通过眼睛上方的一对特殊腺体,将盐从它们的体内排出。 海鸥以群居式生活,利用智慧来寻找和攻击猎物。 海鸥最重要特征是迁徙和攻击行为,迁徙是动物从一个地方到另一个地方根据季节更替而移动,寻找最丰富的食物来源以便获取足够能量。在迁移期间,动物成群结队地出行。迁徙时每只海鸥的所在位置不同,以避免相互碰撞。 在一个群体中,海鸥可以朝着最佳位置的方向前进,改变自身所在的位置。海鸥经常会攻击候鸟,在进攻时海鸥群体做出螺旋形的运动形态(如图1)。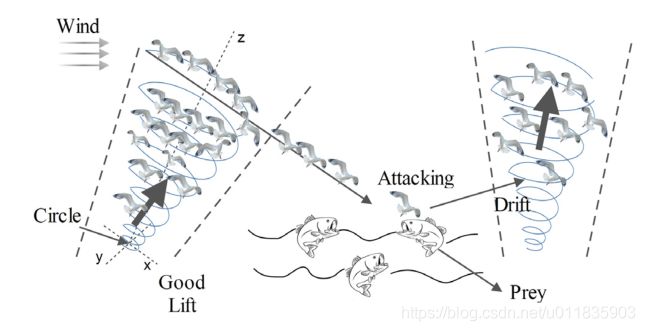
图1.海鸥迁徙和攻击方式示意图
2.SOA算法
1.迁徙 ( 全局搜索 )
在迁移过程中, 算法模拟海鸥群如何从一个位置移动到另一个位置。 在这个阶段,海鸥应该满足三个条件:避免碰撞:为了避免与邻居 ( 其他海鸥 ) 碰撞,算法采用附加变量 A 计算海鸥的新位置。
C s ( t ) = A ∗ P s ( t ) C_{s}(t) = A*P_{s}(t) Cs(t)=A∗Ps(t)
C s ( t ) C_{s}(t) Cs(t)表示不与其他海鸥存在位置冲突的新位置, P s ( t ) P_{s}(t) Ps(t)海鸥当前位置, t 表示当前迭代, A 表示海鸥在给定搜索空间中的运动行为。
A = f c − ( t ∗ ( f c / M a x i t e r a t i o n ) ) A = f_{c}-(t*(f_{c}/Max_{iteration})) A=fc−(t∗(fc/Maxiteration))
f c f_{c} fc可以控制变量 A 的频率,它的值从 2 线性降低到 0 。
最佳位置方向:在避免了与其他海鸥的位置重合之后,海鸥会向最佳位置所在的方向移动。
M s ( t ) = B ∗ ( P b s ( t ) − P s ( t ) ) M_{s}(t)=B*(P_{bs}(t)-P_{s}(t)) Ms(t)=B∗(Pbs(t)−Ps(t))
M s ( t ) M_{s}(t) Ms(t)表示最佳位置所在的方向, B 是负责平衡全局和局部
搜索的随机数。
B = 2 ∗ A 2 ∗ r d B=2*A^{2}*r_{d} B=2∗A2∗rd
r d r_{d} rd是 [0 , 1] 范围内的随机数。
靠近最佳位置 : 海鸥移动到不与其他海鸥相撞的位置后,就
向着最佳位置的所在方向进行移动,到达新的位置。
D s ( t ) = ∣ C s ( t ) + M s ( t ) ∣ D_{s}(t)=|C_{s}(t)+M_{s}(t)| Ds(t)=∣Cs(t)+Ms(t)∣
D s ( t ) D_{s}(t) Ds(t)是海鸥的新位置。
2.攻击 ( 局部搜索 )
海鸥在迁徙过程中可以不断改变攻击角度和速度, 它们用翅膀和重量保持高度。当攻击猎物时,它们就在空中进行螺旋形状运动。 x 、 y 和 z 平面中的运动行为描述如下:
x = r ∗ c o s ( θ ) y = r ∗ s i n ( θ ) z = r ∗ θ r = u ∗ e θ v x=r*cos(\theta)\\ y=r*sin(\theta)\\ z=r*\theta\\ r=u*e^{\theta v} x=r∗cos(θ)y=r∗sin(θ)z=r∗θr=u∗eθv
其中 r 是每个螺旋的半径, θ 是 [0 , 2π] 范围内的随机角度
值。u 和 v 是螺旋形状的相关常数, e 是自然对数的底数。海鸥的
攻击位置前面的式子可得:
P s ( t ) = D s ( t ) ∗ x ∗ y ∗ z + P b s ( t ) P_{s}(t)=D_{s}(t)*x*y*z+P_{bs}(t) Ps(t)=Ds(t)∗x∗y∗z+Pbs(t)
P s ( t ) P_{s}(t) Ps(t)是海鸥的攻击位置。
3.算法伪代码:
1.主程序框架
( 1 ) 海鸥种群 P s P_{s} Ps 初始化,参数 A A A 、 B B B 和 M A X i t e r a t i o n MAX_{iteration} MAXiteration。
( 2 ) 设置相应参数: f c f_{c} fc = 2, u = 1 u=1 u=1, v = 1 v=1 v=1。
( 3 ) W h i l e ( t < 最 大 迭 代 次 数 ) While(t < 最大迭代次数) While(t<最大迭代次数)
( 4 ) { 计算适应值 ( P s P_{s} Ps ) /* 使用计算适应度函数计算每只海鸥的适应度值 */
( 5 ) r d r_{d} rd 取随机值 (0 , 1)
( 6 ) θ \theta θ 取随机值 (0 , 2π)
( 7 ) r = u ∗ e θ v r=u*e^{\theta v} r=u∗eθv
( 8 )计算 D s D_{s} Ds
( 9 )计算海鸥新位置 P s P_{s} Ps
( 10 )更新最佳海鸥位置和适应值, t = t + 1 t=t+1 t=t+1;
( 11 ) }
( 12 )输出最佳海鸥位置和适应值,结束程序
2.计算适应值 (P s ) 过程
( 1 ) for i=1 to n
( 2 ) {
( 3 )计算每只海鸥适应值
( 4 ) }
( 5 )更新最佳海鸥位置和适应值
( 6 )输出最佳海鸥适应值
( 7 )结束
3.更新最佳海鸥位置和适应值过程
( 1 ) for i=1 to n
( 2 ) {
( 3 )如果海鸥 (i) 的适应值小于 Best 值
( 4 ) { 用海鸥 (i) 的适应值替代 Best 值
( 5 )用海鸥 (i) 的位置替代 Best 的位置
( 6 ) }
( 7 ) }
( 8 )输出 Best 值和位置
( 9 )结束程序
3.运行结果图:
4.参考文献:
[1]韩毅,徐梓斌,张亮,邓丽丽.国外新型智能优化算法——海鸥优化算法[J].现代营销(经营版),2019(10):70-71.
[2]Gaurav Dhiman,Vijay Kumar. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems[J]. Knowledge-Based Systems,2018.
5.Matlab代码地址:https://mianbaoduo.com/o/bread/Z5WVlZs=
6. Python代码
https://mianbaoduo.com/o/bread/aZuTlJY=
