你不知道的Redis八-Redis底层数据结构解析

目录

一、Redis存储的数据的数据结构

二、Redis中键和值得数据结构

1、redis键值的数据结构

2、hash冲突

3、rehash阻塞

4、渐进式rehash

二、压缩列表

三、跳表

四、rdis使用建议

---

一、Redis存储的数据的数据结构

我们都只到Redis常用的数据结构为String，List，Hash，Set，Sorted Set。但这只是我们在用的时候键值对的表现形式，他们底层真正使用的数据结构为简单动态字符串，双向链表，压缩列表，哈希表，调表和整数数组

 

可以看到，String 类型的底层实现只有一种数据结构，也就是简单动态字符串。而 List、Hash、Set 和 Sorted Set 这四种数据类型，都有两种底层实现结构。通常情况下，我们会把这四种类型称为集合类型，它们的特点是一个键对应了一个集合的数据

二、Redis中键和值得数据结构

1、redis键值的数据结构

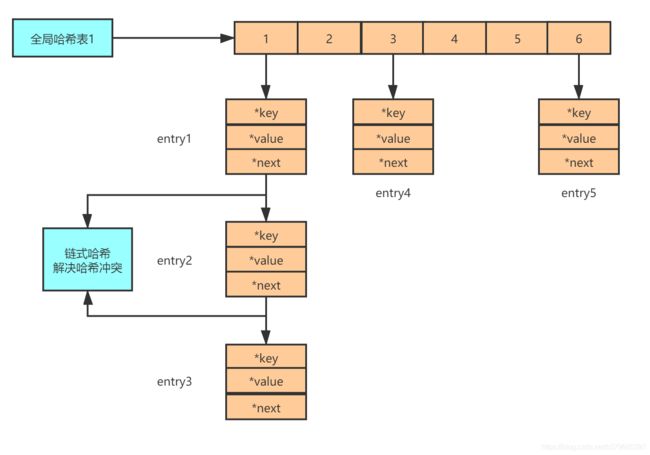
因为redis本身要求获取速度快，那么时间复杂度肯定是O1，为了实现从键到值的快速访问，Redis 使用了一个哈希表来保存所有键值对。数据结构如下

 

redis是由一个全局hash表存储所有键和值得关系。值存的为对象的地址。

2、hash冲突

既然使用hash表，那么就肯定会有hash冲突。Redis 解决哈希冲突的方式，和JAVA中的hash表解决方式一样，也是链式哈希。链式哈希也很容易理解，就是指同一个哈希桶中的多个元素用一个链表来保存，它们之间依次用指针连接。

 

因此当Key特别大的时候，存在着链式查找的一个时间消耗。特别是当我们存在几千万key的时候，那这个时间消耗也是非常多的

 

3、rehash阻塞

为了解决hash冲突带来的链表长度太长，因此redis引入对hash的rehash操作

rehash 也就是增加现有的哈希桶数量，让逐渐增多的 entry 元素能在更多的桶之间分散保存，减少单个桶中的元素数量，从而减少单个桶中的冲突。

具体操作

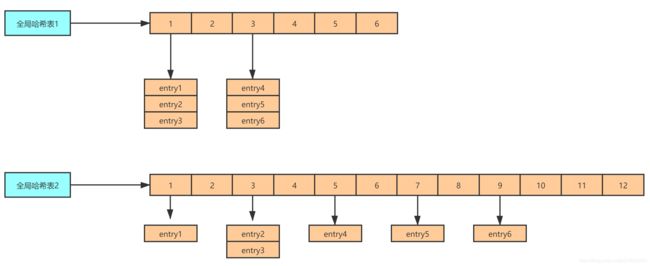
Redis 默认使用了两个全局哈希表：哈希表 1 和哈希表 2。一开始，当你刚插入数据时，默认使用哈希表 1，此时的哈希表 2 并没有被分配空间。随着数据逐步增多，Redis 开始执行 rehash，这个过程分为三步：

1、给哈希表 2 分配更大的空间，例如是当前哈希表 1 大小的两倍；

2、把哈希表 1 中的数据重新进行打散映射到hash表2中；

3、释放哈希表 1 的空间。

我们就可以从哈希表 1 切换到哈希表 2，用增大的哈希表 2 保存更多数据，而原来的哈希表 1 留作下一次 rehash 扩容备用

这个过程看似简单，但是第二步涉及大量的数据拷贝，如果一次性把哈希表 1 中的数据都迁移完，会造成 Redis 线程阻塞，无法服务其他请求。此时，Redis 就无法快速访问数据了。

为了避免这个问题，Redis 采用了渐进式 rehash。

4、渐进式rehash

简单来说就是在第二步拷贝数据时，Redis 仍然正常处理客户端请求，每处理一个请求时，从哈希表 1 中的第一个索引位置开始，顺带着将这个索引位置上的所有 entries 拷贝到哈希表 2 中；等处理下一个请求时，再顺带拷贝哈希表 1 中的下一个索引位置的 entries。如下图所示：

这样就巧妙地把一次性大量拷贝的开销，分摊到了多次处理请求的过程中，避免了耗时操作，保证了数据的快速访问。

二、压缩列表

之前也说了，集合类型的底层数据结构主要有 5 种：整数数组、双向链表、哈希表、压缩列表和跳表。其中,哈希表刚才已经讲过，整数数组、双向链表也比较常见。那么我们具体看下压缩列表和跳表

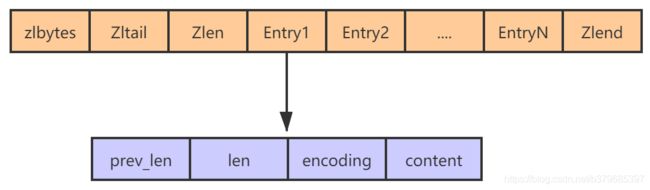
zlbytes:记录压缩列表占用的内存字节数，对压缩列表进行内存重分配或者计算zlen位置时使用，占用4个字节

Zltail：记录也锁列表未节点距离压缩列表的起始节点有多少字节，通过这个偏移量，程序无需便利整个压缩列表就可以确定表尾节点的位置 占用4个字节

Zllen:记录列表包含的节点数量，占用2个字节

Zllend:记录压缩列表的末端，占用1个字节

entry：压缩列表保存的数据，主要有以下属性

• prev_len，表示前一个 entry 的长度。prev_len 有两种取值情况：1 字节或 5 字节。取值 1 字节时，表示上一个 entry 的长度小于 254 字节。虽然 1 字节的值能表示的数值范围是 0 到 255，但是压缩列表中 zlend 的取值默认是 255，因此，就默认用 255 表示整个压缩列表的结束，其他表示长度的地方就不能再用 255 这个值了。所以，当上一个 entry 长度小于 254 字节时，prev_len 取值为 1 字节，否则，就取值为 5 字节。
• len：表示自身长度，4 字节；
• encoding：表示编码方式，1 字节；
• content：保存实际数据。

如果我们要查找定位第一个元素和最后一个元素，可以通过表头三个字段的长度直接定位，复杂度是 O(1)。而查找其他元素时，就没有这么高效了，只能逐个查找，此时的复杂度就是 O(N) 了。

三、跳表

有序链表只能逐一查找元素，导致操作起来非常缓慢，于是就出现了跳表。具体来说，跳表在链表的基础上，增加了多级索引，通过索引位置的几个跳转，实现数据的快速定位。

如果我们使用上图所示的跳跃表，就可以减少查找所需时间为O(n/2)，因为我们可以先通过每个节点的最上面的指针先进行查找，这样子就能跳过一半的节点。

比如我们想查找50，首先和20比较，大于20之后，在和40进行比较，然后在和70进行比较，发现70大于50，说明查找的点在40和50之间，从这个过程中，我们可以看出，查找的时候跳过了30。

跳跃表其实也是一种通过“空间来换取时间”的一个算法，令链表的每个结点不仅记录next结点位置，还可以按照level层级分别记录后继第level个结点。此法使用的就是“先大步查找确定范围，再逐渐缩小迫近”的思想进行的查找。跳跃表在算法效率上很接近红黑树。

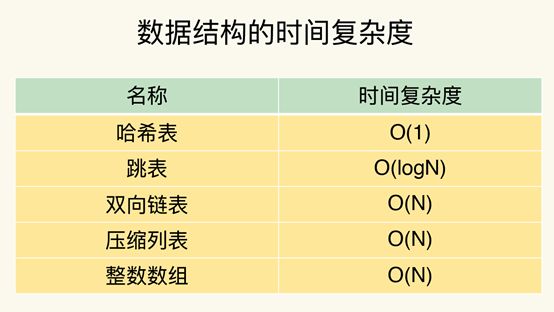
四、Redis数据结构时间复杂度

 

五、Redis使用建议

第一，对于单元素操作，对于redis的使用尽量使用单元素操作。这种效率一般都比较高。

第二，范围操作，是指集合类型中的遍历操作，可以返回集合中的所有数据，这类操作一般都比较耗时，尽量避免

第三，统计操作，是指集合类型对集合中所有元素个数的记录，因为这些数据结构本身记录所有元素个数，时间复杂度为O(1)所以效率很高

第四，例外情况，是指某些数据结构的特殊记录，例如压缩列表和双向链表都会记录表头和表尾的偏移量。对于头插和尾插增删元素可以通过偏移量直接定位，所以时间复杂度也是O(1)。实现快速操