智能时代的商业思维-笔记（未完）

学习 硅谷来信²·谷歌方法论

0.计算机思维与智能时代

智能时代

未来是基于数据的智能时代，越来越多的问题通过计算去解决，需要人的智慧+计算机的能力。

1.计算机解决问题的框架

1. 宏观:找到现实世界和虚拟世界的对应。
   a. 基于计算的边界
   可计算。如何使用计算机这个 工具,将虚拟世界处理问题的方法变成 解决现实生活中的各种实际问题的方法。
   b. 工具
   大数思维
2. 中观:在有限资源的情况下做到全局最优。
   a. 一个 好的操作系统,不是做某一件事特别 好,而是在资源有限的情况下整体上让 人感觉特别流畅。
   i. 计算机的解决方式最终是一套系统。
   1. 递归原 理归是计 算机科学的精髓。自顶向下设计,再自下而上 回归。它将大事分解、从小事做起,步步 干净利落,非常具有美感。
   ii. 任何操作系统都要求按照各项任务的优先级和可使用的资源,设计出调配资源、让计算机各部分协同工作的方法, 并且对于各种任务进行整体优化。
3. 微观:合理组织和利用资源,凡事留 有余地。
   a. 索引，设计出计算机内部整理和查找信息的 技能(addressing）。
   i. 计算机内外的各种资源都要合理地编号 存储,然后根据编号来访问,要有合理 的编号方案,以及与其配合的高效率访 问算法,这是实现计算机各种应用好坏 的关键。在生活中,它等同于我们处理 各种事情的条理性。
   b. 缓存。凡事要留有余量,很多时候要 预先准备好数据和程序,这就是缓存。

大数思维

1. 量级：从量级上评估解决问题的方法。
我们生活在小数字世界,从小数字世界 总结出来的方法论无法应用到更高量级 的大数世界，尤其是在计算机行业中。
	以排序算法为例，传统的排除和快速排序的在小数排序上计算量差不多的，当数据量为上亿时，计算量有量级的差别。
	商业思维：数量大小的认知决定了商业模式,也决了企斗的成败。
2. 

1.1大数与小数世界

小数字世界：人对大数无感。人类生活的环境,决定了我们对 大数字是无感的。习惯了某一个环境的度量,其实很难理解在量级上大得多的世界。
第一个例子,会做 PPT的人都知道 要用图表,而不是用数字列表来说明问 题,因为认知学家早就发现人对大数字 是无感的。今天很多人数100,000, 000这个数字,还是从后往前,个十百千 万地数。
第二个例子是王健林在2016年半开 玩笑地讲,“先定个小目标,比如说一个 亿”,被全社会吐槽,因为即便是在今天 的美国,也很少有人能一辈子挣一亿人 民币(也就是1400万美元左右)，对大 部分人来讲,一亿等于财富自由,等于 无穷大。

• 大数世界

  科技的进步对计算能力的要求，超出了人力范围。
  计算机时代数据量剧增的，超出人力，网页 数量从90年代初的几百万,增加到今天 的几百亿。现在人还可以通过算法来控制计算机，未来算法的负责可能也会超出人力，这就是大数据和智能。

• 计算机

  电脑一开始就是针对海量数字设计的，电脑的核心价值是补足人的计算能力，凭借的是进化速度。

  • 计算能力：
    1946年人类第一台电子计算机诞生 时,每秒钟能进行5000次运算。虽然这 个速度只有iPhone 计算速度的一百万分 |之一左右,但是比人已经快得不得了 了。2*10^172,对于人来说是无穷大，而对计算机来说却是一个可以计算的问题。当时科学家们让它计算长程火炮炮弹 的轨迹–这其实是发明电子计算机的原 始目的,炮弹还没有落地,计算机就算 出了轨迹,以至于在场的蒙巴顿元帅看 得目瞪口呆,说,真快啊,简直是电的 脑,"电脑"一词就是这么来的。

  • 数据量
    今天如果要开发 5年之后的 IT 产品,就必须假设在今天 10倍资源的框架下进行设计。Google真的是保存一切,索 引一切,它们在Google的数据中心中还 不止一个拷贝。

  • 进化速度
    在人的世界里,增长是缓慢
    人类对数字的认知也受 限于我们作为生物进化的速度,这是人的思维和计算机的思维的另一个不同之 处。
    世界上最早的农业大约始于1万年 前,人类大约从那个时代开始识数,人 类最早的计算工具（在兽骨上刻上划痕 计数）也始于那个年代。可以讲从酋长 们认识3,到今天我们认识一个亿,经历 了大约10000年的时间。平均每十年进步 干分之八,不到1%。另一方面人脑和其他灵长类的脑容量差距：？。
    计算机的进步速度有多快呢?
    这大约相当于每五年涨十 倍,或者每十年进步一百倍!摩尔定律让计算机每十八个月性 能翻一番,。Phone 8正好是第十年, Phone 8的速度恰巧大约是当初乔布斯宣 布的第一款 iPhone的100倍左右。

1.2计算机的边界

计算机只能解决确定性的问题
世界上只有一小部分问题是数学问题，而这部分有确定答案的也只是一小部分，这一下部分能够用确定步骤解决的才是计算机可以解决的问题，最后智能技术也只能解决部分计算机的问题。

图灵机的设计思路基于上述原理。而实现计算来自于确定性的机 械的运动。 电子计算机,里面电子 的运动其实等价于机械运动。图灵同时 猜测人的意识来自于测不准原理,这是 宇宙本身的规律。图灵从此得出结论, 计算是确定的,而意识可以是不定的, 两者不可能划等号

2.极限思维

3.数据结构

1. 数据结构是相互之间存在一种或多种特定关系的数据元素的集合，由逻辑结构和存储结构构成。安逻辑分为：线性和非线性
   a. 数据结构就是数据中常用的具体 关系。类似于美学中的构图法，程序中基本的几何图形,就是计算机的数据结构。如果说一 幅画是点的有机组合,几何图形反映出点之间 常用具体的关系,那么在计算机科学中,数据 就等同于点。
   b. 专业的计算机人士水平的高下,首先在于灵活使用这些数据结构的本领。数据结构没有学好,程序写得再快,也是业余 水平。
   世界界著名计算机科学家、因为发明帕斯卡 |程序语言(PASCAL）而获得图灵奖的N·沃斯 （N.Wirth)教授写过一本书,叫做《数据结构+ 算法=程序》,很好地讲清楚了这三者的关系。
2. 最常用的数据结构：线性表和二叉树
   a. 线性表
   ▪ 线性表是最基本的数据结构。最常见 的一种实现方法就是所谓的数组。本身是一个抽象的概念,在计算机 中则是通过很多种具体的方法实现的，相当于几何 图形中的直线
   1. 线性表这种抽象的数据结构起源于办公 自动化。
   早期商业上,报表是一种最常见的数据组织 形式,而在管理上,最多见的则是人员或者物 资的记录等等。它们都可以被抽象为线性的数 据,然后按照1、2、3、4、5的顺序排列出 来。因此,很有必要设计一种抽象的数据结构 概括所有这些顺序排列和储存的数据,它就是 线性表。
   随着计算机数据规模的扩张, 未必必能够给所有的数据都赋予一个编号顺序,结构化地存储,但是它们依然遵循一个顺序的 特征。比如一个电商交易的日志记录,它是按 照所发生的时间顺序,一条条线性地记录下 来,因此,线性表的性质它们也有
   ▪ 数组
   1. 数组，是有序的元素序列，编了号的 固定大小的单元。
   2. 好处：是给定一个 序号,可以直接找出里面的内容。
   a. 一个 数组存着一个单位员工的信息,只要给出员工 的工号,就能调出他的信息并且编辑修改。相当于盖房子的砖头,一块块整整 齐齐地码着
   b. 缺陷 ：在其中插入一个新的数据非常困难。
   i. 比 如客户经理用一个数组来存放这周要去拜访的 所有客户,如果他突然有一个未在计划中的客 户必须要拜访,他打算把这个人插入到原来第 五个客户和第六个客户之间。那么要在数组中 塞进去这个新的客户其实并不容易,因为他需 要把第六个客户从数组中的第六个位置挪到第 七个,留出位置给这个新的客户。当然,也就 |需要把第七个挪到第八个的位置,第八个挪到 |第九个的位置,以此类推。如果一个数组有上 百万个记录,这么挪实在是太浪费时间了。
   b. 链表的线性数据结构
   没有固定编号的数组，位置的确定是相对值
   i. 好处：插入更加方便。
   所谓链表,其实 就如同我们买东西时排队一样,每个人只要记 得前面或者后面的一个人是谁就可以了,彼此 没有编号一说。
   如要记录下这周造访的客户名单,王二 之后是张三,张三之后是李四,李四之后是赵 |六……如果要把新加入的王五安排在李四和赵 六之间,很简单,只要修改一下这个链表,把 李四后面的指针指向王五,把王五后面的指针 指向赵六即可。这样一来,插入一个新的数据 就是一件很容易的事了。
   ii. 弊端：查找不便
   如果我们要找出列表中第五个造访的客户是谁,因为没有 编号一说,因此必须要从头数一遍,一直数到 第五个。如果一个列表有几百万个记录单元, 数一遍可是很花时间的事情。

3.1 二叉树

1. 二叉树:
   在计算机中数值的相对大小，优于绝对大小。在计算机 中,由于经常要做的事情是判断真假、比较大 小、排序、挑选最大值这类的操作，专门设计一种数据结构,这种数据结 构被称为二叉树。
   
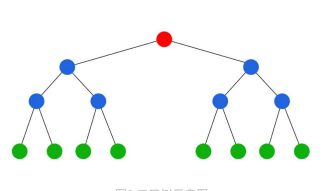
   a. 根:二叉树的根就是 图中顶上红色的那个点。
   b. 分叉:只能有两个分叉,在数学上, 两个分支和N个分支是等价的,或者说N个分 支的情况可以通过两个分支来实现。

2. 作用
   a. 排序：基础是a>b,b>c 那么c>a
   两条规则:
   第一,先来的占据根部,以及靠近顶部层 级比较高的位置,后来的放在相对靠下的位| 置。
   第二,每当一个分支的根部被占据之后, 接下来的数字,是和根部的数字进行比较,小 的放到左边分叉中,大的放到右边分叉中。
   这样安排得出来的二叉树,里面的数字从 左到右自然是从小到大排好序的。第一名,这种算法的 复杂度只有N,不是N乘以LogN。如果还需 要选出第二名,则额外增加Log N次计算就可 以了.
   
   b. 快速查找到某一个数值
   i. 查找最值：锦标赛排序法
   量级是N乘以Log N,和快 |速排序差不多。那么为什么不直接使用快速排 序？这种方 法在从N个选手中选出K个选手的事情中特别快。田径比赛中的算法问题.

   c. 遍历算法。
   i. 于网站的目录结构也是树状的 （当然它们有N个分叉）,因此,针对二叉树 的各种算法,稍加改变,就可以用于互联网。 比如,我们找到一个网站后,要下载一个网站 里面所有的网页,就会用到二叉树中的一种遍 历算法。
   3.思维

工程思维

直觉

生活环境将我们 的理解力限制在了生活空间给我们带来的直觉上。人直觉和生活常识非 常有用,但是有时缺乏知识的直觉会欺骗我们。比如：
很多人都在想人工智 能是否是万能的,人工智能 是人赋予机器的,他马上会问,这么聪 明的计算机难道不会自己进化出主动意 识么?
人想象不出体积这东西随着边长或 者直径增加时,会增长得有多么快：一个球直径大一倍,体积可是大7倍,而 不是想象中的两三倍。只有刮掉苹果里面直径的 80%，里外的重量才大致相当。
光速是个常数,产生不了叠加 的效果。

工程思维

是什么？与直觉思维不同，工程思维是数学或者工程工具去寻找答案，解决问题的一种思维方式。

有什么用？能够看清问题的本质，比如极限。

1. 在对数量的预估上不会有量级上的差别。
   Google-面试题：当前房间里能装下多少高尔夫球？这道题 目怎么入手呢?高尔夫球大 约直径4厘米,如果我们把它们整整齐齐 地像立方体那样码在一起,用眼睛估摸 |着房间的面积和高度,用小学数学就能 解决。 比如一个面积15平米,高3米的小会 议室,大约可以装70万个。

   为什么工程思维能够看清问题？

   工程思维是建立在数学、物理基础上，推翻物理学上的极限是近乎不可能的 事情,至少到今天为止还没有发生,因 为这样要颠覆整个物理学大厦。除了物 理学的极限,还有一个数学上的极限, 推翻它则是完全不可能的,因为数学是 严格建立在逻辑之上的,不是根据实验 观察得到的。比如：
   永动机。在历史上很多人试图制造出 热能转换效率大于一的热机(比如蒸汽 机或者内燃机）,甚至是永动机,因为 在他们看来只要不断提升效率,最终就 能不断获得突破。卡诺通过设计一个理想的热机，热机转化的效率，打破了永动机

怎么做？遵循工程思路解决问题。

1.用一个正确的数学或者工程工具去寻找答案，不会犯本质的错误。这就如同你看蚂蚁的爬行轨迹时, 不能跟在它的后面,而要从它的上方 |看。所谓掌握工程思维的技巧,就是要 比生活超越一个层级。

2.在没有数据之前不要轻易给出结论
1+1/2+1/4＋1/8＋ 1/16.……,不断加下去会是无穷大吗?有 人觉得会,因为加的数字是无穷无尽 的。其实,在数学上可以严格地证明即 便无限加下去,总和也不会超过2。1+1/2+1/3+1/4 + 1/5……,不断加下去会有极限么?如果 你按照上一个问题的思路来考虑这个问 题,得到的结论应该是有一个极限,因 为也是越加越小,加的数字趋近于零。 如果你是这么想的,我不得不告诉你, 非常遗憾,你猜错了,这个序列加下去 |还真是无穷大。

3.极限思维：极限对工程师来讲是一个非常重要的 概念。今天,稍微有一点经验的工程师 都知道,任何产品的性能都有一个物理 上无法突破的极限,这个极限并不需要 等到工程上接近它的那一天到来时才知 道,而是早就可以通过已有的理论直接 给出。

工程师

使学会了计算机编程,如果 还是按照人固有的思维定式理解计算机 问题,很快也会遇到天花板

IT从业人员遇到职业天花板的 第一个原因是一开始思维方式就错了。 像上面那位程序员,再努力写代码,恐 |怕几年后还是一个低水平的程序员。不 克服我们先天认识上的局限性,就无法 领会 IT 这个行业的精髓,当然事业也就 做不上去。

我对那个程序员讲,人生活在小数字 世界里,难免保留固有的习惯,但是既 然从事了计算机这个行业,就需要按照 计算机这个行业的规矩办事,不能先验 地假设数值一定不多。万一多了,笨办法增加的计算量可不止十倍、百倍,恐 怕是千倍,甚至一万倍。不换这个思 |路,永远成为不了合格的电脑工程师

在计算机这个世界里,几乎任 何常见的问题都已经有了优化过的答 案,作为从业者,首先要擅长使用专业 |人士给出的,验证了无数次的答案,而 |不是自己凭着生活经验拍脑袋想出一个 做法。

索引

@20180313第062封信 Google如何在一毫秒内找到你想要的上百万份文档？(OCR)

在处 理非常大量的数据时，使用顺序 查找,和二分查找，会力不从心。尤其使用后者需要对所有的 数据先排序。那么计算机对这个问题会建立索引。

排序查找

	在 Word中是不会对每一个词建索引的,因 此查找时是顺序查找,一个个来,查找 完一遍,计算机实际上是把你输入的文 章也浏览了一遍。在网页搜索中,因为 这个数据量实在太大,全世界大约有 1000亿个有意义的网页,即使每个网页 平均只有500个词,也是50万亿个词,是 不可能用顺序搜索的。在使用Word写作 时,一篇文章最多不过几万字,顺序浏 览一遍还是可以忍受的。
	
索引查找

	大数据时代，善于建索引,不仅是Google搜索 引擎查找信息非常快的根本原因,也是 保证Google的产品在信息爆炸时代能体现出高质量的原因。事实上在Google内 ,使用索引几乎成了所有软件开发的标准。今天一些公司做出来的软件产品质 |量不高,一个很重要的原因是开发者对 索引的重要性缺乏认识,思路还停留在 小数据时代,以至于很多功能的速度奇 慢无比

索引本身就是对信息进行等价的编码，编码后的信息被压缩，更有利于机器的识别。计算机 需要对里面的一切东西进行编号,因为 没有编号,就无从建立索引。

建索引比直接进到数据库中查找的好 处：

1.不需要进行排序,也可以快速查找到所 需要的信息。

		Google建立了全面、全球的索引。
		
			把在网络上所有能找 到的文档(以及图片、视频等等内容) 下载以后,会对每一个词建立索引,记 录下来每一个词都出现在哪一篇文档 （网页）中的哪一些具体的位置。比 |如"得到"这个词出现在第105个网页的第 4、9、37个位置,第403个网页的第9、 40、77个位置,第588个网页的第73、 203个位置,等等。,当一个互联网 的用户搜索"得到"这个词的时候,只要在 索引中找到这个词,就能通过一个操 作,把互联网上所有的包含"得到"的文本找出来了。
			
			Google在建 索引时,是对所有的词建索引的,而不 仅仅是对于一些重要的词建立索引。因 此,Google搜索出来的结果非常全,不 会漏掉很多。而大部分其他的搜索引擎,为了节省成本,常常把一些他们认 为不重要的词忽略掉,因此用户会发现 找到的网页没有Google找到的多
			
			此外,Google是对所有语言,所有 文字建一个统一的索引,而国内的搜索 引擎,会把文本分为中文的,英文的, 或者其他什么文字的,单独建立索引。 这在仅仅做一个市场生意时,起步可能 会工作量小一点,运营成本会高点,但 是,要想做全球化的生意,就几乎不可 能了。不仅如此,你如果在国内用这些 搜索引擎查找外文的东西,几乎找不 到。
			
			

2.由于不需要对数据库进行排序,当 数据库不断变动时,维护数据库的成本 就非常低。

3.每当遇到新的需求,就 建立新的索引好了。
	要找到在某 个单位工作的人,从某个大学毕业的 人,都很容易解决,因为再按照工作单 位建一个索引,按照毕业的学校建一个 索引就可以了。
4.将一些复杂的操作，切割简化。
	你要搜索一组关键词时,比 |如搜索同时包含,"得到"方法论"这两个 词,如果没有索引,可就麻烦了,即使 找到了包含"得到"这个词的网页,还要想 办法看看里面是否有"方法论"这个词,这 非常花时间。如果有了索引,我们知 道"得到"这个词出现在第105、403、588 等网页中,类似地,我们还知道"方法 论"这个词出现在403、545、1032等网 |页中,那么只要找到这两个索引的交 集,也就是403等等,就可以了,这个操|作就简单很多。如果你要搜索一个长句子,搜索引擎 会先把它分割成一个个独立的词,然后 根据每一个词的索引,找到这个句子。

随机化

第064封信l计算机科学中 的随机化一一比特币的基础

人是确定性的动物，但是在计算机科学中,很多时候 我们故意要把确定的东西变成随机的。这种思维应用在，查找和搜索中,另外,无处不在的信息加 密,也离不开随机化。比如说比特币也是靠随机化来做安全保 障。

起点——索引的不足：对于规模大的数据库,建立全面的索引，即使使用二分法进行查找也是非常耗时的。

假定北京市人名索引中有800万个不同的人名,或者Google的词表中有 800万个单词,通过二分查找需要23次可以找到"李强",或者"得到",也就是 log(800万)。对于查户籍这件事,23次查找真 算不上什么,但是对于语音识别或者机 器翻译,识别或者翻译一句话要查找上 万次词语,如果每一个词都要先在索引 中查23次才能找到,就是一个大负担 了。

逐步实现节省十倍时间的方法：笨办法是好办法的基础。

方法1,建立一个全面的索引，将23次变成1次：

汉字大约有两万多个,我 们就放大一下,假设是3万个吧!假如"李"这个字对应3500,"强"这个 字对应4003,那么"李强"就对应一个数 字组3500和4003。注意这个对应是唯一 的,没有歧义性。 接下来,我们做一个简单的数学变 换,把上面两个数字变成一个:30000*3500+4003=105,004,003, 也就是说拿105,004003这个数字作为"李 强"这个名字的编号。直 接 把"李强"存 放 到第 105,004,003个存储单元。只要用上面的公式做一次计算, 就能直接找到"李强"。

上述的索引带来的问题：上述是全面的编码，根据哈夫曼编码原理，上述的编码方式存在问题：

1.浪费内存，编码对应的是内存资源，将大量的内存分给了出现概率低，甚至为0的对象。

	不会有人起名 为"猪狗"或者类似的名字,于是对应数字 所占据的单元就被浪费掉了。大约会浪费多少呢?如果汉字是3万个,每个人都 是两字的名字,一共有9亿个不同的编号。假如北京市不重复的人名是800 万,大约浪费了99%上的编号(以及对 应的内存单元)。这显然不是一个好方法。

2.增长过快
	
	上述编码的基础是在3000的N次方，当大家起了三 字名,甚至四字名后,名字对应的编号 就可能非常大,以至于超出计算机的存储范围。

方法2.只保留编号的尾数，并且保证唯一。

我们注意到无论是"李强"的编号,还 是得到"的编号,都特别长,这么长的编 号是不太会重复的,那么稍微短一点行 不行?比如我们不管编号有多少位,只 保留最后的7位数字,也就是说将编号的 范围从9亿缩小到1000万。由于北京市只 有800万不同的人名,照理说准备1000 万个代号是够用的。

方法2的弊端，编码之所以不够用是因为两个不同的人名计算出的编号,尾数 可能恰巧重复,这种情况并不少见。解决这个问题,就是在尾号出现相同情况时,想 办法找一个没有那个词或者名字对应的 尾号,作为备选方案。我们既然有1000 万个代号,只有800万个名字,这个备选 的号码,一定是能够找到的。

保证唯一性的原理，找到最近的空编号。

		我们不 妨看这样一个例子。假如火车站买票时 是随机安排座位的,到了火车上,一定 有一些人拿到相同的座号。但是,如果 火车能载1000人,只卖了800张票,一定有办法安排每一个人就座的。具体的 做法是,先来的先坐下,如果后来的发 现自己票上的座位已经被占据了,那么 没关系,找最近的坐下即可。如果火车 上真有20??空座位,大家其实都能在附 近找到一个空座。在计算机中,安排这 种相同尾数的编号的方法和火车上安排 座位的原理是一样的。

方法3.随机指定一个名字或者词语的编号。方法一和方法二中,其实是按 照一个公式,编码取它的尾数。 这时,两个不同的名字有可能得到相同 的编号尾数。后来计算机科学家们发 现,如果随机地给每个名字,或者词语 进行编号,重复的可能性最小。于是, 计算机科学又有了一个小分支,如何产生伪随机数。

伪随机数，既然可编码信息就可以作为加密方式。

	因为它们并 非真的随机,只是看上去非常像随机产 生的。如何产生暂且不提。当伪随机数足够长时，除了编码者，别人是无法通过这个数字还原出原来的信息的,于是, 这个方法就能用来进行数据加密。
	
	进一步对编码的方式进行保护：
	
		当然,编码还需要解码，如果加密的 人和接收到信息后解密的人不是一个人,解密的一方需要知道加密的方法。如何能保证在解码的同时保证加密方式不泄露。如果这个方法给了对方,万一泄露出 去,就麻烦了。后来,数学家们想出了 一个不让对方知道自己怎么加密,却能够对某个信息解密的方法。这种方法在 密码学上被称为公开密钥,今天大部分加密算法都采用这种技术。
		
			比特币。
			
				比特币产生的算法类似印钞机,外面的人是不知道的,即使挖币的 矿工也不知道,否则你自己就能制造比特币了。产生比特币的过程要产生 一个比特币对应的随机数,也被称为私 钥(不公开的）,谁拿到它,就拥有了 比特币。这个随机数不能丢,否则比特币就不是你的了。
			
				验证比特币的真假。比 特币的公开密钥,则相当于验钞机,你 可以拿它验证比特币的真伪。如果验证 完了确认为真,你收了那个比特币,私 钥就归你了,当然,比特币的所有权和 使用权也就给了你了

自动化

Google所信奉的哲学是,相信机器 ,相信算法,相信自动化做事最终可以 比人工做得好

谷歌给网页建索引是由电脑自动完成。
Google建索引是对所有词建 立索引,包括看上去没有用的"的、地、 得","着、了、过"。在早期,只有 Google这样做,今
如果在 文化上留出了让人参与的缺口,以后遇 到技术难题就不可避免地要回避,这样 就难以进步了。此,Google一般不留 这样人工修补的口子,而是一条道走到 黑。如果技术不够好,有漏洞,就开发 更好的技术,弥补技术本身的不足,而 不是让人来弥补不足。
Google无人驾驶汽车,从0走到99只 花了六年时间,即2004~2010年。但是 从99%到99.99又花了6年时间,即 到2016年。如果让人完成最后1效率 一定更高,但这不是它的文化。

排序算法

人的产出是很难提高的，但是所做的事情是可以减少的，所以提高效率的方式根本方式是少做事，算法也是类似。

计算机的归并排序（快速），比冒泡排序和插入排序（传统）0更加高效的根本原因它少做了很多并不需要做的比较。对n个数进行排序：

传统排序的比较的次数为n的阶乘，大致为n*n：每次找出其中最大的。归并排序次数，比较次数：nlog(n)。

快速排序的原理
是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤如下：
1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2.设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3.比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4.重复步骤3直到某一指针超出序列尾；
5.将另一序列剩下的所有元素直接复制到合并序列尾。