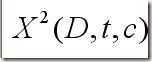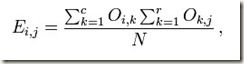寻根究底,探讨 chi -square特征词选择方法后面的数学支持
最近研究特征词选择算法,主要在研究chi方统计量的方法。
Christopher D Manning的书《信息检索导论》中(王斌译作191页,英文原版255页)的公式定义如下:
我所迷惑不解的是这个公式为啥长成这个样子?
对于![]() 我还是略有了解的,比如X~n(0,1),那么X^2就服从chi-square, 独立 独立的chi方分布相加后仍然是chi squared 变量,并且自由度为各个加数自由度的和。我遍搜了脑子里所有和chi-squared 分布有关的知识,还是推导不出这个公式。觉得这个公式怪怪的。如果说:
我还是略有了解的,比如X~n(0,1),那么X^2就服从chi-square, 独立 独立的chi方分布相加后仍然是chi squared 变量,并且自由度为各个加数自由度的和。我遍搜了脑子里所有和chi-squared 分布有关的知识,还是推导不出这个公式。觉得这个公式怪怪的。如果说:![]() 是服从N(0,,1),那么
是服从N(0,,1),那么
那么
查了manning书后面的关于数理统计的参考文献还是没有结果,而且目前我能找到的最原始论文Yiming Yang 1999那篇论文中也没有做过多的解释。最后根据Yiming Yang 论文中的一个词contigency table 终于找到了蛛丝马迹。以下列出资料来源:
http://en.wikipedia.org/wiki/Noncentral_chi-square_distribution
http://courses.washington.edu/urbdp520/UDP520/ChiSquareNotes.doc
http://en.wikipedia.org/wiki/Pearson's_chi-square_test
http://en.wikipedia.org/wiki/Contingency_table
最核心的理论可以说是 Pearson chi-square test. 这个检验主要应用于两个领域:
1。检测分布的拟合。也就是评价。根据抽样样本进行拟合后的分布与某个理论上的分布之间的差异性。2。检测两个随机变量(这两个随机变量的出现情况用contigency table 表示)是否独立。(这里的应用是属于第二种场合)
Pearson chi-square test的问题一般会出现两个表。一个是实际事件![]() 的contigency table,一个是期望事件
的contigency table,一个是期望事件![]() 的contigency table.
的contigency table.
注:contingency table可以这样理解:比如说有两个事件E1,E2。1事件有三个属性a1,a2,a3,E2事件有两个属性b1,b2,那么contigency table可以看成统计两个事件属性共现次数的矩阵。上面的例子就是3*2型的矩阵。
主要有两个步骤构成。一个是构造test statistic,一个是计算自由度。
根据 pearson chi-square test理论:
test statistic 的定义如下
The chi-square statistic is calculated by finding the difference between each observed and theoretical frequency for each possible outcome, squaring them, dividing each by the theoretical frequency, and taking the sum of the results.
也就是说
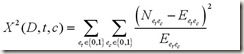 本身就是一个chi-squared 类型的test variable,那么它的freedom degree又该如何计算呢,
本身就是一个chi-squared 类型的test variable,那么它的freedom degree又该如何计算呢,
Pearson指出:
freedom degree 由 contingency table 的(row-1)*(column-1)定义。因为用于特征词选择算法的chi-square test的contingency table 维度为2*2所以自由度为1。
我们可以看下面的例子(来源:http://courses.washington.edu/urbdp520/UDP520/ChiSquareNotes.doc):下面例子用Chi-Square 检测地方医院的条件设施和社区人口的增减是否独立。 因为Contigency talbe 是3*2的,所以最后的自由度为2*1=2。
Contingency Test, or Chi-Square Test
Used to determine if there is association between nominal and ordinal scaled variables.
Our first test of association!
Based on two principles:
Marginal probability: MPr[x]: the probability of a single event happening
MPr[x] = # of times event happened
# of opportunities for event
Joint probability: JPr[x,y]: the probability of seeing two independent events happening at the same time.
JPr[x,y] = MPr[x] * MPr[y]
The logic of the chi-square test is to compare a set of actual conditions or data to an expected set of data that we would expect to see by chance.
We do this by creating cross-tab tables, which are simply descriptive tables of our actual and expected values.
We then plug our results into the chi-square calculation, and compare our results to the chi-square distribution, as with the other tests we’ve covered.
Example: Is the condition of local hospitals determined by the growth or decline in community population?
Independent variable? growth/decline of population
Dependent variable? Condition of hospital
Growth/declineàHospital condition
Actual data:
| Hospital Condition |
Community Pop. Increase 1980-2000 |
Community Pop. Decrease 1980-2000 |
Total |
Marginal Probability of a condition |
| Need of Major Repair |
10 |
50 |
60 |
MPr[MR]=60/200=.3 |
| Need of Minor Repair |
10 |
30 |
40 |
MPr[MiR]=40/200=.2 |
| Adequate Facilities |
80 |
20 |
100 |
MPr[A]=100/200=.5 |
| Total
|
100 |
100 |
200 |
|
| Marginal Probability of community |
MPr[PI]=100/200=.5 |
MPr[PD]=100/200=.5 |
Expected Table, if community growth does NOT affect hospital condition:
| Hospital Condition |
Community Pop. Increase 1980-2000 |
Community Pop. Decrease 1980-2000 |
Total |
| Need of Major Repair |
30 = JPr[MR,PI] = MPr[MR]*MPr[PI] = .3 * .5=.15(200 hospitals)= 30 |
30 = JPr[MR,PD] MPr[MR]*MPr[PD] .3 * .5=.15(200 hospitals)= 30 |
60 |
| Need of Minor Repair |
20 |
20 MPr[MiR]*MPr[PD] .2 * .5=.10(200 hospitals)=20 |
40 |
| Adequate Facilities |
50 |
50 MPr[A]*MPr[PD] .5 * .5=.25(200 hospitals)=50 |
100 |
| Total
|
100 |
100 |
200 |
Assumptions: Expected table is a representative sample. And community characteristics has no relationship to hospital condition.
Testable Hypotheses:
Ho: Aith row jth column = Eij (actual = expected, and thus independent does not affect dependent)
Ha: Aij ≠ Eij
Calculate test statistic:
 = (50-30)/30 + (10-30)/30 + (30-20)/20 + … ≈ 73
= (50-30)/30 + (10-30)/30 + (30-20)/20 + … ≈ 73
Determine rejection region:
d.f. = (# rows-1)(# columns-1) in this case (3-1)(2-1) = 2…
One tail, positive, always, due to squaring in test statistic
For alpha=.10
Ho is thus rejected, independent variable (growth of community) does not affect the dependent variable (condition of hospital).
Notes:
Don’t want to use chi-squared for small expected table values, so do cross tab test:
Cross tab test: Cannot have more than 20% of expected cells with values ≤ 5, and no cells can have value ≤ 3.
If it fails the test, you can do three things:
- Go to original cross tab table and combine rows or columns
- Eliminate a column or row (bad news, losing that data)
- Increase your sample size
Generally, Chi-square is for nominal data only. BUT it gets used inappropriately all the time. There is a loss of raw data going from ratio to ordinal.
Also note that chi-squared is a weak tool. It’s common because it’s one of the few tools to examine nominal/ordinal data. But it only tells you if an effect exists. It does not tell you the amount or direction of the effect.
注: manning书中的另一个公式:
和Yiming Yang 1999年的论文 A comparative Study on Feature Selection In Text Categorization 中 卡方公式是一个意思,这个公式可以通过前面的公式王斌译作191页,英文原版255页 经过很普通代换,提取公因式等操作推导出来
至此,理解完毕。