傅里叶变换推导

DR_CAN傅里叶变换系列视频笔记
直接进行推导可能太生硬，可以先看Heinrich的文章加以理解
本文仅作为笔记

part1: 三角函数的正交性

三角函数系
$$\{0,1,\sin x,\cos x,\sin 2x,\cos 2x,\cdots ,\sin nx,\cos nx,...\}$$

其中，$0=\sin 0x$，$1=\cos 0x$，$n=0,1,2\cdots$

正交：
什么是正交？
2维情况：

$$\begin{array}{l}a\cdot b=|a||b|\cos \phi =|a||b|\cos \frac{\pi }{2}=0\\ a\cdot b=(2,1)\cdot (-1,2)=2\times (-1)+1\times 2=0\end{array}$$
所以$a$和$b$正交

---

扩展到3维：
$$\begin{array}{l}a=(1,2,5)\\ b=(1,2,-1)\\ \\ a\cdot b=1\times 1+2\times 2-5\times 1=0\end{array}$$
$a$和$b$正交

---

扩展到任意维：

$$\begin{array}{rl}a& =\left(a_1,a_2,a_3,\dots a_n\right)\\ b& =\left(b_1,b_2,b_3,\cdots b_n\right)\\ & \\ a\cdot b& =a_1{b}_1+a_2{h}_2+\cdots a_n{b}_n\\ & =\sum _{j=1}^n{a}_i{b}_i=0\end{array}$$
$a$和$b$正交

---

扩展到函数：

$$\begin{array}{rl}a& =f(x)\\ b& =g(x)\\ & \\ a\cdot b& ={\int }_{x_0}^{x_1}f(x)g(x)dx=0\end{array}$$

$f(x)$和$g(x)$正交

---

所以提出在上面的三角函数系中任选2个，在$n\ne m$情况下是正交的：
$$\begin{array}{l}{\int }_{-\pi }^{\pi }\sin nx\cos mxdx=0n\ne m\\ \\ {\int }_{-\pi }^{\pi }\cos nx\cos mxdx=0n\ne m\\ \\ {\int }_{-\pi }^{\pi }\cos nx\sin mxdx=0n\ne m\\ \\ {\int }_{-\pi }^{\pi }\sin nx\sin mxdx=0n\ne m\\ \end{array}$$
现在证明正交性：
比如$n=0$，$m=1$
$${\int }_{-\pi }^{\pi }\cos 0x\sin 1xdx={\int }_{-\pi }^{\pi }\sin xdx=0$$

更一般的：
$m\ne n$
$$\begin{array}{rl}{\int }_{-\pi }^{\pi }\cos nx\cos mxdx& ={\int }_{-\pi }^{\pi }\frac{1}{2}[\cos (n-m)x+\cos (n+m)x]dx\\ & =\frac{1}{2}\left[{\int }_{-\pi }^{\pi }\cos (n-m)xdx+{\int }_{-\pi }^{\pi }\cos (n+m)xdx\right]\\ & =\frac{1}{2}\left[{\frac{1}{n-m}\sin (n-m)\lambda |}_{-\pi }^{\pi }+{\frac{1}{n+m}\sin (n+m)x|}_{-\pi }^{\pi }\right]\\ & =0\end{array}$$

---

$m=n$
$$\begin{array}{rl}{\int }_{-\pi }^{\pi }\cos mx\cos mxdx& ={\int }_{-\pi }^{\pi }\frac{1}{2}[1+\cos 2mx]dx\\ & =\frac{1}{2}\left[{\int }_{-\pi }^{\pi }1dx+{\int }_{-\pi }^{\pi }\cos 2mxdx\right]\\ & =\frac{1}{2}\left[{\int }_{-\pi }^{\pi }1dx+{\int }_{-\pi }^{\pi }\cos 0x\cos 2mxdx\right]\\ & =\frac{1}{2}{\int }_{-\pi }^{\pi }1dx\\ & =\pi \end{array}$$

小结：
理解三角函数正交性，什么是正交，证明三角函数正交

part2: 周期为$2\pi$的函数展开

周期$T=2\pi$的函数：
$$f(x)=f(x+2\pi )$$
图像:

像这样的函数可以转为一系列三角函数的加和：
$$\begin{array}{rl}f(x)& =\sum _{n=0}^{\infty }{a}_n\cos nx+\sum _{n=0}^{\infty }{b}_n\sin nx\end{array}\text{\hspace{1em}(2.1)}$$

式$(2.1)$可以把$a_0$提出来作为常数项：

$$\begin{array}{rl}f(x)& =a_0\cos 0x+\sum _{n=1}^{\infty }{a}_n\cos nx+b_0\sin 0x+\sum _{n=1}^{\infty }{b}_n\sin nx\\ & =a_0+\sum _{n=1}^{\infty }{a}_n\cos nx+\sum _{n=1}^{\infty }{b}_n\sin nx\end{array}\text{\hspace{1em}(2.2)}$$
至于为什么可以这样表示，可以看下面图片理解：

图片来自wikipedia

为什么是需要常数项$a_0$？
常数函数$g(x)=a_0$特性：

• 周期性
• 可以调节函数值/偏移

为什么是$\sin x,\cos x$？
$\sin x,\cos x$特性：

• 周期性
• 任何函数可以分解为偶函数和奇函数：$f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}$
  而$\sin x,\cos x$分别是奇函数和偶函数

为什么是$\sin nx,\cos nx$？

• n可以调节频率
• $\sin nx,\cos nx$的周期仍为$2\pi$

为什么$\sin nx,\cos nx$需要乘$a_n,b_n$？

• $\sin x,\cos x$的值域为-1到1，需要$a_n,b_n$调节幅值/振幅

配合Heinrich文章可以更好理解下图：

图片来自https://zhuanlan.zhihu.com/p/19763358
在这几幅图中，最前面黑色的线就是所有正弦波叠加而成的总和，也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来，而每一个波的振幅都是不同的。一定有细心的读者发现了，每两个正弦波之间都还有一条直线，那并不是分割线，而是振幅为0的正弦波！
来自https://zhuanlan.zhihu.com/p/19763358

还有些文章只用cos函数表示，但是考虑了相位
$$\begin{array}{rl}f(x)& =\sum _{n=0}^{\infty }{c}_n\cos (nx+\phi )\end{array}$$
但是实际上和式$(2.1)$是一样的，式$(2.1)$优点是不需要考虑相位

---

求$a_0$

在教科书中更常见的表达为：
$$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos nx+b_n\sin nx\right)\text{\hspace{1em}(2.3)}$$
为什么$a_0$变为了$\frac{a_0}{2}$？
原因可以在看完part4复数的表达形式后可以明白，这样做是为了表达统一。

转变过程：
其实这式$(2.2)$中$a_0$和式$(2.3)$中$a_0$虽然都为常数但是值不一样！
先求式$(2.2)$中$a_0$：

式$(2.2)$两边对$x$积分

$$\begin{array}{rl}{\int }_{-\pi }^{\pi }f(x)dx& ={\int }_{-\pi }^{\pi }{a}_{0}dx+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{a}_n\cos nxdx+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{b}_n\sin nxdx\\ & ={\int }_{-\pi }^{\pi }{a}_{0}dx+a_n{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }\cos 0x\cos nxdx+b_n{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }\cos 0x\sin nxdx\\ & =a_0{\int }_{-\pi }^{\pi }dx\\ & =2\pi a_0\end{array}$$
于是式$(1.2)$中$a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f(x)dx$

令$A_0=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)dx$，则$a_0=\frac{A_0}{2}$，所以有
$$\begin{array}{rl}f(x)& =a_0+\sum _{n=1}^{\infty }{a}_n\cos nx+\sum _{n=1}^{\infty }{b}_n\sin nx\\ & =\frac{A_0}{2}+\sum _{n=1}^{\infty }{a}_n\cos nx+\sum _{n=1}^{\infty }{b}_n\sin nx\end{array}$$
令$a_0=A_0$，此时便得到式$(1.3)$中的$a_0=A_0=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)dx$。

所以总结一下：
$$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos nx+b_n\sin nx\right)\text{\hspace{1em}(2.3)}$$
其中，$a_0=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)dx$

求$a_n$

两边乘$cosmx$，然后积分

$$\begin{array}{rl}{\int }_{-\pi }^{\pi }f(x)\cos mxdx& ={\int }_{-\pi }^{\pi }\frac{a_0}{2}\cos mxdx+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{a}_n\cos nx\cos mxdx+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{b}_n\sin nx\cos mxdx\\ & =0+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{a}_n\cos nx\cos mxdx+0\end{array}$$

上式中$n=m$或$n\ne m$:
$$\begin{array}{rl}& {\int }_{-\pi }^{\pi }\frac{a_0}{2}\cos mxdx=0\\ & {\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{b}_n\sin nx\cos mxdx=0\end{array}$$

$n\ne m$:
${\int }_{-\pi }^{\pi }{\sum }_{n=1}^{\infty }{a}_n\cos nx\cos mxdx=0$，于是无法求$a_n$，所以只能是$n=m$，此时：
累加只剩一项$n=m$
$$\begin{array}{rl}{\int }_{-\pi }^{\pi }f(x)\cos mxdx& ={\int }_{-\pi }^{\pi }f(x)\cos nxdx\\ & ={\int }_{-\pi }^{\pi }{a}_n\cos nx\cos nxdx\\ & =a_n{\int }_{-\pi }^{\pi }{\cos }^{2}xdx\\ & =a_n\pi \end{array}$$
于是有：
$$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos nxdx$$

求$b_n$

两边乘$sinmx$，然后积分

和求$a_n$同理可得：
$$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\sin nxdx$$

小结

周期$T=2\pi$函数：
$$f(x)=f(x+2\pi )$$

可以展开为：
$$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos nx+b_n\sin nx\right)\text{\hspace{1em}(2.3)}$$

其中，$$\begin{array}{rl}{a}_0& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)dx\\ a_n& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos nxdx\\ b_n& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\sin nxdx\end{array}$$
那么周期为$T=2\pi$可以如此展开，那么任意周期$T=2L$如何表示？

part3: 周期为2L的函数展开

周期为2L的函数展开

周期$T=2L$函数：
$$f(t)=f(t+2L)$$

图像：

换元：令$x=\frac{\pi }{L}t$，则$t=\frac{L}{\pi }x$

t	x
0	0
2L	2$\pi$
4L	4$\pi$

所以：
$$f(t)=f\left(\frac{L}{\pi }x\right)\triangleq g(x)$$

经过换元，则有：
$$g(t)=g(t+2\pi )$$
其中，$T=2\pi$
图像：

带入式$(2.3)$，有：
$$g(x)=\frac{a_0}{2}+\sum _{n=1}^n\left(a_n\cos nx+b_n\sin nx\right)$$

其中，
$$\begin{array}{rl}{a}_0& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }g(x)dx\\ a_n& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }g(x)\cos nxdx\\ b_n& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }g(x)\sin nxdx\end{array}$$

---

$x$与$t$的关系：
$$\begin{array}{rl}& x=\frac{\pi }{2}t\\ & \cos nx=\cos \frac{n\pi }{L}t\\ & \sin nx=\sin \frac{n\pi }{L}t\\ & g(x)=f(t)\end{array}$$

以及

$$\begin{array}{rl}{\int }_{-\pi }^{\pi }dx& ={\int }_{-L}^{L}d\frac{\pi }{L}t\\ \frac{1}{\pi }{\int }_{-\pi }^{\pi }dx& =\frac{1}{\pi }\frac{\pi }{2}{\int }_{-l}^{L}dt\\ & =\frac{1}{L}{\int }_{-L}^{L}dt\end{array}$$
把$x$替换为$t$：
$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos \frac{n\pi }{L}t+b_n\sin \frac{n\pi }{L}t\right)\text{\hspace{1em}(3.1)}$$
其中，
$$\begin{array}{rl}{a}_0& =\frac{1}{L}{\int }_{-L}^{L}f(t)dt\\ a_n& =\frac{1}{L}{\int }_{-L}^{L}f(t)\cos \frac{n\pi }{L}tdt\\ b_n& =\frac{1}{L}{\int }_{-L}^{L}f(t)\sin \frac{n\pi }{L}tdt\end{array}$$

---

工程中

$t$从0开始，周期为$T=2L$，角速度为$\omega =\frac{\pi }{L}=\frac{2\pi }{T}$
$${\int }_{-L}^{L}dt\to {\int }_0^{2L}dt\to {\int }_0^{T}dt$$
于是有：
$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos n\omega t+b_n\sin n\omega t\right)\text{\hspace{1em}(3.2)}$$
其中，
$$\begin{array}{rl}\omega & =\frac{\pi }{L}=\frac{2\pi }{T}\\ a_0& =\frac{2}{T}{\int }_0^{T}f(t)dt\\ a_n& =\frac{2}{T}{\int }_0^{T}f(t)\cos n\omega t\\ b_n& =\frac{2}{T}{\int }_0^{T}f(t)\sin n\omega t\end{array}$$

---

例子

下面用个例子来说明函数展开
周期$T=20$，角速度$\omega =\frac{2\pi }{T}=\frac{2\pi }{20}=\frac{1}{10}\pi$
函数图像：

求解过程(直接用DR_CAN老师的手写了，太多了。。)：

最终结果为：
$$f(t)=5+\sum _{n=1}^{\infty }\frac{8}{n\pi }\cdot \sin \frac{n\pi }{10}t$$
其中，$n=1,3.5,7\cdots$

发现：
$$\underset{n\to +\infty }{\lim }\frac{8}{n\pi }=0$$
也就是说$n$越大，对于正弦函数振幅越小，频率越大

或者在geogebra中画出：

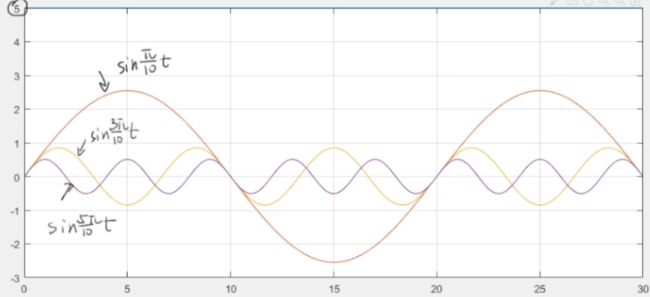
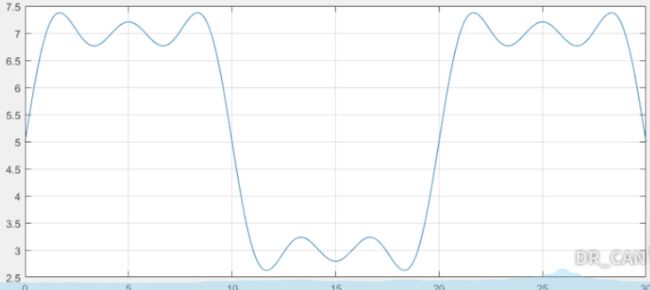
只要级数够多"弯的也能变直"

小结

周期$T=2L$函数：
$$f(t)=f(t+2L)$$

可以展开为：
$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos \frac{n\pi }{L}t+b_n\sin \frac{n\pi }{L}t\right)\text{\hspace{1em}(3.1)}$$
其中，
$$\begin{array}{rl}{a}_0& =\frac{1}{L}{\int }_{-L}^{L}f(t)dt\\ a_n& =\frac{1}{L}{\int }_{-L}^{L}f(t)\cos \frac{n\pi }{L}tdt\\ b_n& =\frac{1}{L}{\int }_{-L}^{L}f(t)\sin \frac{n\pi }{L}tdt\end{array}$$

---

或者表示为：
$$f(t)=f(t+T)$$

展开为：
$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos n\omega t+b_n\sin n\omega t\right)\text{\hspace{1em}(3.2)}$$

其中，
$$\begin{array}{rl}\omega & =\frac{\pi }{L}=\frac{2\pi }{T}\\ a_0& =\frac{2}{T}{\int }_0^{T}f(t)dt\\ a_n& =\frac{2}{T}{\int }_0^{T}f(t)\cos n\omega t\\ b_n& =\frac{2}{T}{\int }_0^{T}f(t)\sin n\omega t\end{array}$$

任意周期为$T=2L$可以如此展开，那么周期无限大时$T=\infty$如何表示？

part4: 傅里叶级数的复数形式

先回顾一下欧拉公式：
$$e^{i\theta }=\cos \theta +i\sin \theta$$
证明欧拉公式：

这部分也是来自DR_CAN的视频

设：
$$f(\theta )=\frac{e^{i\theta }}{\cos \theta +i\sin \theta }$$
对其求导：
$$\begin{array}{rl}{f}^{\prime }(\theta )& =\frac{i{e}^{i\theta }(\cos \theta +i\sin \theta )-e^{i\theta }(-\sin \theta +i\cos \theta )}{(\cos \theta +i\sin \theta {)}^2}\\ & =\frac{i{e}^{i\theta }\cos \theta -e^{i\theta }\sin \theta +e^{i\theta }\sin \theta -e^{i\theta }i\cos \theta }{(\cos \theta +i\sin \theta {)}^2}\\ & =0\end{array}$$

所以:$f^{\prime }(\theta )=0\Rightarrow f(\theta )$为常数
为了确定常数，可以令$\theta =0$，带入$f(0)=1$，所以：
$$\frac{e^{i\theta }}{\cos \theta +i\sin \theta }=1\Rightarrow e^{i\theta }=\cos \theta +i\sin \theta$$

---

除了需要了解欧拉公式外，还需要了解$\cos \theta ,\sin \theta$的复数表示

因为：
$$\begin{array}{rl}& e^{i\theta }=\cos \theta +i\sin \theta \\ & e^{-i\theta }=\cos \theta -i\sin \theta \end{array}$$
所以：
$$\begin{array}{rl}& \cos \theta =\frac{1}{2}\left(e^{i\theta }+e^{-i\theta }\right)\\ & \sin \theta =-\frac{1}{2}i\left(e^{i\theta }-e^{-i\theta }\right)\end{array}\text{\hspace{1em}(4.1)}$$

---

用式$(4.1)$带入式$(3.2)$中，于是有
$$\begin{array}{rl}f(t)& =\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[a_n\frac{1}{2}\left(e^{in\omega t}+e^{-in\omega t}\right)-\frac{1}{2}j{b}_n\left(e^{in\omega t}-e^{-in\omega t}\right)\right]\\ & =\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[\frac{a_n-i{b}_n}{2}{e}^{in\omega t}+\frac{a_n+i{b}_n}{2}{e}^{-in\omega t}\right]\\ & =\frac{a_0}{2}+\sum _{n=1}^{\infty }\frac{a_n-ibn}{2}{e}^{in\omega t}+\sum _{n=1}^{\infty }\frac{a_n+i{b}_n}{2}{e}^{-in\omega t}\\ & =\frac{a_0}{2}+\sum _{n=1}^{\infty }\frac{a_n-ibn}{2}{e}^{in\omega t}+\sum _{n=-\infty }^{-1}\frac{a_{-n}+i{b}_{-n}}{2}{e}^{inwt}\\ & =\sum _{n=0}^0\frac{a_0}{2}{e}^{in\omega t}+\sum _{n=1}^{\infty }\frac{a_n-ibn}{2}{e}^{in\omega t}+\sum _{n=-\infty }^{-1}\frac{a_{-n}+i{b}_{-n}}{2}{e}^{inwt}\\ & =\sum _{n=-\infty }^{\infty }{C}_n{e}^{inwt}\end{array}\text{\hspace{1em}(4.2)}$$
在式$(4.2)$第5步中，可以发现3个部分都有$e^{in\omega t}$，所以提出来并且系数用$Cn$表示。此外为什么累加可以合并，这里$n$是离散的，所以${\sum }_{n=-\infty }^{-1},{\sum }_{n=0}^0,{\sum }_{n=1}^{\infty }$累加区间合并就是${\sum }_{-\infty }^{\infty }$。

现在分析$C_n$:
$$C_n=\{\begin{array}{ll}\frac{a_0}{2},& n=0\\ & \\ \frac{a_n-i{b}_n}{2},& n=1,2,3,4\cdots \\ & \\ \frac{a_{-n}+i{b}_{-n}}{2}& n=-1,-2,-3,-4\cdots \end{array}\text{\hspace{1em}(4.3)}$$
发现2、3行可以合并(DR_CAN先带入$a_n$和$b_n$再得出此结论，实际上一样的)：
$$C_n=\{\begin{array}{ll}\frac{a_0}{2},& n=0\\ & \\ \frac{a_n-i{b}_n}{2},& n\ne 0\end{array}$$
带入式$(3.2)$的条件：
$$\begin{array}{rl}{a}_0& =\frac{2}{T}{\int }_0^{T}f(t)dt\\ a_n& =\frac{2}{T}{\int }_0^{T}f(t)\cos n\omega t\\ b_n& =\frac{2}{T}{\int }_0^{T}f(t)\sin n\omega t\end{array}$$
于是：
$$C_n=\{\begin{array}{ll}\frac{1}{T}{\int }_0^{T}f(t)dt,& n=0\\ & \\ \frac{1}{T}{\int }_0^{T}f(t)e^{-in\omega t}dt,& n\ne 0\end{array}$$
由于，$e^{-i0\omega t}=1$，所以最终：
$$C_n=\frac{1}{T}{\int }_0^{T}f(t)e^{-in\omega t}dt$$

小结

式$(4.2)$也就变为：
$$\begin{array}{rl}f(t)& =\sum _{n=-\infty }^{\infty }{C}_n{e}^{in\omega t}\end{array}\text{\hspace{1em}(4.4)}$$

其中，
$$\begin{array}{r}{C}_n=\frac{1}{T}{\int }_0^{T}f(t)e^{-in\omega t}dt\end{array}$$

这也就是傅里叶级数的复数形式。
此外，也可以看到式$(4.3)$中n=0时$C_n=\frac{a_0}{2}$，正是因为式$(2.3)$中$a_0$转变为$\frac{a_0}{2}$，复数表达形式可以如此简洁。

part5:从傅里叶级数推导傅里叶变换

在式$(4.4)$中，$\omega =\frac{2\pi }{T}$称为基频率，发现一个$n\omega$对应一个$C_n$

$C_n$是一个复数，取$|C_n|$表示幅度，间隔：
$$\Delta \omega =(n+1)w-nw=w=\frac{2\pi }{T}\text{\hspace{1em}(5.1)}$$

其在频域图像中表示(纵轴表示幅度$|C_n|$，横轴表示频率$n\omega$)：

图片来自https://zhuanlan.zhihu.com/p/19763358

在part3提出周期无限大时$T=\infty$如何对函数展开？

实际上：
$$\underset{T\to \infty }{\lim }{f}_T(t)=f(t)$$
也就是$T\to \infty$周期函数将不再是周期函数。

间隔：
$$\underset{T\to \infty }{\lim }\Delta \omega =\underset{T\to \infty }{\lim }\frac{2\pi }{T}=0$$
所以$T\to \infty$频域图像上离散的点将变为连续。

连续长这样：

图片来自https://zhuanlan.zhihu.com/p/19763358

---

式$(5.2)$可知$\frac{1}{T}=\frac{\Delta \omega }{2\pi }=\frac{\omega }{2\pi }$

式$(4.4)$也可以表示为：
$$\begin{array}{rl}f(t)& =\sum _{n=-\infty }^{\infty }[\frac{1}{T}{\int }_0^{T}f(t)e^{-in\omega t}dt]e^{in\omega t}\\ & =\sum _{n=-\infty }^{\infty }[\frac{\Delta \omega }{2\pi }{\int }_0^{T}f(t)e^{-in\omega t}dt]e^{in\omega t}\\ & =\sum _{n=-\infty }^{\infty }[\frac{\omega }{2\pi }{\int }_0^{T}f(t)e^{-in\omega t}dt]e^{in\omega t}\end{array}\text{\hspace{1em}(5.2)}$$

在$T\to \infty$：
$$\begin{array}{rl}& {\int }_{-\frac{T}{2}}^{\frac{T}{2}}dt\to {\int }_{-\infty }^{+\infty }dt\\ & \sum _{n=-\infty }^{\infty }\omega \to {\int }_{-\infty }^{+\infty }\omega dn={\int }_{-\infty }^{+\infty }dn\omega \end{array}$$
令$\mu =\frac{n}{T}$，则$n\omega =n\frac{2\pi }{T}=2\pi \frac{n}{T}=2\pi \mu$，带入式$(5.2)$
$$\begin{array}{rl}f(t)& =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(t)e^{-i2\pi \mu t}dt{e}^{i2\pi \mu t}d\mu \end{array}\text{\hspace{1em}(5.3)}$$

令：
$$F(\mu )={\int }_{-\infty }^{+\infty }f(t)e^{-i2\pi \mu t}dt$$

这便是傅里叶变换(在数字图像处理中傅里叶变换公式就是上述公式，第3版p227)。

令：
$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }f(\mu )e^{i2\pi \mu t}d\mu$$

这便是傅里叶逆变换(在数字图像处理中傅里叶逆变换公式就是上述公式，第3版p227)。

小结

此外，更形象的理解傅里叶变换可以参考视频https://www.bilibili.com/video/BV1pW411J7s8

本人水平有限，仅作为笔记复习和参考，如有错误，欢迎指出。

参考

DR_CAN的傅里叶变换系列视频纯干货数学推导_傅里叶级数与傅里叶变换
傅里叶展开形式由来：引垂思汀的视频傅里叶级数、傅里叶变换与拉普拉斯变换
部分图片：Heinrich的文章傅里叶分析之掐死教程（完整版）更新于2014.06.06
还有：DBinary的文章傅里叶变换推导详解