算法导论期末详细归纳总结(含习题和完整算法代码)
-
2021新年似旧年,第一篇牛年博客!
-
4号算法导论期末考试,这篇文章助各大学子期末冲刺高分
-
给大家推荐一个超牛逼的算法动态图网址: https://visualgo.net/zh
一: 各种算法时间复杂度
(一) 排序算法:
- 直接插入排序: O( n 2 n^2 n2)、稳定
- shell排序: O( n 1.3 n^{1.3} n1.3)、不稳定
- 归并排序: O(n l g n lgn lgn)、稳定
- 堆排序: O(n l g n lgn lgn)、不稳定
- 快速排序: O(n l g n lgn lgn)、不稳定
- 基数排序: O(d( n + k n+k n+k))、稳定
- 平方阶有: 直接选择排序、冒泡排序、直接插入排序;线性阶的有桶排序、基数排序、计数排序;
- 稳定的有: 冒泡排序、归并排序、基数排序、直接插入排序
- 不稳定的有: 选择排序、快速排序、希尔排序、堆排序
(二) 各大算法实例
- 最大子数组:T(n) = θ( n l g n nlgn nlgn)
- 矩阵乘法的Strassen算法: T(n) = θ( n l g 7 n^{lg7} nlg7)
- 广度优先搜索: O \Omicron O( V + E V+E V+E)
- 最长特征序列的长度期望θ( l g n lgn lgn)
- 生日悖论: θ( n \sqrt n n)
二: 广度优先搜索( b f s bfs bfs)
- 大致思路: 从开始节点出发,遍历所有结点,通过队列这一数据结构实现入队出队操作,一直到找到最终结点时才执行回溯操作,最终路径列表里面的结点个数减去1则为最短路径!
- 代码如下,建议先看完大致思路再看代码,最好自己能够debug走一遍
from collections import deque
from collections import namedtuple
# start_node: 开始节点
# end_node: 目标节点
# graph: 图字典
def bfs(start_node, end_node, graph):
node = namedtuple('node', 'name, from_node') # 使用nametuple定义节点,用于存储前置节点
search_queue = deque() # 使用双端队列, 根据先进先出获取下一个遍历的节点
name_search = deque() # 存储队列中已有节点名称
visited = {
} # 存储已访问过的节点
search_queue.append(node(start_node, None)) #填入初始节点, 从队列后面加入
name_search.append(start_node) # 存储已访问过的节点
path = [] # 回溯路径
path_len = 0 # 路径长度
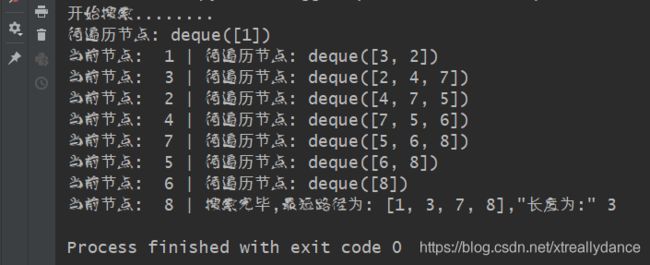
print('开始搜索........')
# 当搜索队列不为空则一直遍历下去
while search_queue:
print('待遍历节点:', name_search)
current_node = search_queue.popleft() # 从队列前边获取节点
name_search.popleft() # 将名称也相应弹出
if current_node.name not in visited: # 当前节点没有被访问过的话
print('当前节点: ', current_node.name, end=' | ')
if current_node.name == end_node: # 找到目标节点
pre_node = current_node # 路径回溯的关键在于每个节点中存储的前置节点
while True:
if pre_node.name == start_node: # 如果前置节点为当前节点
path.append(start_node) # 将当前节点加入路径,保证路径的完整性
break # 退出
else:
path.append(pre_node.name) # 不断将前置节点名称加入路径
pre_node = visited[pre_node.from_node] # 取出前置节点的前置节点
path_len = len(path) - 1
break
else:
visited[current_node.name] = current_node # 没找到则将该节点设置为已访问
for node_name in graph[current_node.name]: # 遍历相邻节点
if node_name not in name_search: # 如果相邻节点不在搜索队列中
search_queue.append(node(node_name, current_node.name))
name_search.append(node_name)
print(f'搜索完毕,最短路径为: {path[::-1]},"长度为:" {path_len}')
if __name__ == '__main__':
graph = dict() # 使用字典表示有向图
graph[1] = [3, 2]
graph[2] = [5]
graph[3] = [4, 7]
graph[4] = [6]
graph[5] = [6]
graph[6] = [8]
graph[7] = [8]
graph[8] = []
bfs(1, 8, graph)
三: 先序,中序,后序遍历结果
- 先序遍历: 根、左子树、右子树
- 中序遍历: 左子树、根、右子树
- 后序遍历: 左子树、右子树、根
1: 已知先序为ABCDEFGH、中序为BDCEAFHG, 求后序
- 首先根据先序和中序画出二叉树的图形
- 第一步通过先序找根节点: A, 再去中序中找到A的位置,A左边的序列BDCE为左子树,A右边的序列FHG为右子树
- 先从中序看左子树BDCE,先序中BDCE中最先出现的则为根结点,B结点最先出现,因此B结点左子树为空,右子树为DCE;在从先序中看C最先出现则为根结点,C左边的D为左子树,右边的E为右子树,画出如上图所示的左子树
- 再从中序看右子树FHG,先序中最先出现的是F,因此F为根节点,左子树为空,右子树为HG;先序中G比H先出现,所以G为根节点,H为G的左孩子,再画出右子树,整颗二叉树就画出来如上图所示啦!
- 最后根据如图所示的二叉树写出后序遍历序列,大致遍历思路如下:首先后序遍历是先访问左子树再访问右子树,最后访问根节点;所以从根节点A开始访问左子树,找到结点B,再访问B的左子树为空,接着再访问B的右子树,找到根节点C,再访问C的左子树,找到结点D,再访问D的左子树为空,访问D的右子树也为空,最后输出根节点D;然后再访问C的右子树E,E的左子树为空,右子树也为空,最后输出结点E;C的左子树访问完毕,右子树访问完毕,接着打印输出结点C;B的左子树访问完毕,右子树访问完毕,接着打印结点B,然后A的左子树访问完毕,开始访问A的右子树;先找到节点F,访问其左子树为空,再访问其右子树,找到结点G,访问其左子树,找到结点H,其左右孩子皆为空,因此打印输出H,然后访问结点G的右孩子即右子树为空,当左右孩子都访问完毕,打印输出结点G,接着F的右子树访问完毕,再打印结点F,A的右子树访问完毕,最后输出结点A,最终的后序遍历的序列为: DECBHGFA
如果已知中序和后序,大致思路与上述类似,只是后序中后出现的结点为根节点
四: 插入排序代码分析
def insert_sort(list):
for i in range(1, len(list): # i从第二个元素开始
temp = list[i] # 将要插入的值赋给temp
j = i - 1 # j为i位置后一个(如果i指向第二个,则j就是第一个)
# 如果j非负,且j对应的值大于temp
while(j>=0) & (list[j] > temp)
# ps: 这里和步骤需要自己动手画图更容易理解下面两行代码意思
# 大致意思是将元素进行后移,留下一个空位能被temp插入
list[j+1] = list[j]
j = j - 1
list[j+1] = temp # 将temp的值插入
- 下面是一个我录制的插入排序的动态图,建议反复食用,没有vip就有水印难受!
五: 归并排序代码分析
- 雅哈咖啡真的牛,睡意全无,贴张昨天看小库里比赛时的截图!!
# 归并排序python代码
def MergeSort(lists):
if len(lists) <= 1 : # 如果列表数组长度小于等于1,则返回其本身
return lists
middle = len(lists) // 2 # 找到其中间位置middle
# 采用分治思想,分为左边与右边两个子问题,然后再递归再分
left = MergeSort(lists[:middle])
right = MergeSort(lists[middle:])
return merge(left, right) # merge 合并左右俩列表
def merge(a, b):
c = [] # 用来接收a、b列表的值
h = j = 0 # 用于遍历a、b列表的下标
while j < len(a) and h < len(b):
if a[j] < b[j]:
# 如果a的值小于b的值
c.append(a[j])
j += 1
else:
# 添加b的值
c.append(b[h])
h += 1
if j == len(a): # 如果a的列表先遍历完了
for i in b[h:]:
c.append(i) # 则直接遍历添加b中的元素
else:
for j in a[j:]:
c.append(i) # 反之则直接遍历添加a中的元素
return c # 返回列表c
if __name__ == '__main__':
a = [5, 2, 4, 7, 1, 3, 2, 6]
b = [9, 8, 7, 6, 5, 4, 3, 2, 1]
A = [3, 41, 52, 26, 38, 57, 9, 49]
print(MergeSort(a))
print(MergeSort(b))
print(MergeSort(A))
'''
结果如下:
[1, 2, 2, 3, 4, 5, 6, 7]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[3, 9, 26, 38, 41, 49, 52, 57]
Process finished with exit code 0
'''
六: 堆排序代码分析
- 堆排序的核心思想无非就是: 先建堆,可以是极大堆也可以是极小堆,然后在排序的过程中维护堆的性质(根节点大于左孩子与右孩子或者根节点小于左孩子与右孩子),具体python代码如下所示:
# 堆排序
def heap_sort(array):
# 从完全二叉树最后一个非叶子结点开始
first = len(array) // 2 - 1
for start in range(first, -1, -1):
# 从下到上, 从右到左对每个非叶子结点进行调整,循环构建最大堆
big_heap(array, start, len(array) - 1)
for end in range(len(array) - 1, 0, -1):
print(array[0]) # 打印堆顶
# 交换数组中的堆顶和堆底
array[0], array[end] = array[end], array[0]
# 重新调整位完全二叉树,构造最大堆
big_heap(array, 0, end-1)
print('',end='')
print(array[0]
print('-------------------')
return array
def big_heap(array, start, end):
root = start
# 左孩子索引
child = root * 2 + 1
while child <= end:
# 节点有右子节点, 并且右节点的值大于左子节点, 则将child变为右子节点的索引
# 比较子节点中较大的节点
if child + 1 <= end and array[child] < array[child + 1]:
child += 1
if array[root] < array[child]:
# 交换节点与子节点中较大者的值
array[root], array[child] = array[child], array[root]
# 交换值后, 如果存在孙节点, 则将root设为子节点, 继续与子孙节点进行比较
root = child
child = root * 2 + 1
else:
break
if __name__ == '__main__':
array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]
a = heap_sort(array)
print(a)
'''
结果如下所示:
50
45
36
30
27
24
21
17
15
10
7
5
----------------------------
[5, 7, 10, 15, 17, 21, 24, 27, 30, 36, 45, 50]
'''
七: 快速排序代码分析
- 快速排序的核心思想是: 先选取一个主元,左侧的数值小于主元,右侧的数值大于该主元,主元可以任意选择(可以是最左侧的元素,亦或是最右侧的元素都可)
data = [1, 14, 20, 5, 8, 18, 14, 7, 3]
def quick_sort(data, start, end):
i = start
j = end
# i与j重合, 一次排序结束
if i >= j:
return
# 设置最左边的值为基准值
flag = data[start]
while i < j:
while i < j and data[j] >= flag: # 如果右边元素大于flag
j -= 1 # j向左移动一位
# 当右边找到小于flag的值, 则交换i、j对应元素的值
data[i] = data[j]
while i < j and data[i] <= flag: # 如果左边的元素小于flag
i += 1 # i向右移动一位
# 当左边找到小于flag的值, 则交换i、j对应元素的值
data[j] = data[i]
# 将主元的元素赋值给最后i所处位置对应的元素
data[i] = flag
# 除去i之外的两段递归
quick_sort(data, start, i-1)
quick_sort(data, i+1, end)
quick_sort(data, 0, len(data)-1)
print(data)
'''
最终结果如下所示:
[1, 3, 5, 7, 8, 14, 14, 18, 20]
Process finished with exit code 0
'''
八: 递归方程的求解: 代入法、主方法、递归树
九: 小题(选择填空)
(一): 选择题
1: 二分搜索算法是利用( A )实现的算法。
A、分治策略
B、动态规划法
C、贪心法
D、回溯法
2:下列不是动态规划算法基本步骤的是( A )。
A、找出最优解的性质
B、构造最优解
C、算出最优解
D、定义最优解
3:最长公共子序列算法利用的算法是( B )。
A、分支界限法
B、动态规划法
C、贪心法
D、回溯法
4:下列算法中通常以自底向上的方式求解最优解的是( B )。
A、备忘录法
B、动态规划法
C、贪心法
D、回溯法
5:衡量一个算法好坏的标准是(C )。
A 运行速度快
B 占用空间少
C 时间复杂度低
D 代码短
6: 以下不可以使用分治法求解的是(D )。
A 棋盘覆盖问题
B 选择问题
C 归并排序
D 0/1背包问题
7:一个问题可用动态规划算法或贪心算法求解的关键特征是问题的( B )。
A、重叠子问题
B、最优子结构性质
C、贪心选择性质
D、定义最优解
8:广度优先是( A )的一搜索方式。
A、分支界限法
B、动态规划法
C、贪心法
D、回溯法
8:背包问题的贪心算法所需的计算时间为( B )。
A、O(n2n)
B、O(nlogn)
C、O(2n)
D、O(n)
9: 实现棋盘覆盖算法利用的算法是( A )。
A、分治法
B、动态规划法
C、贪心法
D、回溯法
10:下面是贪心算法的基本要素的是( C )。
A、重叠子问题
B、构造最优解
C、贪心选择性质
D、定义最优解
11:贪心算法与动态规划算法的主要区别是( B )。
A、最优子结构
B、贪心选择性质
C、构造最优解
D、定义最优解
12:( D )是贪心算法与动态规划算法的共同点。
A、重叠子问题
B、构造最优解
C、贪心选择性质
D、最优子结构性质
13:矩阵连乘问题的算法可由(B)设计实现。
A、分支界限算法
B、动态规划算法
C、贪心算法
D、回溯算法
14: 0-1背包问题的回溯算法所需的计算时间为( A )
A、O( n 2 n^2 n2)
B、O(nlogn)
C、O(2n)
D、O(n)
15: 使用分治法求解不需要满足的条件是(A )。
A 子问题必须是一样的
B 子问题不能够重复
C 子问题的解可以合并
D 原问题和子问题使用相同的方法解
16: 下列是动态规划算法基本要素的是( D )。
A、定义最优解
B、构造最优解
C、算出最优解
D、子问题重叠性质
17: 回溯法的效率不依赖于下列哪些因素( D )
A.满足显约束的值的个数
B. 计算约束函数的时间
C. 计算限界函数的时间
D. 确定解空间的时间
18: 下面关于NP问题说法正确的是(B )
A NP问题都是不可能解决的问题
B P类问题包含在NP类问题中
C NP完全问题是P类问题的子集
D NP类问题包含在P类问题中
19: 分支限界法解旅行售货员问题时,活结点表的组织形式是( A )
A、最小堆
B、最大堆
C、栈
D、数组
20: Strassen矩阵乘法是利用( A )实现的算法。
A、分治策略
B、动态规划法
C、贪心法
D、回溯法
(二): 填空题
- 算法的复杂性有时间复杂性和空间复杂性之分
- 程序是算法用某种程序设计语言的具体实现
- 算法的“确定性”指的是组成算法的每条指令是清晰的,无歧义的
- 拉斯维加斯算法找到的解一定是正确解
- 算法是指解决问题的一种方法或一个过程
- 从分治法的一般设计模式可以看出,用它设计出的程序一般是递归算法
- 算法是由若干条指令组成的有穷序列,且要满足输入,输出、确定性和有限性四条性质
- 快速排序算法的性能取决于划分的对称性
- 动态规划算法的两个基本要素是:最优子结构性质和重叠子问题性质
- 快速排序算法是基于分治策略的一种排序算法
十: 钢条切割问题
(一): 钢条切割递归式如下所示(自顶向下递归实现)
def CUT_ROD(p,n):
if n == 0 :
return 0
q = float('-inf') # 表示负无穷
for i in range(1, n+1):
q = max(q, p[i] + CUT_ROD(p, n-i))
return q
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
print(CUT_ROD(p, 5))
'''
结果:
13
'''
T ( n ) = 1 + ∑ j = 0 n − 1 T ( j ) T(n) = 1 + \sum_{j=0}^{n-1}{T(j)} T(n)=1+j=0∑n−1T(j)
第一项"1"表示函数的第一次调用(递归调用树的根节点), T(j)位调用CUT-ROD(p,n-i)所产生的所有调用(包括递归调用)的次数,此处 j=n-i, T(n) = 2^n
(二) 自顶向下备忘录代码实现:
def MemorizeCutRoad(p, n):
r = [-1]*(n+1)
def MemorizeCutRoadAux(p, n, r):
if r[n] >= 0:
return r[n]
q = -1
if n == 0:
q = 0
else:
for i in range(1, n+1):
q = max(q, p[i] + MemorizeCutRoadAux(p, n-i,r))
r[n] = q
return q
return MemorizeCutRoadAux(p, n, r), r
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
print("最大收益为:", MemorizeCutRoad(p, 5))
'''
结果:
最大收益为: (13, [0, 1, 5, 8, 10, 13])
'''
- ps: 这里钢铁切割只是大致列了自顶向下的递归与备忘录两种情况,具体的钢铁切割详细可以细看这篇文章(关于自底向上的),注释详细!
https://blog.csdn.net/xtreallydance/article/details/111187442
十一: 矩阵连乘问题
- 求<5,10,3,12,5,50,6>的矩阵链的最优括号方案
- A 5 ∗ 10 A_{5*10} A5∗10( A 1 A_1 A1)、 A 10 ∗ 3 A_{10*3} A10∗3( A 2 A_2 A2)、 A 3 ∗ 12 A_{3*12} A3∗12( A 3 A_3 A3)、 A 12 ∗ 5 A_{12*5} A12∗5( A 4 A_4 A4)、 A 5 ∗ 50 A_{5*50} A5∗50( A 5 A_5 A5)、 A 50 ∗ 6 A_{50*6} A50∗6( A 6 A_6 A6)、
void matrixChain(){
for(int i=1;i<=n;i++)m[i][i]=0;
for(int r=2;r<=n;r++)//对角线循环
for(int i=1;i<=n-r+1;i++){
//行循环
int j = r+i-1;//列的控制
//找m[i][j]的最小值,先初始化一下,令k=i
m[i][j]=m[i][i]+m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
//k从i+1到j-1循环找m[i][j]的最小值
for(int k = i+1;k<j;k++){
int temp=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(temp<m[i][j]){
m[i][j]=temp;
//s[][]用来记录在子序列i-j段中,在k位置处断开能得到最优解
s[i][j]=k;
}
}
}
}


详细了解矩阵链乘法可以参考这篇博客https://www.cnblogs.com/crx234/p/5988453.html
十二: 最长公共子序列
- 核心思想: 查找A、B两个序列公共相同的最长子序列
- 例如a = ‘ABCBDAB’,b = ‘BDCABA’,最长公共子序列: BCBA
- 尽管个数不是唯一的,可能会有两个以上, 但是长度一定是唯一
- 有些时候,动态规划其中的子问题很复杂,不要被弄得迷茫了
def lcs(a, b):
lena = len(a) # a序列的长度
lenb = len(b) # b序列的长度
c = [[0 for i in range(lenb + 1)] for j in range(lena + 1)] # 存放两个列表最长公共子序列的长度
flag = [[0 for i in range(lenb + 1)] for j in range(lena + 1)] # 帮助构造最优解
# 首先由左至右计算c的第一行, 然后计算第二行,以此类推
for i in range(lena):
for j in range(lenb):
if a[i] == b[j]: # 如果a[i]等于b[j]是LCS的一个元素
# 因为第一行与第一列位构造的表头都是0, 因此i+1,j+1,从第二行第二列那个0开始算
c[i+1][j+1] = c[i][j] + 1
flag[i+1][j+1] = 'ok' # flag位置显示ok,是LCS中的一个元素
elif c[i+1][j] > c[i][j+1]: # 如果c表中LCS中记录的长度,当左边的值大于其上方的值
c[i+1][j+1] = c[i+1][j] # 将左边的LCS长度的值赋值给当前位置
flag[i+1][j+1] = 'left' # 箭头号指向左边,表示从左边赋值来的
else:
c[i+1][j+1] = c[i][j+1] # 如果c表中LCS中记录的长度,当上边的值大于其左边的值
flag[i+1][j+1] = 'up' # 箭头号指向上方up,表示从上边继承下来的
return c, flag
def printLcs(flag, a, i, j):
if i == 0 or j == 0:
return
if flag[i][j] == 'ok':
printLcs(flag, a, i - 1, j - 1)
print(a[i - 1], end='')
elif flag[i][j] == 'left':
printLcs(flag, a, i, j - 1)
else:
printLcs(flag, a, i - 1, j)
a = 'ABCBDAB'
b = 'BDCABA'
c, flag = lcs(a, b)
for i in c:
print(i)
print('')
for j in flag:
print(j)
print('')
printLcs(flag, a, len(a), len(b))
print('')
'''
最终结果:
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]
[0, 0, 0, 0, 0, 0, 0]
[0, 'up', 'up', 'up', 'ok', 'left', 'ok']
[0, 'ok', 'left', 'left', 'up', 'ok', 'left']
[0, 'up', 'up', 'ok', 'left', 'up', 'up']
[0, 'ok', 'up', 'up', 'up', 'ok', 'left']
[0, 'up', 'ok', 'up', 'up', 'up', 'up']
[0, 'up', 'up', 'up', 'ok', 'up', 'ok']
[0, 'ok', 'up', 'up', 'up', 'ok', 'up']
BCBA
Process finished with exit code 0
'''
我去旅行,是因为我决定了要去,并不是因为对风景的兴趣
- 不惋惜,不呼唤,我也不啼哭。一切将逝去,如苹果花丛的薄雾。金黄的落叶堆满心间,我已不再是青春少年
- 胆小鬼连幸福都会害怕,碰到棉花都会受伤,有时还被幸福所伤
- 从卖气球的人那里,每个孩子牵走一个心愿,祝大家在新的一年里好运连连,万事顺遂!
- 热爱、可抵岁月漫长!